Задача 2.2.1
Решение
о покупке автомобиля. Рассмотрим простую
ситуацию: человек, располагающий запасом
денег W решает,
приобрести ли автомобиль по цене p,
его полезность измеряется в деньгах и
денежная оценка факта наличия у него
автомобиля для человека составляет 
(итого при покупке автомобиля его выигрыш
составит W
- p
+
,
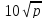а в отсутствие автомобиля просто
измеряется размером богатства W).
Представьте ситуацию в виде дерева
решений. Найдите граничное значение
цены автомобиля, при котором человеку
безразлично — покупать автомобиль или
нет.
Решение:
Дерево решений состоит из следующих компонент:
• одна начальная вершина;
• две конечные вершины;
• две ветви, исходящие из начальной вершины;
• в каждой из конечных вершин указываются выигрыши.
Человеку безразлично
– покупать автомобиль или нет, если
выигрыши в конечных вершинах совпадают:
,
т.е.
.
Решаем это уравнение:
Следовательно,
если цена автомобиля равна
,
то выигрыши в конечных вершинах дерева
решений получаются одинаковыми, и
человеку безразлично – покупать
автомобиль или нет.
Задача 2.2.6
Задача
выбора количества потребляемых товаров
при бюджетном ограничении. Потребитель
распределяет весь свой доход между
потреблением некоторого обычного товара
в количестве 
,
покупая его по цене p руб.
за единицу, и потреблением всех остальных
товаров, рассматривая его, как денежный
остаток, который он не тратит на первый
товар, — 
.
Полезность потребителя задана функцией 
,
а множество доступных альтернатив
задано бюджетным множеством в виде 
,
где R —
весь доход потребителя. Найдите
оптимальный выбор потребителя в
зависимости от параметров: 
.
Являются ли предпочтения потребителя
рациональными (поясните)? Каков
содержательный смысл двойственной
оценки бюджетного ограничения в такой
задаче?
Решение:
Предпочтения потребителя рациональны: предпочитает такой план расходов (x,z), при котором u больше. А если два плана приводят к одинаковой u, потребителю безразлично, какой выбрать.
Запишем данную задачу выпуклого программирования в виде
Так
как
возрастающая функция, мы можем искать
только такие
,
которые обращают первое неравенство в
равенство. Если бы максимум u
достигался при другом
,
то при большем
,
все еще удовлетворяющем первому
неравенству (бюджетному ограничению),
и том же z,
u
будет еще больше, противоречие.
Математически это записывается
неравенством
при
всех
таких, что
Таким образом, надо максимизировать
в области
Найдем производную по z
она может обратиться
в 0 только при
,
это неотрицательная величина только
при
,
и тогда
Напротив,
при
производная отрицательна при всех
неотрицательных z,
а u
принимает свое наибольшее значение при
,
при этом выводим, что оптимальные
Рассмотрим двойственную задачу. Переменная у этой задачи показывает, на сколько денежных единиц изменится полезность при оптимальном плане распределения бюджета потребителя при увеличении бюджета на 1 ден.ед., если денежную единицу выбрать очень мелкую.
Преобразуем задачу к виду
Но,
как уже показано при решении исходной
задачи, здесь
может быть только нулем, и это упростит
дальнейшие формулы.
Решая эту систему, получаем
,
таким образом, при R>1
на единицу прироста бюджетного ограничения
приходится единица прироста функции
полезности
Во втором случае, при R<1, по условию дополняющей нежесткости, ограничение z=0 является активным. Переменная у является отношением длин синего и красного векторов – проекций градиентов на ось х
Решаем систему и получаем
Таким образом, при R < 1 малый прирост R приводит к в 1/R раз большему приросту функции полезности.
Ответ: оптимальный выбор потребителя при R<1
,
Иначе
