
- •Дискретная математика Программа, методические указания и задания для контрольной работы
- •Удк 51(0.75)
- •Оглавление
- •Программа курса Теория множеств
- •Комбинаторика
- •Алгебра логики
- •Конечные автоматы
- •Рекомендуемая литература
- •Правила выполнения и оформления контрольной работы
- •Задачи для контрольной работы Задачи 1-20
- •Задачи 21-40
- •Задачи 41-60
- •Задачи 61-70
- •Задачи 71-80
- •Задачи 81-100
- •Задачи 101-120
- •Задачи 121-140
- •Задачи 141-160
- •Методические указания для выполнения контрольной работы
- •Теория множеств
- •Комбинаторика
- •Алгебра логики
- •Граф на рисунке имеет две компоненты связности.
- •630102, Г. Новосибирск, ул. Кирова, 86.
Методические указания для выполнения контрольной работы
Теория множеств
Под множеством понимают любую совокупность объектов. Сами объекты, из которых состоит множество, называются элементами. Множества обозначают прописными буквами (А, В, С и т.д.), а их элементы – строчными (например: x,y,z). Если элемент x принадлежит множеству А, то пишут x A. Запись x A означает, что элемент x не принадлежит множеству А. Множество, не содержащее элементов, называется пустым множеством и обозначается символом . Для числовых множеств будем использовать следующие обозначения:
N - множество натуральных чисел,
Z – множество целых чисел,
R – множество действительных чисел.
Способы задания множеств
Множества могут быть заданы тремя основными способами.
Перечислением элементов множества. Например, А={2,7,10}.
Указанием характерных свойств элементов множества. Например, А={x R| x>0} – множество всех положительных чисел.
Описанием способа построения. Например, А= {5i | i=1,2,…n}.
Отношения между множествами
Два множества равны, если они состоят из одних и тех же элементов. Равенство множеств обозначается какА=В. Если множества не равны, то пишутАВ.
Если каждый элемент множества А является элементом множества В, то пишут А В (А является подмножеством множества В). Для числовых множеств выполняется NZR. Считается, что А для любого множества А.
Теорема. Множество А равно множеству В тогда и только тогда, если А В и В А.
Данная теорема дает метод доказательства равенства двух множеств.
Если все рассматриваемые множества являются подмножествами более широкого множества U, то множество U называется универсальным множеством.
Диаграммы Венна
Д ля
повышения наглядности представления
множеств используют диаграммы Венна в
виде кругов, ограничивающих области,
которым ставятся в соответствие элементы
тех или иных множеств. Например:
ля
повышения наглядности представления
множеств используют диаграммы Венна в
виде кругов, ограничивающих области,
которым ставятся в соответствие элементы
тех или иных множеств. Например:
Если множества не имеют общих элементов, то их изображают непересекающимися кругами. В противном случае, круги пересекаются. Универсальное множество изображают в виде прямоугольника.
Операции над множествами
Декартовым
произведением
множеств А1, А2, …, Аn
называется множество всех упорядоченных
наборов (x1 ,x2, … xn)
таких, что
![]() приi=1,2,…,n.
Декартово
произведение обозначается
приi=1,2,…,n.
Декартово
произведение обозначается
![]() .
В частности,
.
В частности,![]()
Н апример,
пусть имеются множестваA={1,2},
B={2,3,4}.
Тогда
апример,
пусть имеются множестваA={1,2},
B={2,3,4}.
Тогда
![]()
Объединением
множеств А
и В
называется множество
![]()
Пересечением
множеств А и В называется множество
![]()
Разностью
множеств А и В называется множество
![]()
Симметрической
разностью
множеств А и В называется множество
![]() .
.
Дополнением
множества А называется множество
![]() .
.
Введенные понятия заштрихованы на диаграммах темным цветом.
Свойства операций над множествами
Введенные операции под множествами обладают следующими свойствами.
Коммутативность
![]()
Ассоциативность
![]()
Дистрибутивность
![]()
Идемпотентность
![]()
Двойственность (законы де Моргана)
![]()
Операции с пустым множеством
![]()
![]() =
=
Операции с универсальным множеством
![]()
Операции с дополнением
![]()
Определение разности через пересечение
![]()
Поглощение
![]()
На основании свойств 1–10 можно получить новые свойства и равенства.
Пример 1.1. Доказать, что верно равенство
![]()
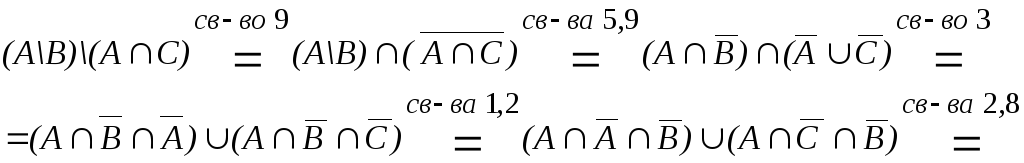
=(![]()
![]()
=![]()
Отношения на множествах
Бинарным отношением R на множествах А и В называется любое подмножество декартова произведения множеств А и В.
![]()
Если элементы x и y множеств А и В находятся в отношении R, то пишут (x,y)R или xRy. Если А=В, то R называется бинарным отношением на А.
Бинарное отношение можно задать указанием всех элементов, входящих в соотношение, или графически. Основу графического представления бинарного отношения составляет прямоугольная система координат, где по одной оси откладываются элементы одного множества, а по второй – другого. Пересечения координат образуют точки, обозначающие элементы декартова произведения.
Пример 1.2 Рассмотрим множества A={1,2,3,4,5,6}, B={1,2,3}. Определим на этих множествах отношение RAB.
R={(x,y) | x делится на y}.
R можно представить графически следующим образом:
С вяжем
с каждым бинарным отношениемR
между
множествами A
и B
два множества – область определения
R
и
множество значений R.
Они определяются следующим образом:
вяжем
с каждым бинарным отношениемR
между
множествами A
и B
два множества – область определения
R
и
множество значений R.
Они определяются следующим образом:
R={x| (x,y)R для некоторого y},
R={y| (x,y)R для некоторого x}.
Пример 1.3 Пусть на множестве A={1,2,3,4,5} задано отношение R: R={(x,y) | остаток от деления y на x равен 1}.
Тогда R={(5,1), (4,1), (3,1), (2,1), (2,3), (2,5), (3,4), (4,5)},
R={2,3,4,5}, R={1,3,4,5}.
Пусть имеются множества A, B, C и отношения RAB, PBC. Определим отношение SAC следующим образом: оно действует из A в B посредством R, а затем из B в C посредством P. Такое отношение называется составным и обозначается S=P◦R.
S={(x,y) | zB, для которого выполнено (x,z)R, (z,y)P}.
П ример1.4
Пусть
A={1,2,3,4},
на множестве A
определим
два отношения:
R={(x,y)
| 2x
y}
и P={(x,y)
| x+3y
делится
на 2}.
Найдем
графические представления отношений
R,
P, S
=
P◦R.
ример1.4
Пусть
A={1,2,3,4},
на множестве A
определим
два отношения:
R={(x,y)
| 2x
y}
и P={(x,y)
| x+3y
делится
на 2}.
Найдем
графические представления отношений
R,
P, S
=
P◦R.
Найдем области определения и области значений для всех отношений.
R={1,2}, R={2,3,4}, P={1,2,3,4}, P={1,2,3,4}, S={1,2}, S={1,2,3,4}.
Бинарное
отношение R
на множестве
А
называется рефлексивным,
если для всякого
![]() выполняется
выполняется![]() .
.
Бинарное отношение R на множестве А называется симметричным, если из того, что выполняется xRy следует выполнение yRx.
Бинарное отношение R на множестве А называется антисимметричным, если из выполнения xRy и yRx следует, что x=y.
Бинарное отношение R на множестве А называется транзитивным, если из выполнения xRy и yRz следует выполнение xRz.
Рефлексивное, симметричное и транзитивное отношение R на множестве A называется отношением эквивалентности.
Рефлексивное, антисимметричное и транзитивное отношение R на множестве А называется частичным порядком.
Пример
1.5.
Определим отношение R
на множестве
натуральных чисел следующим образом:
![]() (a+2b делится
на 3).
(a+2b делится
на 3).
Это
отношение является рефлексивным, т.к.
![]()
Отношение R симметрично.
![]() .
Для того, чтобы проверить выполнение
bRa,
необходимо показать, что
.
Для того, чтобы проверить выполнение
bRa,
необходимо показать, что
![]()
![]() ,
,
![]() выполнено.
выполнено.
Отношение
R
не является
антисимметричным, т.к. 6R3,
3R6,
но
![]() .
.
Проверим,
что R
– транзитивно.
![]() ,
,
![]() .
Для того, чтобы проверить выполнение
aRc,
необходимо показать, что
.
Для того, чтобы проверить выполнение
aRc,
необходимо показать, что
![]() .
.
![]()
aRc выполнено.
