
ДМ_гл2_DO
.docГлава 2 Элементы комбинаторики
Комбинаторика – раздел математики, посвященный решению задач выбора и расположения элементов некоторого обычного множества в соответствии с заданными правилами. Каждое такое правило определяет способ построения некоторой конструкции из элементов исходного множества, называемой комбинаторной конфигурацией. Простейшими примерами комбинаторных конструкций являются перестановки, размещения, сочетания и разбиения, рассматриваемые ниже. Вычисления на дискретных математических структурах – комбинаторные вычисления – требуют комбинаторного анализа для установления свойств и оценки применимости алгоритмов.
-
Агенство недвижимости, база данных. Запись – пара (предложение, спрос). Найти варианты обмена (т.е. такие пары, где первая компонента одной совпадает со второй компонентой другой). Простейший вариант поиска – «лобовой», трудоемкость n(n–1)/2. Если на одну проверку нужна 1 миллисекунда, то при n = 100 потребуется около 5 секунд, при n=100 000 – 5106 сек, т.е. около 1389 часов. Непригодный алгоритм!!!
-
Комбинаторные задачи и основные принципы
-
Комбинаторные задачи
Во многих практических задачах возникает необходимость подсчитать количество возможных комбинаций объектов, удовлетворяющих определенным условиям. Такие задачи называются комбинаторными.
-
1. Некто одновременно бросает несколько игральных костей и подсчитывает сумму очков на верхних гранях. Спрашивается – сколько существует различных вариантов результата? 2. В районном городе проживает некоторое количество людей. Открывается телефонная станция. Спрашивается – сколько должно быть цифр в телефонном номере, чтобы всем абонентам хватило различных номеров, да еще и остались запасные с перспективой дальнейшего роста населения?
Такие и подобные им задачи относятся к классу комбинаторных задач.
Среди всего многообразия таких задач есть ряд наиболее часто встречающихся, для которых известны способы подсчета.
Для формулировки и решения комбинаторных задач используются различные модели комбинаторных конфигураций. Рассмотрим две наиболее популярные.
-
Дано n предметов. Их нужно разместить по m ящикам так, чтобы выполнялись заданные ограничения. Сколькими способами это можно сделать?
-
Дано множество функций F : X Y, где |X| = n, |Y| = m, X = {1,2,…,n} (предметы – элементы множества X – перенумерованы, т.е. можно считать номер отличительным признаком предмета). Без ограничения общности можно считать, что элементы множества Y также перенумерованы: Y = {1,2,…,m}, F = [F(1),…,F(n)], 1 F(i) m. Сколько существует функций, удовлетворяющих заданным ограничениям?
Наиболее часто соответствие конфигураций 1-го и второго типа очевидно, поэтому анализ проблем и вывод формул можно проводить на любом языке.
-
Основные комбинаторные принципы
Утверждение 2.1 Если множества A и B не пересекаются и содержат по m и n элементов соответственно, то множество AB содержит m + n элементов: для множеств A и B | AB=: |A B| = |A| + |B|.
-
(о произведении множеств):
Для любых множеств A и B |AB|=|A||B|.
Доказательство: Множество C = AB состоит из упорядоченных пар вида (a,b), aA, bB. Пуст8ь |A| = m, |B| = n. Первый компонент упорядоченной пары можно выбрать m способами. Если его зафиксировать, то второй элемент можно выбрать n способами. Следовательно, всего имеется mn различных упорядоченных пар.
Правило суммы (комбинаторный принцип сложения) Если объект A можно выбрать m способами, а объект B, отличный от , n способами, причем и нельзя выбрать одновременно, то осуществить выбор «либо , либо » можно m+n способами.
-
Пусть в киоске имеется 5 различных книг по математике и 7 – по физике. Если студент может купить только одну книгу, то у него есть 5 вариантов выбора первой книги и 7 вариантов – второй, т.е. 12 вариантов.
Правило произведения (комбинаторный принцип умножения) Если объект A можно выбрать m способами, а после каждого такого выбора можно выбрать n способами объект B, отличный от , то выбор обоих объектов и в указанном порядке можно осуществить mn способами.
-
Пусть в салоне связи имеется 50 различных моделей сотовых телефонов и по три вида чехлов для каждой модели. Сколькими способами можно выбрать телефон и чехол к нему? Очевидно: Выбрав телефон (50 способов), можно 3 способами выбрать чехол, т.е. всего 503=150 вариантов.
Сравнивая утверждение 2.1 и теорему 2.1 с правилами суммы и произведения, заметим, что в них речь идет об одних и тех же закономерностях, хотя и используются различные формулировки. Очевидным образом эти правила распространяются на случай большего количества множеств.
-
Контрольные вопросы
-
Какие задачи относят к классу комбинаторных?
-
В чем состоит комбинаторный принцип сложения?
-
Как формулируется принцип умножения? Приведите пример.
-
Комбинаторные конфигурации
-
Перестановки и подстановки
Пусть дано множество M = {a1,a2,…,an}. Перестановкой элементов множества M называется любой упорядоченный набор из n различных элементов множества M.
Перестановки различаются только порядком входящих в них элементов.
Перестановка элементов множества M может быть задана посредством функции подстановки. Будем определять подстановку как биекцию : M M и задавать ее с помощью матрицы, состоящей из двух строк.
Пусть множество
M = {1,2,…,n},
а (k) =sk,
1 sk n,
k=1,…,n,
{s1,s2,…,sn} = {1,2,…,n}.
Тогда матрица подстановки
будет иметь вид: [] ![]() .
Очевидно, что перестановка столбцов в
этой матрице не меняет задаваемой ею
подстановки.
.
Очевидно, что перестановка столбцов в
этой матрице не меняет задаваемой ею
подстановки.
Если
заданы две подстановки
и своими матрицами
[] и [],
то их произведение
определяется следующим образом. В
матрице [] столбцы
переставляются так, чтобы ее первая
строка совпала со второй строкой матрицы
[]:
 .
В итоге получится:
.
В итоге получится:
[][] = ![]()
 =
=![]() .
.
-
Если заданы подстановки [] =
 ,
[] =
,
[] =  ,
то [] =
,
то [] = 
 =
= 
 =
=  .
.
Тождественная подстановка – это такая подстановка e, что e(x)=x x.
-
[e] =
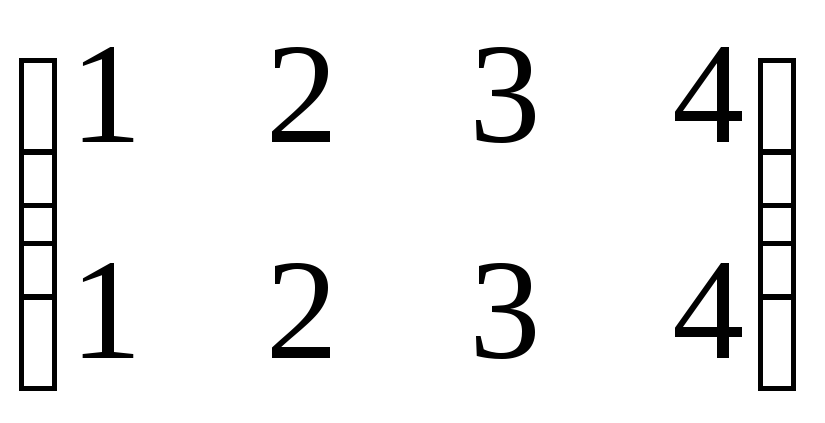 .
.
Обратная подстановка – это обратная функция, которая всегда существует (подстановка является биекцией). Для получения таблицы обратной подстановки нужно поменять местами строки таблицы исходной подстановки.
-
Для подстановки [] =
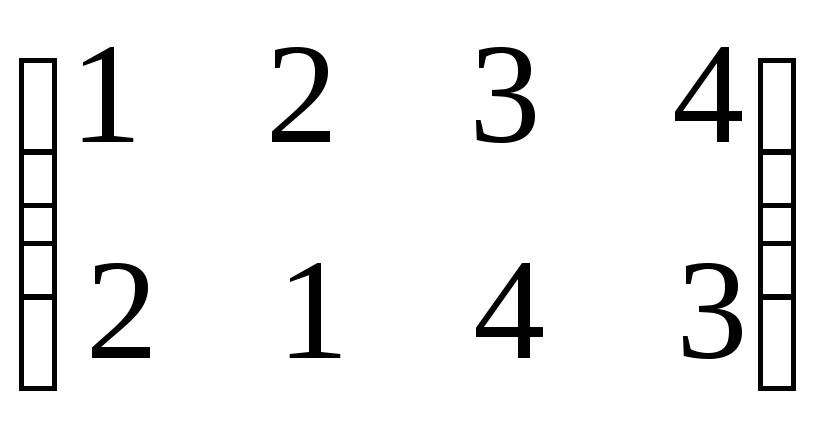 [–1] =
[–1] =  .
.
Подстановка называется циклом длины r, если матрицу [] перестановкой столбцов можно привести к виду:
 ,
т.е. первые r элементов
сменяют друг друга, а остальные неподвижны:
(si) = si+1,
для 1 i r –1
и (sr) = s1.
,
т.е. первые r элементов
сменяют друг друга, а остальные неподвижны:
(si) = si+1,
для 1 i r –1
и (sr) = s1.
-
Подстановка с матрицей [] =
 =
= является циклом (2 5 3 6), а
подстановка с матрицей [] =
является циклом (2 5 3 6), а
подстановка с матрицей [] =  циклом не является, т.к. из нее можно
выделить два цикла (1 4) и (2 5 6 3).
циклом не является, т.к. из нее можно
выделить два цикла (1 4) и (2 5 6 3).
Утверждение 2.2 Каждую подстановку можно однозначно (с точностью до порядка сомножителей) представить в виде произведения независимых циклов.
В примере
2.7 [] = (2 5 3 6),
[] = ![]() = (1 4)(2 5 6 3).
= (1 4)(2 5 6 3).
Двухэлементный цикл (i j) называется транспозицией. При транспозиции меняются местами только i-й и j-й элементы, а остальные сохраняют свое положение.
П одстановку
удобно изображать графически,
соединяя стрелками элементы x
и (x):
одстановку
удобно изображать графически,
соединяя стрелками элементы x
и (x):
![]() .
.
Используя только транспозиции, можно выполнить сортировку множества в определенном порядке (например, в лексикографическом). Известный алгоритм сортировки, основанный на этом принципе, на каждом шаге осуществляет перестановку только двух соседних элементов и носит название «пузырьковой сортировки».
Число перестановок объема n принято обозначать как Pn.
Утверждение 2.3 Число всех перестановок множества M (|M| = n) равно n!
Действительно, на первое место в n-ке можно поставить любой из n элементов множества, на второе место – любой из (n–1) оставшихся, и т.д. Для последнего места остается единственный элемент. Поэтому получаем: Pn = n(n–1)(n–2)…21 = n!
-
Сколькими способами можно расставить на полке 6 томов книг? Это можно осуществить P6 = 6! = 720 способами.
-
Понятие выборки
Пусть дано множество M = {a1, a2, a3, ..., an}, m n. Набор, состоящий из m элементов множества М, называется выборкой объема m из n элементов.
Выборки классифицируются следующим образом:
-
По критерию повторяемости элементов: С возвращением объема (с повторениями) и без возвращения объема (без повторений).
-
По критерию упорядоченности:
Упорядоченные (размещения) и неупорядоченные (сочетания).
-
В ящике n≤10 нумерованных шаров, один достают, записывают номер и бросают обратно. Так делают три раза. Сколько разных трехзначных чисел может получиться? Для подсчета нужны размещения с повторениями.
-
Размещения и сочетания без повторений
Размещениями из n элементов по m называются упорядоченные выборки без повторений элементов множества, которые отличаются одна от другой либо составом элементов, либо порядком их расположения. Размещение можно рассматривать как разнозначную функцию f:{1,2,…,m}M, для которой f(j)=aij.
Тогда числу размещений
из n элементов по m соответствует
число инъективных функций или число
всех возможных способов разместить n
предметов по m позициям
(«ящикам»), не более чем по одному в
«ящик». Это число будем обозначать
![]() =A(n,m)
(иногда обозначают P(n,m)).
=A(n,m)
(иногда обозначают P(n,m)).
-
Пусть дано множество M={1,2,3,4,5}. Тогда размещениями из 5 элементов по 2 будут, в частности, выборки (1,2), (2,1), (2,4), (4,2) и т.п.
-
 = n(n–1)(n–2)…(n–m+1).
= n(n–1)(n–2)…(n–m+1).
Доказательство: Размещение m
элементов из n имеющихся
будем рассматривать как заполнение
некоторых m позиций
элементами множества M.
Для первой позиции существует n
различных способов. После того, как
первая позиция заполнена, элемент для
второй позиции можно выбрать (n–1)
способами (комбинаторный принцип
умножения). Если процесс продолжить, то
после заполнения позиций с 1-й по (m–1)-ю
останется (n–m+1)
способ для последней, m-й
позиции. Перемножив эти числа, получим
формулу для
![]() .
.
Сочетаниями без повторений из n элементов по m называются неупорядоченные выборки без повторений элементов множества, которые отличаются одна от другой только составом элементов. Иными словами, это любые подмножества исходного множества, состоящие из m элементов.
-
Пусть дано множество M={1,2,3,4,5}. Тогда сочетаниями из 5 элементов по 2 будут выборки (1,2), (2,4), (5,2) и т.п. (Здесь (2,4)~(4,2)…)
Число сочетаний без повторений будем
обозначать
![]() или C(n,m).
или C(n,m).
![]() .
.
Формула
для числа размещений из n
элементов по m была
получена ранее. Если объединить
размещения, отличающиеся только порядком
элементов и совпадающие по составу, в
классы эквивалентности, то получим, что
мощность каждого из таких классов m!
Тогда число сочетаний будет определяться
как C(n,m)=
![]() .
.
-
На тренировках занимаются 8 баскетболистов. Сколько разных пятерок может быть образовано тренером? Т.к. при образовании пятерки важен только ее состав, то достаточно определить
 пятерок.
пятерок.
-
Размещения и сочетания с повторениями
Размещениями с повторениями (или упорядоченными выборками с возвращениями) из n элементов по k называются упорядоченные наборы из k элементов множества M, в которых элементы множества могут повторяться.
-
Пусть дано множество M={1,2,3,4,5}. Тогда размещениями с повторениями из 5 элементов по 2 будут (1,1), (1,2), (2,1), (2,2), …,(5,1) и т.п. – любые упорядоченные пары из 2 элементов множества М.
Количество всех размещений с повторениями
обозначим
![]() =Â(n,k).
Поскольку в таком наборе из k
элементов на каждом из k
мест может стоять любой из n
элементов исходного множества, число
размещений с повторениями равно
nn…n = nk.
=Â(n,k).
Поскольку в таком наборе из k
элементов на каждом из k
мест может стоять любой из n
элементов исходного множества, число
размещений с повторениями равно
nn…n = nk.
![]() . (2.1)
. (2.1)
-
а) Сколько различных трехзначных чисел можно составить из цифр 1, 2, 3, 4, 5? б) А при условии, что ни одна цифра не повторяется? Составить разные числа можно:
 способами (размещения с повторениями).
Если ни одна цифра не должна повторяться,
то таких способов будет
способами (размещения с повторениями).
Если ни одна цифра не должна повторяться,
то таких способов будет
 (размещения без повторений).
(размещения без повторений).
В отличие от выборок без повторений, количество выбираемых объектов может быть больше, чем количество типов, т.е. может быть k n. Если вернуться к примеру 2.12 (а), то можно рассматривать и 10-разрядные числа.
-
(о мощности множества P(M) )
Для конечного множества M |2M| = 2|M|.
Доказательство:
Пусть конечное множество M состоит из n элементов, M = {x1, …, xn}. Сопоставим каждому его подмножеству двоичный вектор длины n. Если xi входит в подмножество, то на i-м месте в этом векторе будет стоять 1, иначе – 0. Поскольку каждая компонента вектора может принимать только значения 0 или 1, а всего таких компонент n, то число различных векторов составит 2n.
Следствие:
Можно сгенерировать все подмножества конечного множества M, перечислив некоторым способом все наборы из нулей и единиц длины n.
Можно выполнять такую генерацию различными способами (например, все наборы с одной «1», все с двумя «1», …). Это можно сделать наиболее эффективно, используя т.н. бинарный код Грея. Алгоритм построения бинарного кода Грея позволяет генерировать последовательность всех подмножеств n-элементного множества таким образом, что каждое последующее подмножество получается из предыдущего добавлением или удалением единственного элемента. Подробно этот алгоритм рассматривается при выполнении лабораторной работы.
Определим отношение эквивалентности на множестве размещений с повторениями из n элементов по k: (a1,a2,…,ak) ~ (b1,b2,…,bk) cM число элементов ai = c совпадает с числом элементов bj = c.
Тогда сочетанием с повторениями из n элементов по k или неупорядоченной выборкой с возвращениями из n элементов по k является множество, которое состоит из элементов, выбранных k раз из множества M, причем один и тот же элемент допускается выбирать повторно.
-
В примере с множеством M={1,2,3,4,5} сочетания с повторениями из 5 элементов по 2 будут отличаться от размещений тем, что одинаковые по составу наборы будут независимо от порядка элементов в них считаться эквивалентными: (1,1), (1,2)~(2,1), (2,2), (5,2) и т.п.
При рассмотрении выборок с повторениями число n более наглядно трактуется как количество имеющихся в наличии типов объектов, а k – количество непосредственно выбираемых объектов. Раз объекты выбираются с повторениями, неважно, каково их реальное количество для каждого из типов. Можно считать их неисчерпаемыми.
Число
всех сочетаний с повторениями обозначается
![]() =Ĉ(n,k)
и вычисляется по формуле: Ĉ(n,k)=
=Ĉ(n,k)
и вычисляется по формуле: Ĉ(n,k)=![]() (2.2)
(2.2)
-
Пусть в кондитерской продается 10 различных видов пирожных. (n=10 – число типов). Сколькими способами можно купить 12 пирожных? (k=12). Ĉ(10,12)=C(10+12–1,12)=C(21,12)=21!/(12! (10–1)!)= 21!/(12! 9!).
-
Контрольные вопросы
-
Что такое подстановка? Всегда ли существует обратная подстановка?
-
Какая перестановка элементов множества {1,2,3,4} задана функцией подстановки
 ?
Является ли эта подстановка циклом?
?
Является ли эта подстановка циклом? -
Что такое транспозиция? В каком алгоритме она используется?
-
Как называется упорядоченная выборка без возвращения объема и по какой формуле вычисляется число различных таких выборок?
-
Сколько различных двузначных чисел можно получить, используя множество {1,2,3,4,5}? Как изменится результат, если цифры в числе не повторяются? Какая выборка (и формула) используется в каждом случае?
-
Сколько двузначных чисел с различной суммой цифр можно получить, используя множество {1,2,3,4,5}? Цифры в числе должны быть разными. В чем отличие от предыдущей задачи? Сочетания или размещения нужно использовать?
-
В чем отличие сочетаний с повторениями от остальных конфигураций?
-
Пусть в киоске есть три вида открыток. Сколькими способами можно купить 6 открыток? А три открытки? Какая конфигурация используется?
-
Биномиальные коэффициенты
Число
сочетаний C(n,k)=![]() – число различных k-элементных
подмножеств n-элементного
множества – встречается в формулах
решения многих комбинаторных задач.
Например, для определения числа
подмножеств n-элементного
множества, удовлетворяющих некоторому
условию, задача разбивается на составные
части: рассматриваются отдельно
1-элементные подмножества, 2-элементные
и т.д., затем результаты складываются.
– число различных k-элементных
подмножеств n-элементного
множества – встречается в формулах
решения многих комбинаторных задач.
Например, для определения числа
подмножеств n-элементного
множества, удовлетворяющих некоторому
условию, задача разбивается на составные
части: рассматриваются отдельно
1-элементные подмножества, 2-элементные
и т.д., затем результаты складываются.
Числа
![]() =
=![]() называются биномиальными коэффициентами.
называются биномиальными коэффициентами.
-
Свойства биномиальных коэффициентов
-
Число
 обладает следующими свойствами:
обладает следующими свойствами:
-
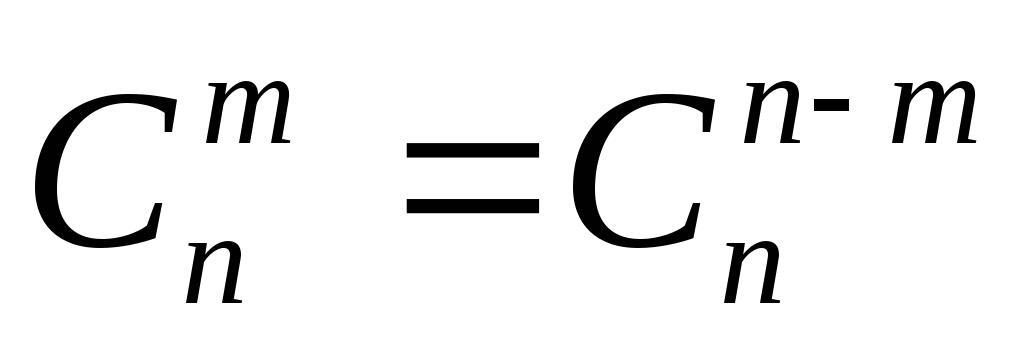 ; 2.
; 2.  ; 3.
; 3. 
Доказательство.
1.
![]()
![]() =
=![]() =
=![]()
![]()
2.
![]() =
=
![]() =
=
![]()
![]() =
=
![]() =
=
![]() = =
= =![]() =
=
![]() =
=
![]() .
.
3.![]()
![]()
![]() =
=
![]() =
=
![]() =
=
![]() =
=![]() =
=
![]()
![]() .
.
-
(Бином Ньютона) При любых x, y R (x+y)n =
 .
.
Доказательство: По индукции.
База:
n =1:
(x+y)1 = x+y = 1x1y0+1x0y1=![]() x1y0+
x1y0+
![]() x0y1=
x0y1=
![]() .
.
Индукционный
переход:
(x+y)n=(x+y)n–1(x+y)
= x![]() +
y
+
y![]() =
=![]() x1yn–1+
x1yn–1+![]() x2yn–2+
…+
x2yn–2+
…+![]() xn–1y1+
xn–1y1+![]() xny0+
xny0+![]() x0yn
+
x0yn
+![]() x1yn–1+
x1yn–1+![]() x2yn–2
+
…+
x2yn–2
+
…+![]() xn–1y1=
(
xn–1y1=
(![]() +
+![]() )·x1yn–1+
(
)·x1yn–1+
(![]() +
+![]() )·x2yn–2+…+(
)·x2yn–2+…+(![]() +
+![]() )·xn–1y1+
(
)·xn–1y1+
(![]() xny0+
xny0+
![]() )·x0yn
= |
)·x0yn
= |![]() =
=![]() ;
;
![]() =
=![]() |
=
|
=![]() x1yn–1+
x1yn–1+![]() x2yn–2
+…+
x2yn–2
+…+![]() xn–1y1+
xn–1y1+![]() xny0+
xny0+
![]() x0yn
=
x0yn
=
![]() .
.
Следствие
1. 2n =
![]() .
Действительно, 2n = (1+1)n =
.
Действительно, 2n = (1+1)n = ![]() .
.
Следствие
2.
![]() .
Действительно,
0= (–1+1)n =
.
Действительно,
0= (–1+1)n = ![]() .
.
1.
![]() ; 2.
; 2.
![]() (Тождество Коши).
(Тождество Коши).
Доказательство:
1. ![]() 0·
0·![]() +1·
+1·![]() +2·
+2·![]() +…+(n–1)·
+…+(n–1)·![]() +n·
+n·![]() =(0+n)·
=(0+n)·![]() +(1+n–1)·
+(1+n–1)·![]() +
(2+n–2)·
+
(2+n–2)·![]() +…=
n/2·
+…=
n/2·![]()
![]() .
.
2.
![]() – это число способов выбрать k
предметов из m+n
предметов. Их можно выбирать в два
приема: сначала выбрать i
предметов из первых n
предметов,
а затем недостающие k–i
предметов – из оставшихся m
предметов.
Отсюда общее число способов выбрать k
предметов составляет
– это число способов выбрать k
предметов из m+n
предметов. Их можно выбирать в два
приема: сначала выбрать i
предметов из первых n
предметов,
а затем недостающие k–i
предметов – из оставшихся m
предметов.
Отсюда общее число способов выбрать k
предметов составляет
![]() .
.
