Спектральные характеристики дискретных сигналов
Спектральные характеристики дискретизированного сигнала U1(n) рассчитываются по формуле:
.
На частотах:
ω = 0
ω = π/4Т=625Гц;
ω = π/2Т=1250Гц;
ω = 3π/4Т=1875Гц
ω = π/Т=2500Гц
ω = π/4Т
ω = π/2Т
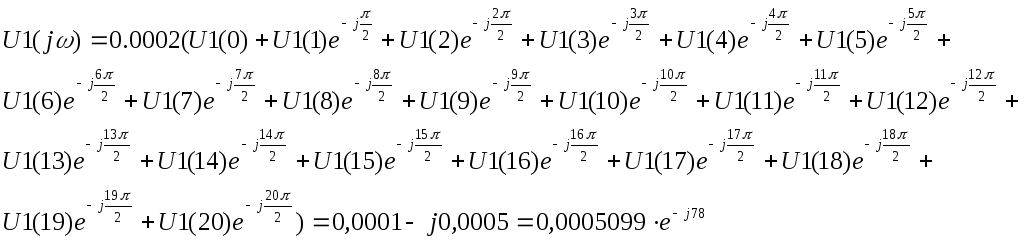
ω = π/Т
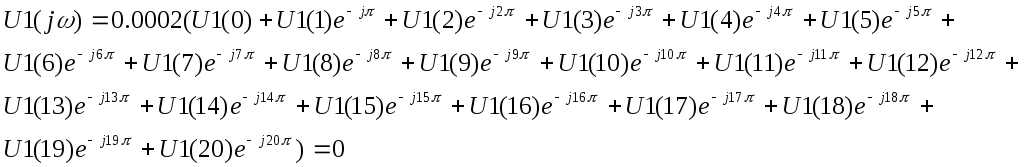
ω = 0
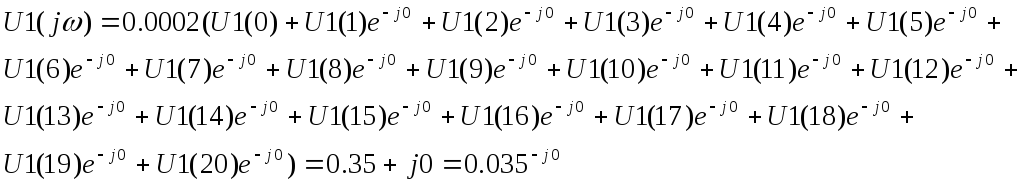
ω = 3π/4Т
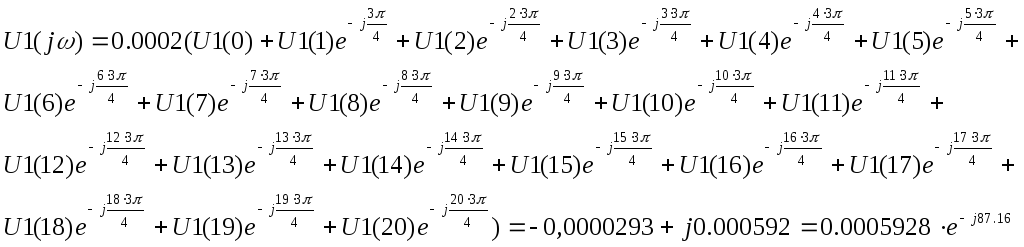
Спектральная характеристика дискретного сигнала:
ω
U1(jω)|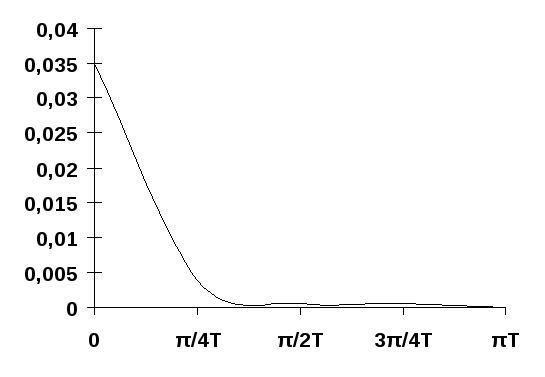
Спектральные характеристики дискретизированного сигнала U2(n) рассчитываются по формуле:
.
На частотах:
ω = 0
ω = π/4Т
ω = π/2Т
ω = 3/4Т
ω = π/Т
ω = π/4Т
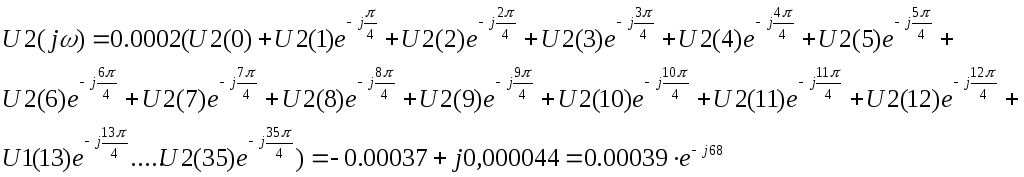
ω = π/2Т
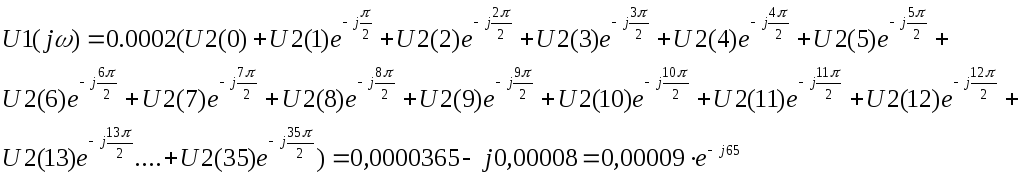
ω = π/Т
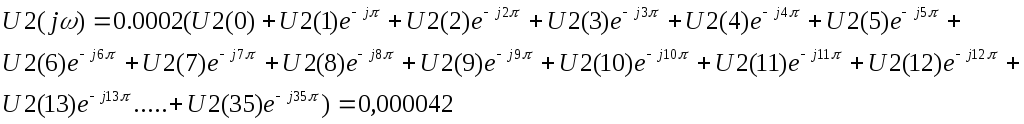
ω = 0
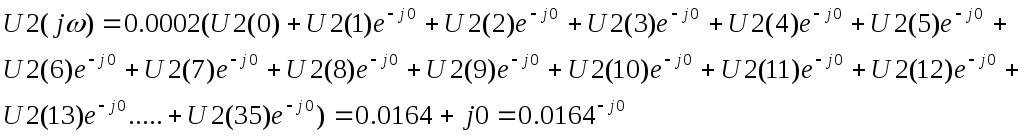
ω=3π/4Т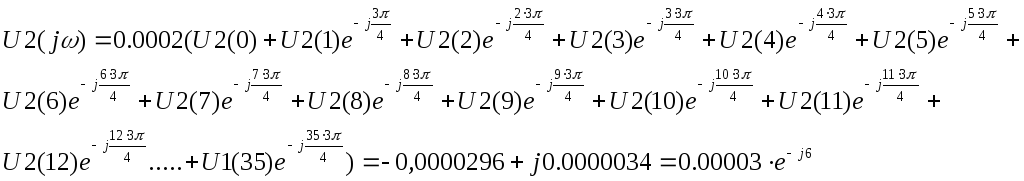
U2(jω)|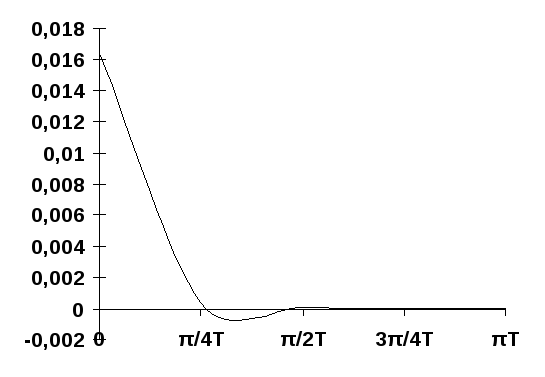
Синтез схемы дискретной цепи.
Z – преобразование импульсной характеристики цепи записывается в виде:
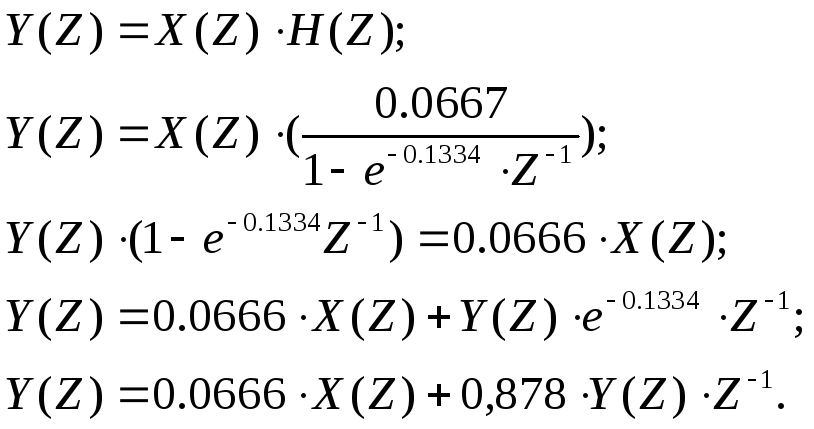
Схема дискретной цепи:
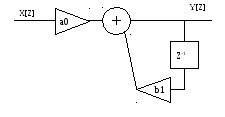
a0 = 0.0667; b1 = 0,878
Канонический вид схемы дискретной цепи:
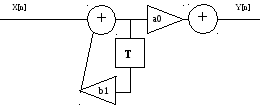
a0 = 0.0667; b1 = 0.878
Передаточная функция корректирующей цепи.
Компенсация искажений сигнала, вносимых заданной цепью может быть выполнена с помощью корректора, подключаемого ко входу или выходу цепи. При этом передаточная функция всей схемы должна быть постоянной величиной, не зависящей от частоты.
Z – преобразование передаточной функции корректора H'(Z) находится как величина, обратная H(Z) исходной цепи:
Отсчеты импульсной характеристики корректора находится путем деления полинома числителя H'(Z) на его знаменатель и перехода от Z – преобразования к функции дискретного времени H'(n).
1
-0,878·Z-1
0,0667
1
14,75
-0,878·Z-1 0,0667
-0,878·Z-1
-12,95·Z-1
0
Дискретные значения сигнала на выходе корректора вычисляются с помощью формулы дискретной свертки.
Дискретные значения сигнала на выходе корректора U’2(2)-U’2(25) я рассчитал с помощью программы написанной мною на языке turbo Pascal (см. приложение)
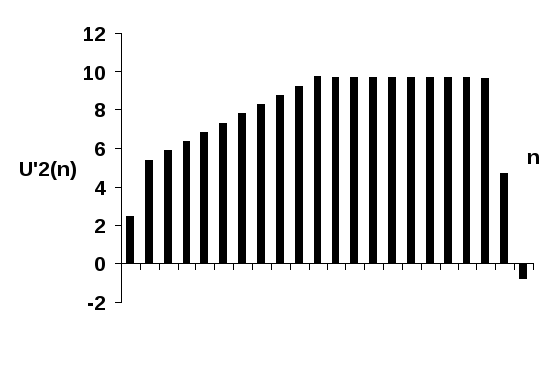
Дискретные значения импульсной характеристики корректора и его сигнала на выходе:
|
t |
0 |
0.2 |
0.4 |
0.6 |
0.8 |
1 |
1.2 |
1.4 |
1.6 |
1.8 |
2 |
|
n |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
H’(n) |
14.75 |
-12.95 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
U’2(n) |
2.46 |
5.403 |
5.88 |
6.36 |
6.84 |
7.315 |
7.79 |
8.27 |
8.75 |
9.23 |
9.71 |
|
t |
2.2 |
2.4 |
2.6 |
2.8 |
3 |
3.2 |
3.4 |
3.6 |
3.8 |
4 |
4.2 |
|
n |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
|
H’(n) |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
U’2(n) |
9.7 |
9.69 |
9.68 |
9.67 |
9.66 |
9.658 |
9.652 |
9.65 |
9.64 |
4.722 |
-0.18 |
Канонический вид схемы корректора:
a0 = 14,75; a1 = -12,95;
Аналитическое выражение передаточной функции корректирующей цепи H'(jω):
Аплитудно-частотная характеристика корректора H'(ω):
ω = 0
ω = π/2
ω = π
ω = 3π/2
ω = 2π
Аплитудно-частотная характеристика дискретной цепи H(ω):
ω = 0
ω = π/2
ω = π
ω = 3π/2
ω = 2π
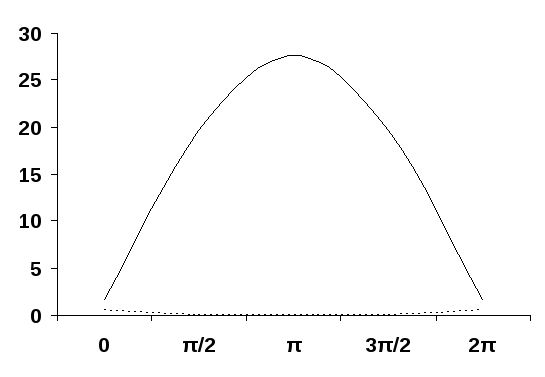
H(ω),H'(ω)
H(ω)
H'(ω)