
Курсовая ОТЦ ТЭЦ Мишина АЭС А-42 2006
.docМинистерство РФ по связи и информатизации
Сибирский Государственный Университет Телекоммуникаций и Информатики
Кафедра ТЭЦ
Курсовая работа
по курсу «Основы теории электрических цепей»
Тема: Расчет электрических цепей при импульсном воздействии
Выполнила:
Студентка группы А-42
Мишина А.В.
Проверил:
Чирков В.Д.
г. Новосибирск
2006 г.
Содержание.
-
Введение………………………………………………………………………3 стр.
-
Расчеты:
п.2.1……………………………………………………………………………...5 стр.
п.2.2……………………………………………………………………………...9 стр.
п.2.3………………………………………………………………………….....13 стр.
п.2.4………………………………………………………………………….....13 стр.
п.2.5………………………………………………………………………..…...18 стр.
п.2.6…………………………………………………………………………….19 стр.
п.2.7…………………………………………………………………………….21 стр.
-
Заключение…………………………………………………………………..24 стр.
-
Литература…………………………………………………………………....25 стр.
Введение.
Цель курсовой работы состоит в систематизации и закреплении знаний, полученных при изучении классического, операторного и спектрального методов расчета процессов в линейных электрических цепях, а также теоретических основ анализа дискретных сигналов и линейных дискретных системах.
Задание на курсовую работу содержит схему анализируемой цепи рис. 1 и входной сигнал в виде одиночного импульса, параметры которого указаны на рисунке рис. 2.

Рисунок 1 – Анализируемая схема

Рисунок 2 – Входной сигнал
Все резисторы схемы имеют сопротивление R=1 кОм, индуктивность L=1 Гн.
В процесс выполнения работы необходимо получить следующие результаты:
п.2.1 – рассчитать и построить график напряжения на выходе цепи, для этого необходимо получить аналитические выражения, описывающие U2(t) на различных интервалах времени с помощью интеграла Дюамеля, воспользоваться программой «Определение реакции цепи на импульс заданной формы с помощью интеграла Дюамеля» (DML) и вычислить значения напряжения на выходе для 12 моментов времени и построить график, затем проверить полученные выражения на нескольких интервалах времени.
п.2.2 – вычислить передаточную функцию цепи H(jω), спектральную плотность сигнала на входе и выходе цепи, построить соответствующие графики, для этого записать амплитудно- и фазо-частотные характеристики передаточной функции цепи H(ω) и Ф(ω), получить аналитические выражения спектральной плотности входного сигнала, выделив амплитудную и фазовую характеристики ее U1(ω), и Ф1(ω), рассчитать значения АЧХ и ФЧХ цепи, модуля и аргумента спектральной плотности сигнала на входе и выходе цепи с помощью программы «Спектральный метод расчета АЧХ и ФЧХ (FREAN)
п.2.3 – используя импульсную характеристику цепи, получить выражение для передаточной функции, для этого записать выражение для импульсной характеристики цепи, полученную как производную от переходной характеристики, подставить в формулу прямого одностороннего преобразования Фурье и после вычисления интеграла, записать в виде H(jω).
п.2.4 – провести дискретизацию входного сигнала и импульсной характеристики цепи, вычислить отсчеты дискретного сигнала на выходе и построить графики спектра дискретизированного сигнала и АЧХ дискретизированной цепи, для этого среди вычисленных в п.2.2 значений U1(ω) выбрать максимальное и найти частоту, выше которой модуль спектральной плотности не превышает значения 0,1U1max(ω), считая эту частоту верхней границей спектра, выбрать период дискретизации и определить значения функции входного сигнала в выбранных точках отсчета U1(n), для тех же моментов времени вычислить дискретные значения импульсной характеристики цепи h(n), воспользовавшись формулой дискретной свертки или перемножив Z – преобразования функции дискретного входного сигнала U1(z) и дискретной импульсной характеристики H(z), вычислить значения дискретной последовательности сигнала на выходе цепи U2(n) на интервале времени 0≤t<10T, сравнив результат со значениями U2(t), полученными в п.2.1.
п.2.5 – по отсчетам входного сигнала вычислить его спектральную плотность, для этого воспользовавшись аналогией между Z – преобразованием Фурье, вычислить значения спектральной плотности дискретного сигнала U1(n) на 4-5 частотах, построить график спектральной плотности дискретизированного сигнала.
п.2.6 – составить схему дискретной цепи, выполнив Z –преобразование дискретизированной импульсной характеристики, для этого рассматривая Z –преобразование дискретной импульсной характеристики цепи как системную функцию, составить схему, рассчитать и построить график АЧХ дискретной цепи.
п.2.7 – определить передаточную функцию цепи, корректирующей искажения дискретного сигнала, вносимые сконструированной дискретной цепью, рассчитать дискретный сигнал на выходе корректора, для этого передаточная функция корректирующей цепи должна быть обратна передаточной функции цепи, полученной в п.2.4, вычислив отсчеты импульсной характеристики корректирующей цепи H’(n) и применив операцию дискретной свертки к последовательностям U2(n) и Н’(n) получить результат, совпадающий со значениями U1(n), составить схему и построить графики АЧХ и ФЧХ корректирующей цепи.
2.1
На вход цепи, изображенной на рис. 1 подается импульсный сигнал U1(t), приведенный на рис. 2. Вычисляется переходная характеристика цепи, как реакция на входное воздействие в виде единичной функции 1(t). Численно она равна напряжению на выходе цепи
g(t) = U2(t)
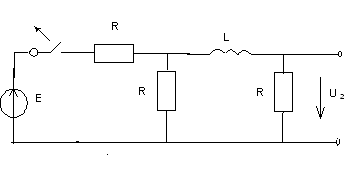
![]()
Рисунок 3
В момент коммутации при t→0
![]()
![]() т.к. ток через индуктивность скачком
не меняется
т.к. ток через индуктивность скачком
не меняется

Рисунок 4
В принужденном режиме при t→∞

Рисунок 5
![]()

ток через индуктивность будет равен
![]()
![]()
тогда
![]()
![]() Переходная
характеристика цепи
Переходная
характеристика цепи
![]()
![]()
![]()
Запишем операторное сопротивление и приравняем 0

Весь отрезок времени 0≤t<∞ разбивается на три интервала. Границы интервалов приходятся на моменты времени t0 = 0, t1 = 2 мс, t2 = 4 мс
Значения функции входного сигнала U1(t) и его производной на каждом из интервалов
1) интервал 0≤t<t1:
U1(0) = 5,
U1(t) = 5+2500t, В
U’1(t) = 2500, В/С.
2) интервал t1≤t<t2:
В момент t = t1 входной сигнал изменяется скачком от 10 до 5, следовательно, U1(t) = -5 В, а в пределах самого интервала U1(t) = 5 В; U’1(t) = 0, В/С.
3) интервал t2≤t
В момент времени t = t2 входной сигнал изменяется скачком от 5 до 0, следовательно,
U1(t) = -5 В, и в пределах самого интервала сигнал отсутствует U1(t) = 0, U’1(t) = 0.
Реакция пассивной цепи на заданное воздействие определяется при помощи интеграла Дюамеля
Интеграл Дюамеля
1)0<t<2
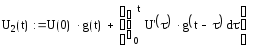

2) интервал 2≤t<4:
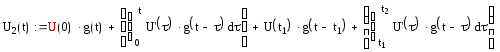

3) интервал 4≤t:

![]()
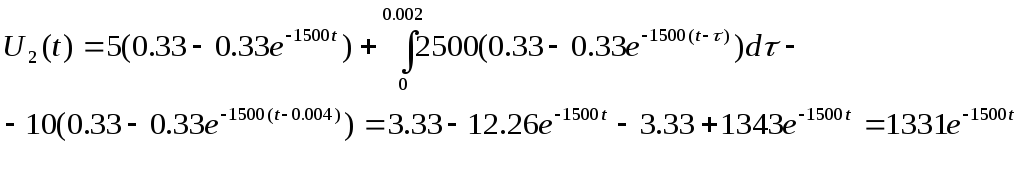
С помощью программы DML вычисляются значения U2(t) для 12 моментов времени.
Результаты расчета приведены в табл. 1 и по ним построен график U2(t) на рис. 6
Таблица 1 – Значения U2(t), вычисленные с помощью интеграла Дюамеля
|
t, мс |
0 |
0,333 |
0,666 |
1 |
1,333 |
1,666 |
2 |
2,333 |
2,666 |
3 |
3,333 |
3,666 |
|
|
U, В |
0 |
0,708 |
1,238 |
1,662 |
2,02 |
2,339 |
2,637 |
2,909 |
3,075 |
3,175 |
3,236 |
3,273 |
|
|
t, мс |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|||||
|
U, В |
3,295 |
0,735 |
0,164 |
0,037 |
0,008 |
0,002 |
0 |
|
|||||
Р исунок
6 – График зависимости выходного сигнала
от времени
исунок
6 – График зависимости выходного сигнала
от времени
Для проверки правильности нахождения интеграла Дюамеля подставляем t в формулы полученные выше и сверяем с результатами, полученными компьютерным путем:
![]() (на
первом отрезке)
(на
первом отрезке)
![]() (на первом отрезке)
(на первом отрезке)
![]() (на втором отрезке)
(на втором отрезке)
![]() ( на втором отрезке)
( на втором отрезке)
![]() ( на третьем отрезке)
( на третьем отрезке)
Результаты практически сходятся. Это позволяет сделать вывод о правильности расчетов
2.2
Для нахождения спектральной плотности входного сигнала функция U1(t) представляется в виде суммы «четырех» простейших функций:
![]() (t>0мс)
(t>0мс)
![]()
![]() (t<0мс) изображение
(t<0мс) изображение
![]()

![]() t>0
t>0
![]() t<0 изображение
t<0 изображение
![]()

![]() мс
t>2
мс
t>2
![]() мс t<2
изображение
мс t<2
изображение
![]()

![]() мс t>4
мс t>4
![]() мс t<4
изображение
мс t<4
изображение
![]()
Изображение входного сигнала записывается как сумма изображений «простейших» функции.
![]()
Заменяя в последнем выражении p на jω, получаем спектральную плотность входного сигнала
![]()
для простоты записи и вычисления разобьем это выражение на две части А и В
А:

В:

Объединим две части, т.е. сложим между собой действительную и мнимую части

Обозначим действительную часть как A, а мнимую как В. Тогда получим амплитудная характеристика спектральной плотности входного сигнала
![]()
Фазовая характеристика его
![]()
Передаточная функция по напряжению цепи, изображенной на рис. 1

 где
где
![]() ток в ветви с индуктивностью,
ток в ветви с индуктивностью,
![]() -общий
ток
-общий
ток

![]()
Амплитудно-частотная характеристика (АЧХ) этой цепи
![]()
Фазо-частотная характеристика ФЧХ
![]()
Амплитудная характеристика спектральной плотности сигнала на выходе цепи записывается в виде
![]()
Вычисление моделей и аргументов спектральных плотностей на входе и выходе цепи, а также АЧХ и ФЧХ ее производится с помощью программы «FREAN».
Результаты расчетов приведены в таблице 2, а графики функций, построенные по этим данным – на рисунках
|
F,кГц |
0 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1 |
1,1 |
|
U1(w),В |
35 |
27,32 |
10,73 |
3,811 |
5,498 |
1,593 |
3,91 |
2,461 |
1,734 |
2,498 |
0,747 |
2,104 |
|
Ф1(w), |
0 |
79,45 |
166,7 |
8,78 |
118,2 |
269,3 |
68,14 |
167,6 |
10,07 |
115,6 |
268,5 |
66,71 |
|
H(w),В |
0,333 |
0,307 |
0,256 |
0,208 |
0,171 |
0,144 |
0,123 |
0,108 |
0,095 |
0,086 |
0,077 |
0,071 |
|
Фн(w), |
0 |
-22,7 |
-40 |
-51,5 |
-59,2 |
-64,5 |
-68,3 |
-71,2 |
-73,4 |
-75,2 |
-76,6 |
-77,8 |
|
U(w),В |
11,67 |
8,401 |
2,743 |
0,791 |
0,94 |
0,229 |
0,482 |
0,265 |
0,165 |
0,214 |
0,062 |
0,143 |
|
Ф2(w), |
0 |
56,72 |
126,7 |
-42,7 |
59,03 |
204,8 |
0,188 |
96,36 |
-63,3 |
40,41 |
191,9 |
-11,1 |
|
F,кГц |
1,2 |
1,3 |
1,4 |
1,5 |
1,6 |
1,7 |
1,8 |
1,9 |
|
U1(w),В |
1,38 |
1,107 |
1,617 |
0,531 |
1,438 |
0,96 |
0,811 |
1,196 |
|
Ф1(w), |
167,5 |
10,04 |
114,7 |
267,8 |
66,01 |
167,3 |
9,829 |
114,1 |
|
H(w),В |
0,065 |
0,06 |
0,056 |
0,052 |
0,049 |
0,046 |
0,044 |
0,042 |
|
Фн(w), |
-78,8 |
-79,6 |
-80,4 |
-81 |
-81,6 |
-82 |
-82,5 |
-82,9 |
|
U(w),В |
0,09 |
0,067 |
0,091 |
0,028 |
0,071 |
0,045 |
0,036 |
0,05 |
|
Ф2(w), |
88,7 |
-69,6 |
34,31 |
186,8 |
-15,5 |
85,23 |
-72,7 |
31,23 |


Рисунок 7 - Амплитудные и фазовые характеристики спектров сигналов на входе и выходе цепи и ее частотные свойства
2.3
Временные и частотные характеристики цепи связаны между собой формулами преобразования Фурье. По найденной в п. 2.1 переходной характеристике вычисляется импульсная характеристика цепи (рисунок 1)
![]()
![]()
![]()
Результат вычислений совпадает с формулой H(jω), полученной в п. 2.2
2.4
Пусть принимается за верхнюю границу
спектра входного сигнала
![]() .Тогда
по теореме Котельникова частота
дискретизации
.Тогда
по теореме Котельникова частота
дискретизации
![]() кГц.
Откуда период дискретизации T=0.1мс
кГц.
Откуда период дискретизации T=0.1мс
По графику, изображенному на рис.1, определяем значения дискретных отсчетов входного сигнала U1(n) для t моментов дискретизации.
Дискретные значения импульсной характеристики вычисляются по формуле
![]() где T=0.0001 с; n=0,
1, 2,…., 20
где T=0.0001 с; n=0,
1, 2,…., 20
Таблица 3 – Дискретные значения функции входного сигнала и импульсной характеристики
|
t, c |
n |
U1(n) |
H(n) |
|
0 |
0 |
5 |
0,05000 |
|
0,0001 |
1 |
5,25 |
0,04304 |
|
0,0002 |
2 |
5,5 |
0,03704 |
|
0,0003 |
3 |
5,75 |
0,03188 |
|
0,0004 |
4 |
6 |
0,02744 |
|
0,0005 |
5 |
6,25 |
0,02362 |
|
0,0006 |
6 |
6,5 |
0,02033 |
|
0,0007 |
7 |
6,75 |
0,01750 |
|
0,0008 |
8 |
7 |
0,01506 |
|
0,0009 |
9 |
7,25 |
0,01296 |
|
0,001 |
10 |
7,5 |
0,01116 |
|
0,0011 |
11 |
7,75 |
0,00960 |
|
0,0012 |
12 |
8 |
0,00826 |
|
0,0013 |
13 |
8,25 |
0,00711 |
|
0,0014 |
14 |
8,5 |
0,00612 |
|
0,0015 |
15 |
8,75 |
0,00527 |
|
0,0016 |
16 |
9 |
0,00454 |
|
0,0017 |
17 |
9,25 |
0,00390 |
|
0,0018 |
18 |
9,5 |
0,00336 |
|
0,0019 |
19 |
9,75 |
0,00289 |
|
0,002 |
20 |
10 |
0,00249 |
|
0,0021 |
21 |
10 |
0,00214 |
|
0,0022 |
22 |
10 |
0,00184 |
|
0,0023 |
23 |
10 |
0,00159 |
|
0,0024 |
24 |
10 |
0,00137 |
|
0,0025 |
25 |
10 |
0,00118 |
|
0,0026 |
26 |
10 |
0,00101 |
|
0,0027 |
27 |
10 |
0,00087 |
|
0,0028 |
28 |
10 |
0,00075 |
|
0,0029 |
29 |
10 |
0,00065 |
|
0,003 |
30 |
10 |
0,00056 |
|
0,0031 |
31 |
10 |
0,00048 |
|
0,0032 |
32 |
10 |
0,00041 |
|
0,0033 |
33 |
10 |
0,00035 |
|
0,0034 |
34 |
10 |
0,00030 |
|
0,0035 |
35 |
10 |
0,00026 |
|
0,0036 |
36 |
10 |
0,00023 |
|
0,0037 |
37 |
10 |
0,00019 |
|
0,0038 |
38 |
10 |
0,00017 |
|
0,0039 |
39 |
10 |
0,00014 |
|
0,004 |
40 |
10 |
0,00012 |
