
- •5. Метод экспертных оценок
- •Этап 1 Организационный этап
- •Этап 2 Выбор метода опроса
- •Этап 3 Выбор метода измерения информации, получаемой от экспертов
- •Этап 4 Обработка полученных данных и оценка согласованности мнений экспертов
- •4.1 На основе данных предыдущего этапа составляется матрица рангов
- •4.2 Расчет стандартизированных рангов
- •Составляется матрица стандартизированных рангов. Для упрощения расчетов в предыдущей таблице в скобках можно указать номер позиции каждого из объектов.
- •1 2 2 2 3 3 4 4 4 5 6
4.2 Расчет стандартизированных рангов
Стандартизированные ранги рассчитываются как средняя арифметическая суммы мест позиций объектов с одинаковыми рангами.
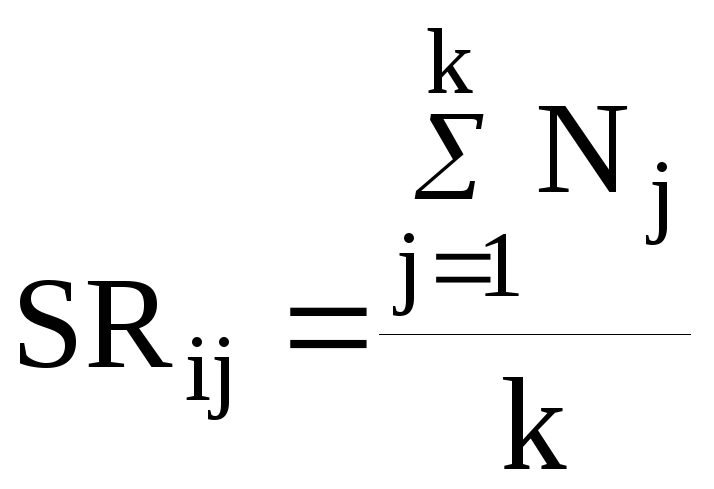 ,
,
где
![]() -
стандартизированный ранг,
-
стандартизированный ранг,
![]() -
сумма позиций объектов с одинаковыми
рангами,
-
сумма позиций объектов с одинаковыми
рангами,
k – число объектов с одинаковыми рангами.
Составляется матрица стандартизированных рангов. Для упрощения расчетов в предыдущей таблице в скобках можно указать номер позиции каждого из объектов.
|
Факторы риска |
Эксперты | ||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 | |
|
F1 |
3 (4) |
4 |
3 (3) |
2 (3) |
3 |
3 (5) |
2 (3) |
|
F2 |
2 (2) |
3 |
2 (2) |
2 (2) |
2 |
1 (1) |
1 (1) |
|
F3 |
1 (1) |
1 |
1 (1) |
1 (1) |
1 |
1 (2) |
1 (2) |
|
F4 |
2 (3) |
2 |
4 (5) |
4 (4) |
4 |
2 (3) |
3 (4) |
|
F5 |
4 (5) |
5 |
3 (4) |
5 (5) |
5 |
2 (4) |
4 (5) |
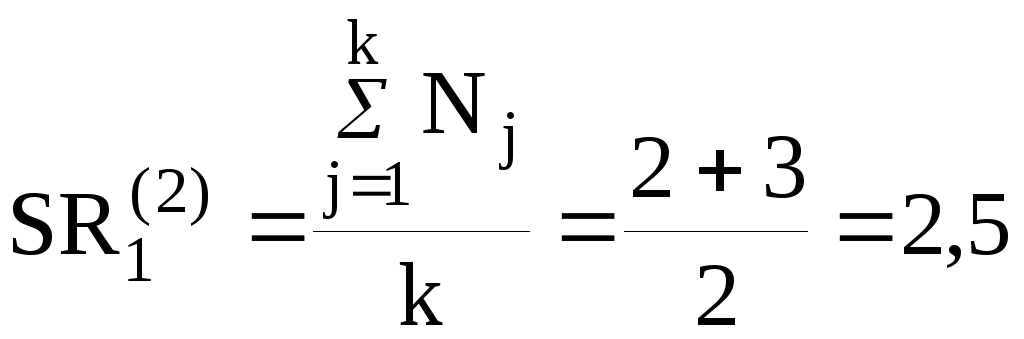
Таблица 2 – Матрица стандартизированных рангов
|
Факторы риска |
Эксперты (n) |
|
di |
| ||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 | ||||
|
F1 |
4 |
4 |
3,5 |
2,5 |
3 |
5 |
3 |
25 |
4 |
16 |
|
F2 |
2,5 |
3 |
2 |
2,5 |
2 |
1,5 |
1,5 |
15 |
-6 |
36 |
|
F3 |
1 |
1 |
1 |
1 |
1 |
1,5 |
1,5 |
8 |
13 |
169 |
|
F4 |
2,5 |
2 |
5 |
4 |
4 |
3,5 |
4 |
25 |
4 |
16 |
|
F5 |
5 |
5 |
3,5 |
5 |
5 |
3,5 |
5 |
32 |
11 |
121 |
|
Итого |
15 |
15 |
15 |
15 |
15 |
15 |
15 |
105 |
- |
358 |
|
|
|
|
|
|
|
|
|
|
|
|
В оценках 2-ого эксперта нет повторяющихся, поэтому значения 2-го столбца будут совпадать со значениями предыдущей таблицы.
Оценки 3-го эксперта:
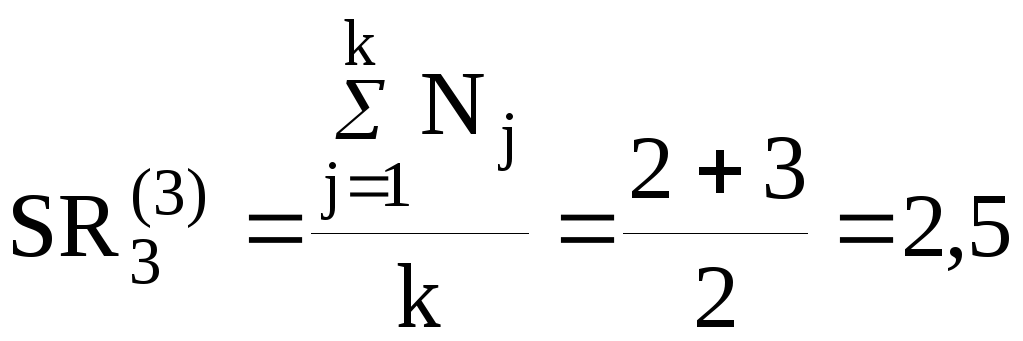
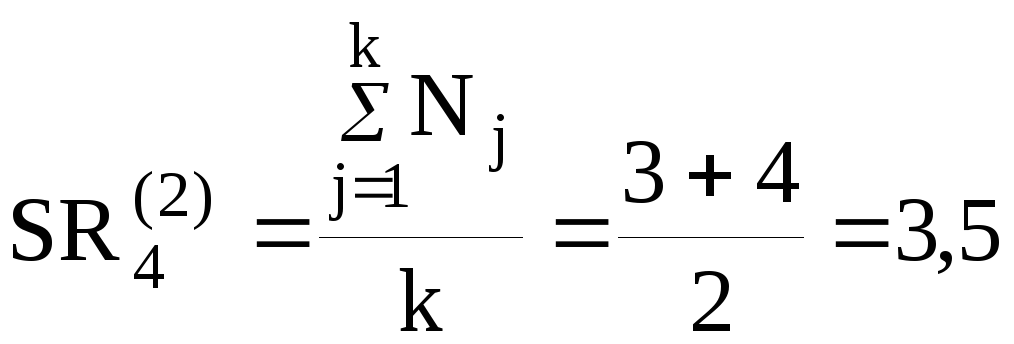
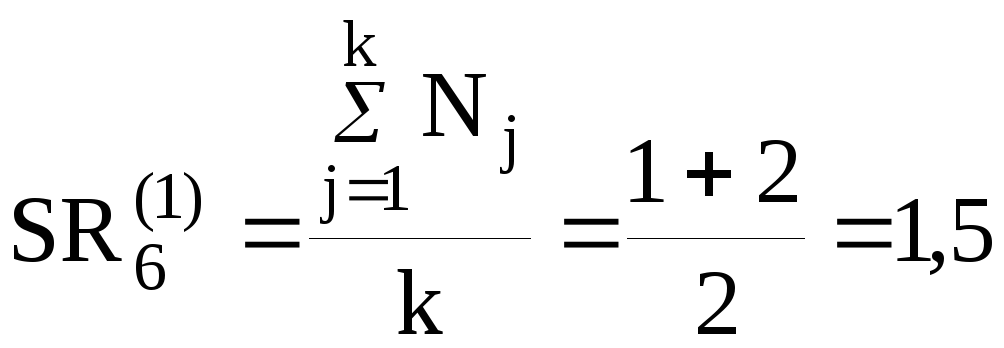
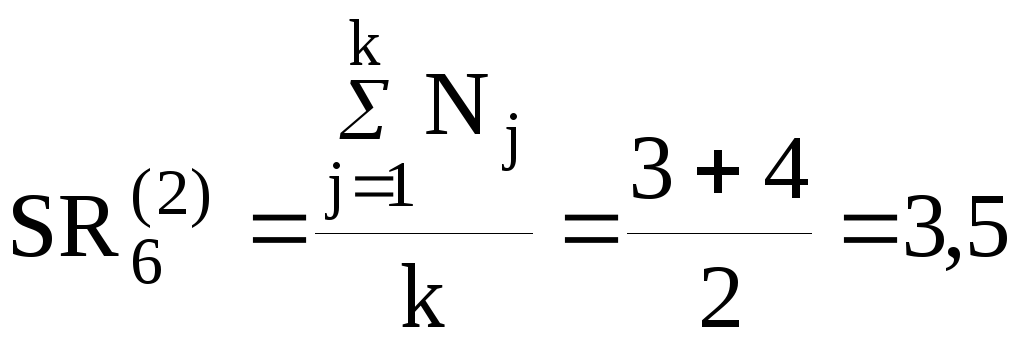
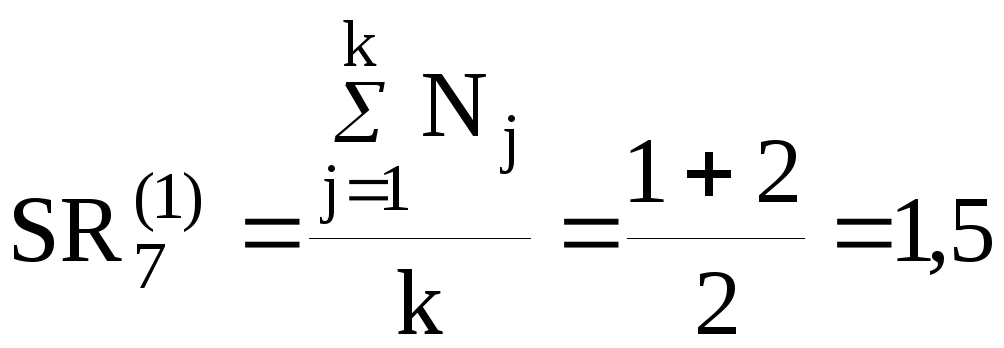
Оценка согласованности мнений экспертов
Для оценки согласованности мнений экспертов необходимо рассчитать коэффициент конкордации.
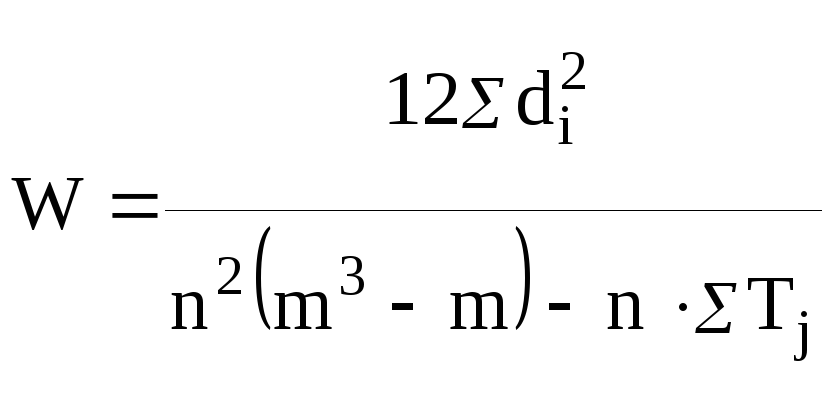 ,
,
где n – количество экспертов,
m – количество объектов,
di – отклонение суммы стандартизированных рангов от среднего значения,
Tj – показатель связанных рангов.
Расчет![]() :
:
Для
расчета ![]() необходимо
определить среднее
значение суммы стандартизированных
рангов:
необходимо
определить среднее
значение суммы стандартизированных
рангов:
![]() ,
,
![]()
В данном примере:
![]() ,
,
тогда:
![]() =
25 – 21 = 4
=
25 – 21 = 4
![]() =
15 – 21 = - 6
=
15 – 21 = - 6
![]() =
8 – 21 = -13
=
8 – 21 = -13
![]() =25–
21 = 4
=25–
21 = 4
![]() =
32 – 21 = 11
=
32 – 21 = 11
Далее для расчета коэффициента конкордации необходимо определить показатель связанных рангов:
![]() ,
,
где z – число групп объектов равных рангов в оценках j-ого эксперта,
![]() -
число объектов с одинаковыми рангами.
-
число объектов с одинаковыми рангами.
Рассмотрим на примере следующей ранжировки:
1 2 2 2 3 3 4 4 4 5 6
Т.е. имеется 3 группы объектов равных рангов, причем:
1-ая группа включает три объекта,
2-ая группа включает два объекта,
3-яя группа включает три объекта.
Показатель связанных рангов будет равен:
![]() =
(33-3)
+ (23-2)+(33-3)
= 24 + 6 + 24 =54
=
(33-3)
+ (23-2)+(33-3)
= 24 + 6 + 24 =54
В рассматриваемой задаче:
|
Факторы риска |
Эксперты (n) |
|
di |
| ||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 | ||||
|
F1 |
4 |
4 |
3,5 |
2,5 |
3 |
5 |
3 |
25 |
4 |
16 |
|
F2 |
2,5 |
3 |
2 |
2,5 |
2 |
1,5 |
1,5 |
15 |
-6 |
36 |
|
F3 |
1 |
1 |
1 |
1 |
1 |
1,5 |
1,5 |
8 |
13 |
169 |
|
F4 |
2,5 |
2 |
5 |
4 |
4 |
3,5 |
4 |
25 |
4 |
16 |
|
F5 |
5 |
5 |
3,5 |
5 |
5 |
3,5 |
5 |
32 |
11 |
121 |
|
Итого |
15 |
15 |
15 |
15 |
15 |
15 |
15 |
105 |
- |
358 |
|
Tj |
6 |
0 |
6 |
6 |
0 |
12 |
6 |
|
|
|
T1 = 23-2 = 6
T2 = 0
T3 = 23-2 = 6
T4 = 23-2 = 6
T5 = 0
T6 = (23-2) + (23-2)= 12
T7 = 23-2 = 6
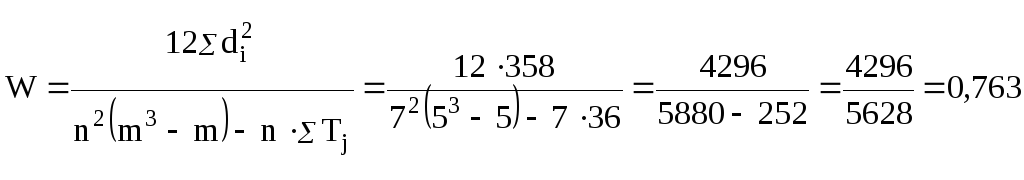
Таким образом, можно сделать вывод, что согласованность мнений экспертов достаточно высокая.
Оценка значимости коэффициента конкордации с помощью критерия согласия Пирсона
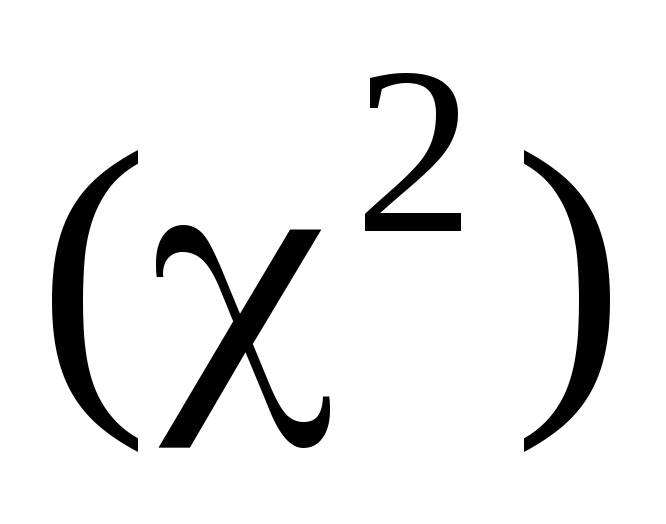
Вывод о значимости коэффициента конкордации делается в том случае, если выполняется условие:
![]() ,
,
Расчетное
значение
![]() определяется по формуле:
определяется по формуле:
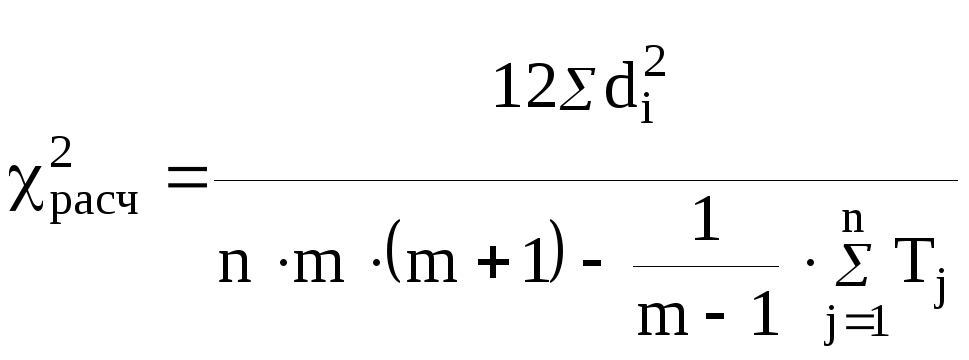 ,
,
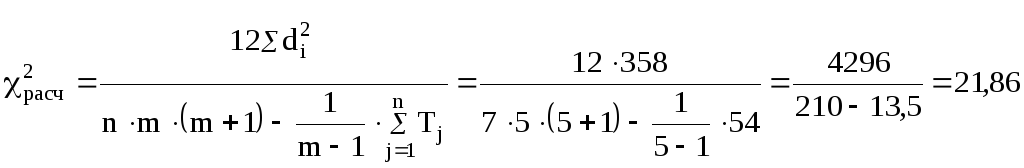
По
специальной таблице определяем значение
![]() в
зависимости от заданной вероятности и
числа степеней свободы:
в
зависимости от заданной вероятности и
числа степеней свободы:
Число степеней свободы равно количеству сравниваемых объектов минус 1.
h = m - 1
h = 5 – 1 = 4
вероятность примем равной 95%.
Тогда
по таблице находим, что
![]() =9,48
=9,48
Таким
образом, можно сделать вывод, что условие
![]() выполняется
выполняется
![]() =
21,86
=
21,86
![]() =9,48
=9,48
Это значит, что с вероятностью 95% можно утверждать, что согласованность мнений экспертов высокая.
Определим относительную значимость каждого фактора:
![]() цена
цена
![]() дизайн
дизайн
![]() интенсивность
рекламной кампании
интенсивность
рекламной кампании
![]() сервисное
обслуживание
сервисное
обслуживание
![]() качество
качество
Наиболее значимым фактором, оказывающим влияние на уровень конкурентоспособности продукции, с точки зрения членов экспертной группы, является качество продукции (F5).
Далее идут цена и сервисное обслуживание, затем – дизайн и интенсивность рекламной кампании.
