ТЭС 2011

ТЭС

1. Сообщения передаются пятиэлементным кодом с равновероятными элементами по Гауссовскому каналу связи со скоростью V=1000 Бод сигналами фазовой модуляции при отношении сигнал/шум h²=5

Рассчитать вероятность неправильного приема кодовой комбинации. Для повышения помехоустойчивости используется корректирующий код(n,k)=(9,5), исправляющий однократные ошибки t_ош=1. Рассчитать вероятность ошибочного декодирования принимаемых комбинаций при исправлении ошибок.

Решение:

Р –вероятность ошибочного приема одного элемента . q-вероятность правильного приема=1-р. Рпр=q1*q2*q3*q4*q5=q⁵. Р непр=1-(1-р)⁵.

Р определяется из формулы: рош=1/2(1-Ф(∙h))

Ф-интеграл вероятности, находим по таблице Методических указаний, приняв что х=3,15

h=√h²=√5=2,23 рош=1/2(1-Ф(∙2,23))=8,2 ∙10^-4

Р непр=1-(1-8,2∙10^-4)⁵=0,004

Исправление ошибок: (n,к)=(9.5) Для расчета необходимо пользоваться распределением кратностей ошибки (tош) .0<= tош<=n(ошибочный прием).

P_{ПР пр} + Р_{НЕПР ПР} = 1,

Р_{ПР пр} = 1-Р_непрпр = 1-0,004=0,996

Т.к. канал гаусовский , то ошибки будут незначительными и их кратность определяется биномиальным законом распределения. tош=р^tош (1-р)^n*tош

Рn(tош)=∑Сn^tош * р^tош (1-р)^n-tош

Обычно составляющие при tош >=3 пренебрежимо малы.

^{Посчитаем для двух составляющих}

P_ОШ.ДЕК = C₉² p²(1- p)^9-2 + C₉³ p³(1- p)^9-3 =36∙0,004 ∙(1-0,004)+

+ 83 0,004 ∙(1-0.004)= 0,00056+0,0000052 =0,00057 .

2. Определить амплитуды сигналов на входе идеального приемника Котельникова при дискретной фазовой модуляции (ДФМ) для следующих условий: априорные вероятности передачи сигналов равны ; спектральная плотность мощности флуктуационной помехи на входе приемника ; средняя вероятность ошибки .

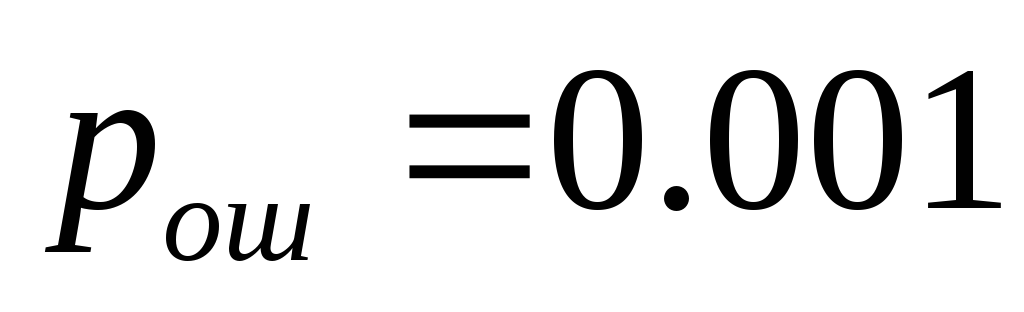Решение:

Пусть V= 1000 Бод

Так как используется ДФМ, то p_ош находим по формуле

,

где -отношение средней мощности сигнала к средней мощности помехи:

, отсюда следует, что

с другой стороны , чтобы найти , необходимо определить .

Пользуясь таблицей методических указаниях для практических работ, найдем :

√2∙h = 3,10 = = 2,19

Известно, что , , тогда

Вт, тогда

Вт.

Очевидно, что , тогда В

Ответ: =В.

3. На входе фильтра, согласованного с дискретным сигналом вида 1,-1,1,-1,1, имеющим амплитуду 1 В и общую длительность 5 мкс, действует сигнал и белый шум со спектральной плотностью . Изобразить временную диаграмму заданного сигнала и определить отношение сигнал/шум на выходе фильтра.

Решение:

Временная диаграмма заданного сигнала выглядит следующим образом:

τ_ЭЛ

U_t

1

1

1

-1

-1

t

Tс

Отношение сигнал/шум в данном случае находится по формуле:

;

Причем ;

; тогда

;

.

Ответ: =5.

4. При заданной реализации принимаемого сигнала z(t) апостериорные вероятности передаваемых сигналов «1» и «0» равны 0,7 и 0,3 соответственно. Какой символ зарегистрирует приемник, оптимальный по критерию максимального правдоподобия.

Решение: при наличии помех сигналы искажаются и для их описания используют вероятностное пространство, сами сигналы вместе с помехами описываются функциями плотности вероятности W(z/x₁) и W(z/x₂).

1. 

2. 

Проверим решение

>

0.7 > 0.3

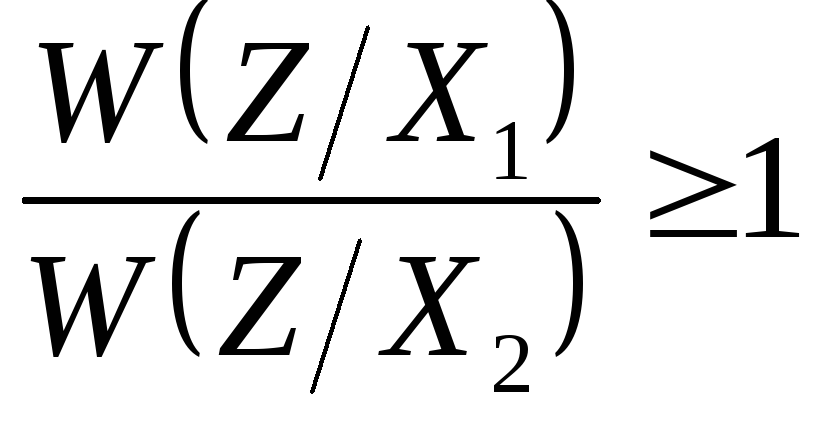
Отсюда следует что будет принят сигнал «1»

5. Непрерывный гауссовский канал связи используется для передачи двоичных равновероятных сообщений со скоростью 1000 Бод. Полоса пропускания канала связи 4 кГц, отношение сигнал/шум

. Вычислить коэффициент использования пропускной способности канала связи.

Решение:

Поскольку коэффициент использования пропускной способности канала связи находится по формуле:

, то

решение задачи сводится к нахождению пропускной способности канала по формуле Шеннона:

;

Так как канал непрерывный, то пропускная способность канала ровна:

,

причем , тогда:

.

Найдем R:

,

где =2 – основание кода;

, тогда

.

Ответ: = .

6. Определить энтропию, избыточность и производительность двоичного источника дискретных сообщений, у которого априорная вероятность передачи символа равна 0.3, а скорость передачи 9600 Бод.

Решение:

Энтропия источника сообщений – среднее количество информации, приходящееся на одно сообщение, находится по формуле:

.

Избыточность находим по следующей формуле:

Производительность источника определяется количеством информации, передаваемой в единицу времени:

Рассчитаем эти величины.

а. Поскольку в данной задаче используется двоичный код

,

то найдем исходя из того, что полная группа событий:

+=1

=1-0.3=0.7

Пользуясь таблицей на странице 63 в методических указаниях для практических работ нейдем значение энтропии:

б. Найдем избыточность.

Поскольку

,

где ,

то

в. Для того, чтобы рассчитать

производительность, найдем

Ответ:,,

7. Закодировать сообщение источника с зависимыми сообщениями и для передачи:

а. Равномерным двоичным кодом;

б. Оптимальным кодом Шеннона-Фано, объединяя по два элемента.

Вычислить производительность источника и избыточность в обоих случаях и сравнить их между собой для следующих исходных данных: ; ; вероятности переходов ;; полная энтропия источника .

Решение:

а. Равномерный код.

;

б. Оптимальный код Шеннона-Фано

Статистическое кодирование предполагает использование неравномерного кода

Для этого:

1. Все комбинации записываются в порядке убывания вероятностей

2. Начиная снизу комбинации объединяются попарно, а их вероятности складываются пока не дойдем до верху.

3. Определяем структуру комбинаций путем обхода кодового дерева от узла к сообщению.

4. Находится средняя длительность сообщения непрерывного кода, которая должна быть

1

0,49 0 0

0 10

0,21

0,51 1

110

0,21 0

0,3 1

0,09 1 111

А Равномерный код

Для равномерного кода сообщения кодируются следующими комбинациями:

00 – кодируется 1-ое сообщение; 01 – кодируется второе сообщение; 10 – кодируется 3-ье сообщение; 11 – кодируется 4-ое сообщение.

Б. Оптимальный неравномерный код

При неравномерном коде сообщения кодируются следующим образом:

Например: сообщение 1 кодируем символом «0» тогда символ «1» является запрещенным;

сообщение 2 кодируем комбинацией «01» остальные являются запрещенными;

сообщение 3 кодируем комбинацией «001»;

сообщение 4 кодируем комбинацией «0001».

Видно что равномерный код более удобен так как сообщение кодируется комбинацией символов с постоянной длинной когда как при неравномерном коде сообщения кодируется переменной длинной комбинацией символов. Для нашего случая при равномерном коде одно сообщение кодируется 2 символами а при неравномерном коде при кодировании каждого следующего сообщения количество элементов увеличивается на один.

8.Сообщение передается последовательностью амплитудно-модулированных импульсов с заданным шагом квантования . На сообщение накладываются шумы с нормальным законом распределения вероятности и дисперсией . Определить величину минимально допустимого шага квантования, при котором вероятность ошибки из-за шумов не превысит значения 0.05 (как известно, ошибка при квантовании возникает при условии, что мгновенное значение шума превышает половину шага квантования).

В соответствии с теоремой Котельникова любой непериодический сигнал U(t) можно представить отсчетами равным где Fв граничная частота исходного непрерывного сигнала шаг дискретизации (по Котельникову)

N_iразр=N_max=2^N-1

Вероятность ошибки квантования, при условии что уровень шума

Из таблицы методических указаний находим, что будет при х=1.6 равно .

Окончательно

9.На электронное реле воздействует случайное напряжение с релеевской плотностью распределения вероятностей и дисперсией =1 В². Определить вероятность срабатывания реле при условии, что порог срабатывания реле равен 2 В. Сущность задачи проиллюстрировать приведением графиков .

- это закон Релея

σ²=1в²=в U_пор=2в

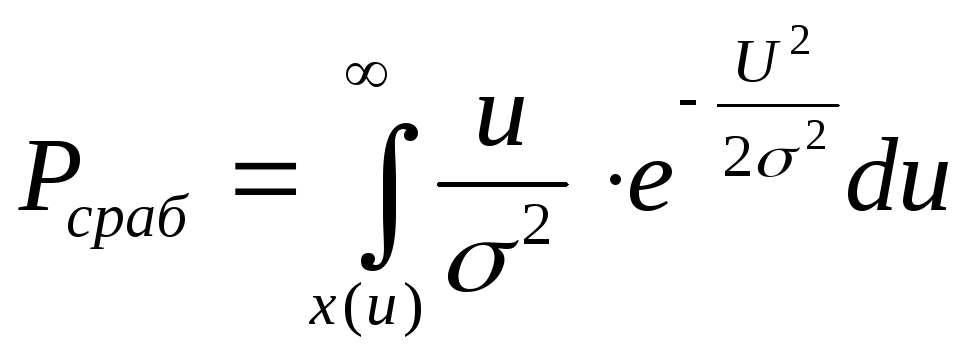
= = х = =0,135

du = dx

2

10. Вследствие замираний амплитуда радиосигнала на приеме случайна и распределена по закону Релея с дисперсией =2 В². Радиосигнал принимается на три разнесенные антенны, так что сигналы в каждой из антенн являются независимыми. Вычислить вероятность

того, что сигнал на всех антеннах одновременно уменьшится ниже уровня 1,5 В.

= = х = = 0,32

du = dx

1,5

- т.к события не зависимы вероятность того, что сигнал уменьшится ниже уровня 1,5В на одной антенне

p_1,2,3(U_c123‹1,5)=(p₁(U_c1‹1,5в))³

Вероятность того, что сигнал уменьшится на трех антеннах сразу равен:

11.Определить требуемую полосу пропускания канала передачи телевизионного изображения объемом 5 ^.10⁵ элементов при 25 кадрах в секунду и 8 равновероятных градациях яркости для соотношения сигнал/шум и при условии, что изображение может принимать вид белого шума (т.е. наиболее хаотичный вид).

Решение:

Расчет основан на теореме Шеннона для пропускной способности непрерывного канала связи

V=5∙10⁵∙25=1,25∙10⁷ бит Необходимо учесть 8 градаций яркости для этого нужен 3-х разрядный код

n=log₂8 = 3 ^бит/_{1 эл-т}

С₌V∙N=1.25∙10⁷∙3 = 3.75∙10^{7 бит}/_с

Отсюда находим полосу пропускания

Ответ: =8.5

12. Непрерывное сообщение с верхней границей спектра преобразуется методом ИКМ в двоичный сигнал с количеством уровней квантования 256. определить скорость передачи двоичных символов в канале связи.

Решение:

U(t)→ Fв = 3 кГц

В соответствии с теоремой Котельникова находим

на Δtдолжно быть «уложено» длительность τ_эл →

Скорость передачи находим по формуле:

;