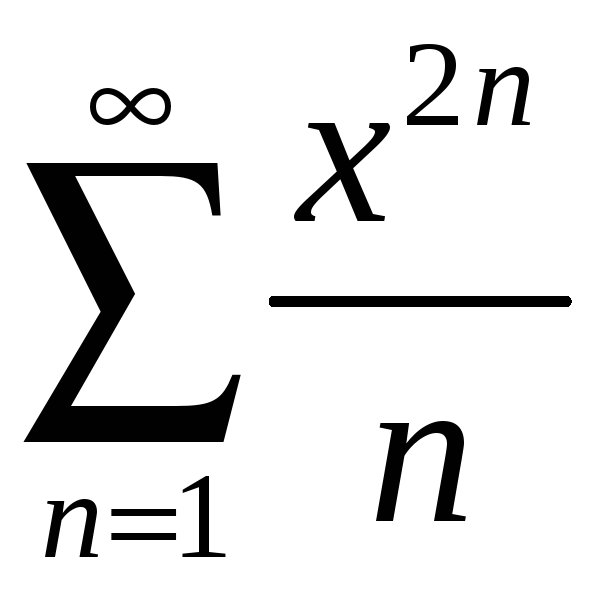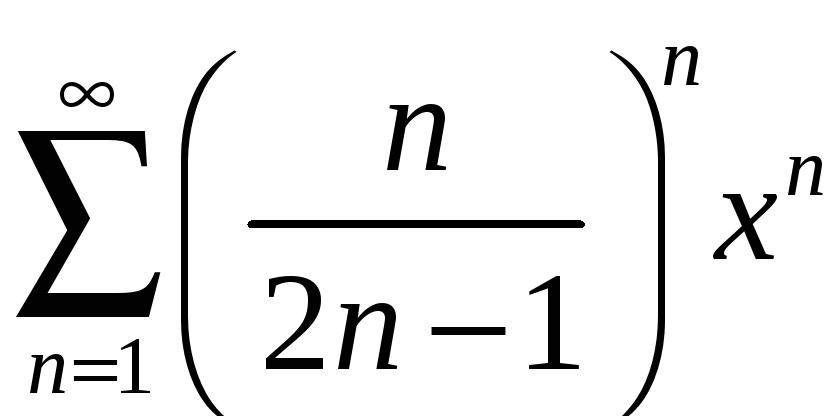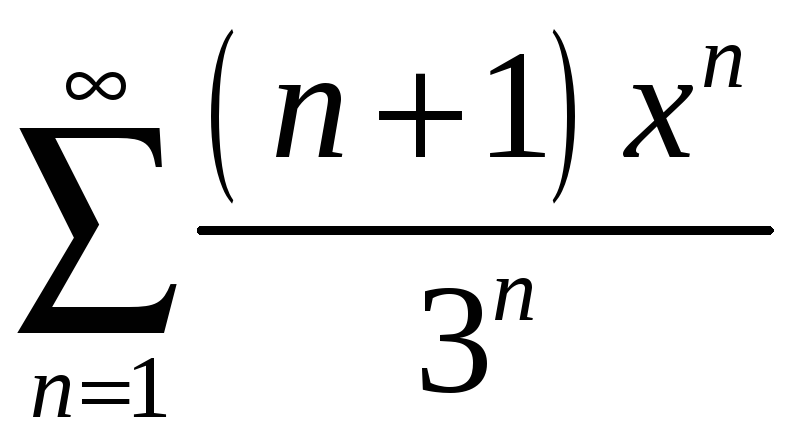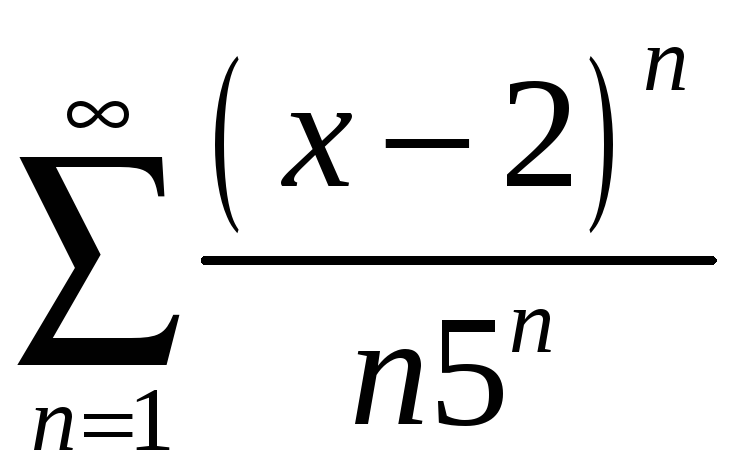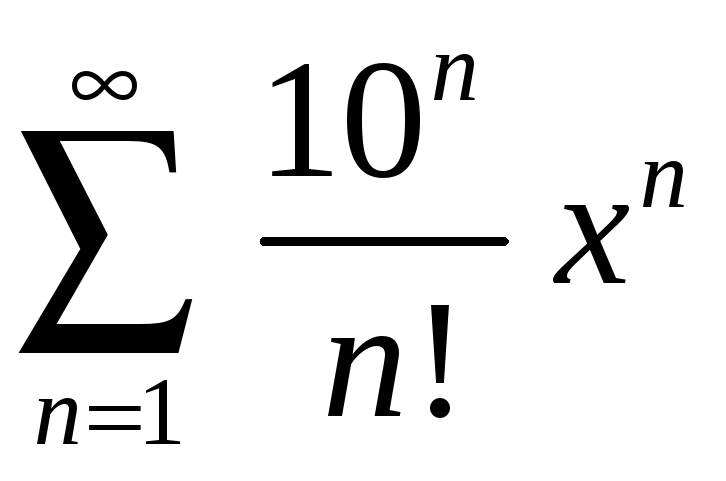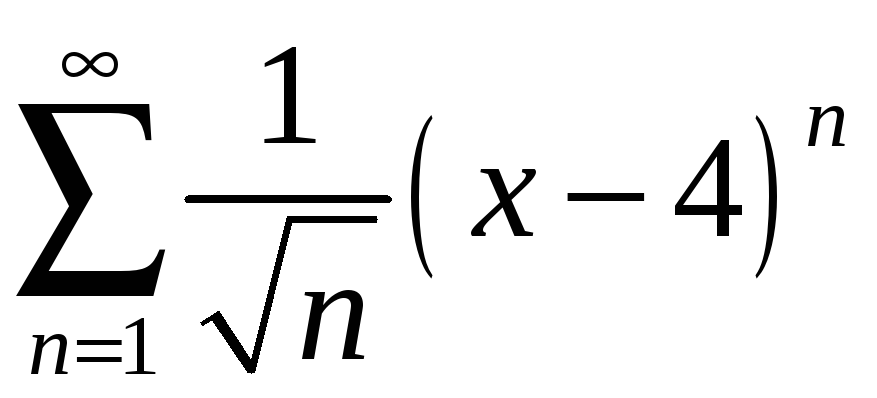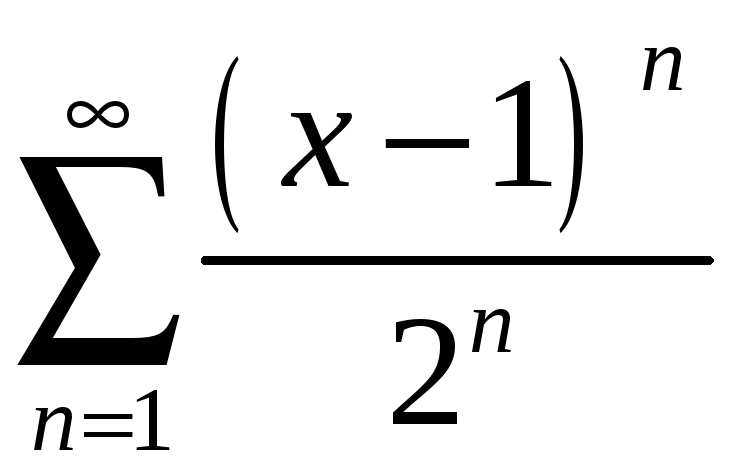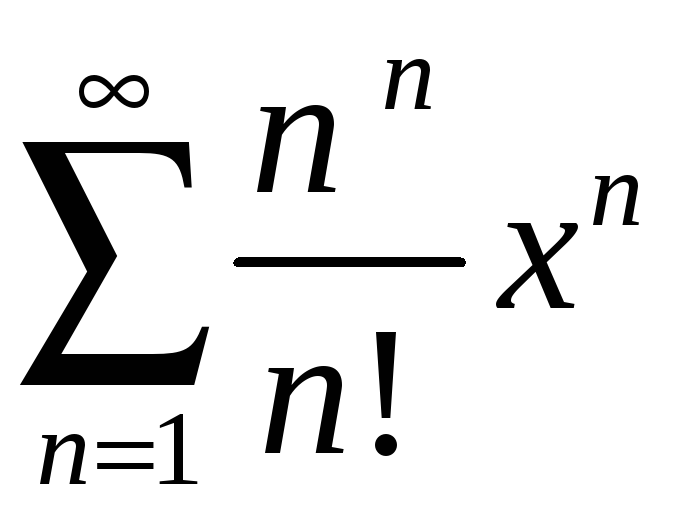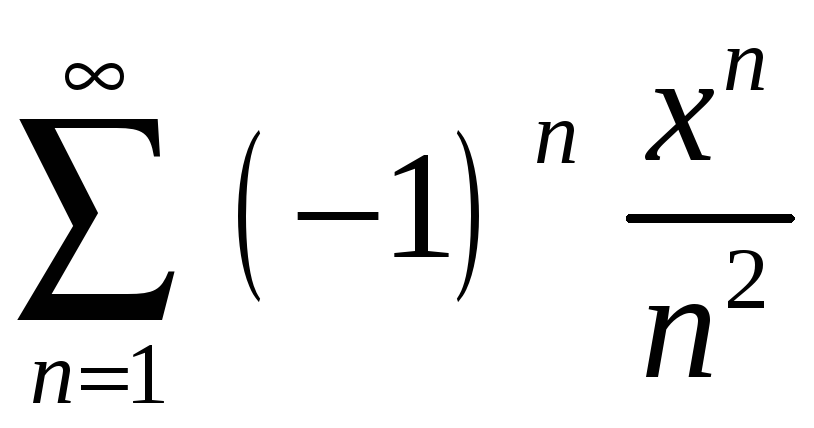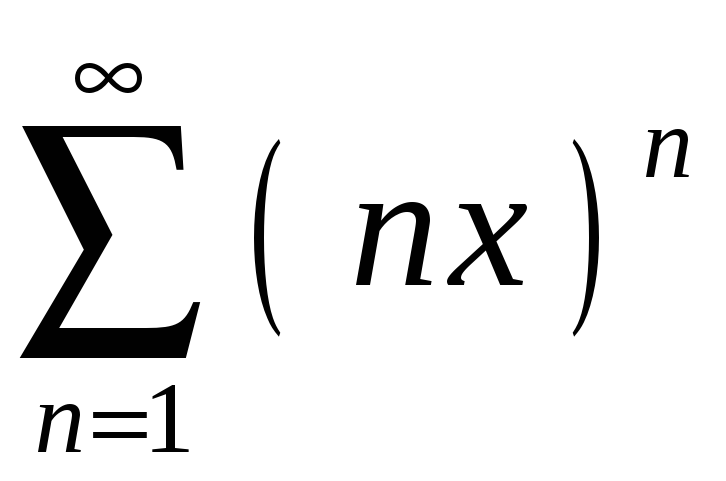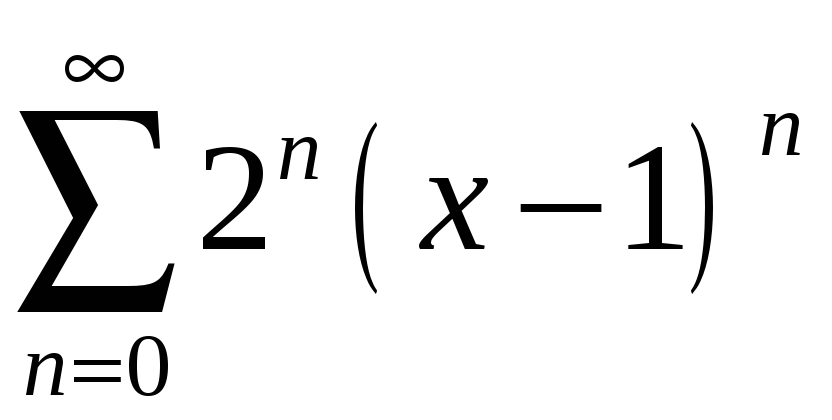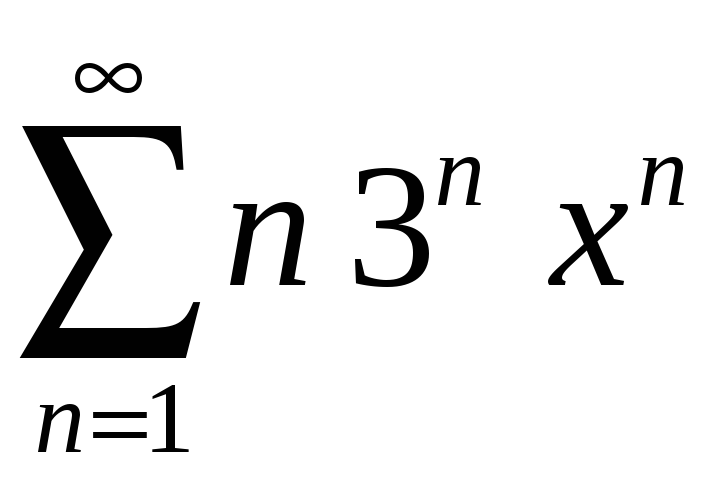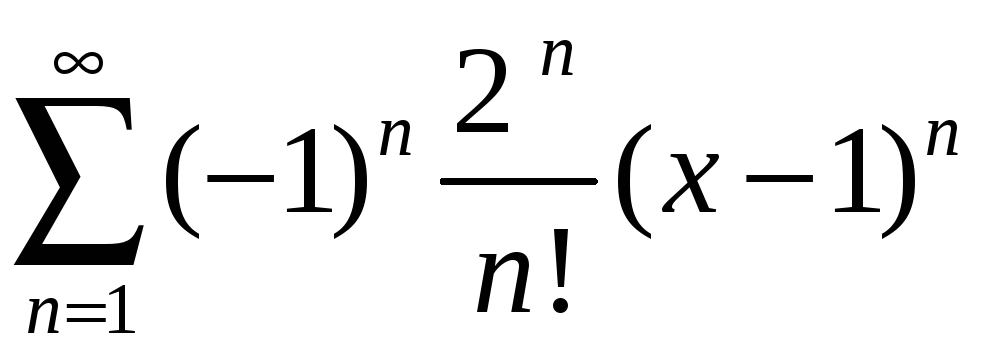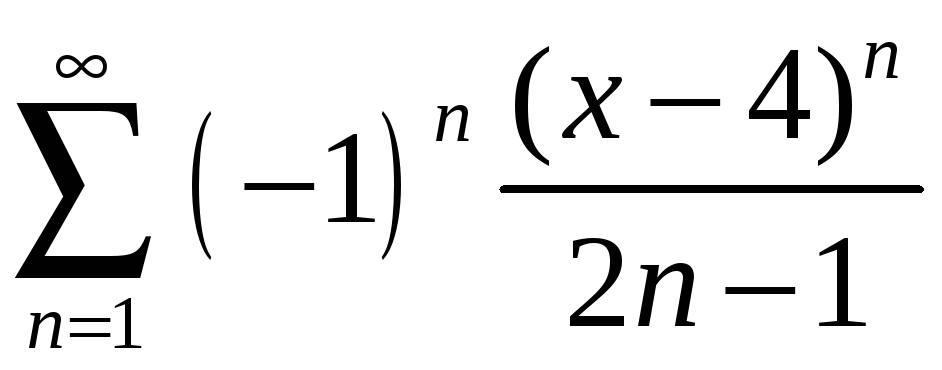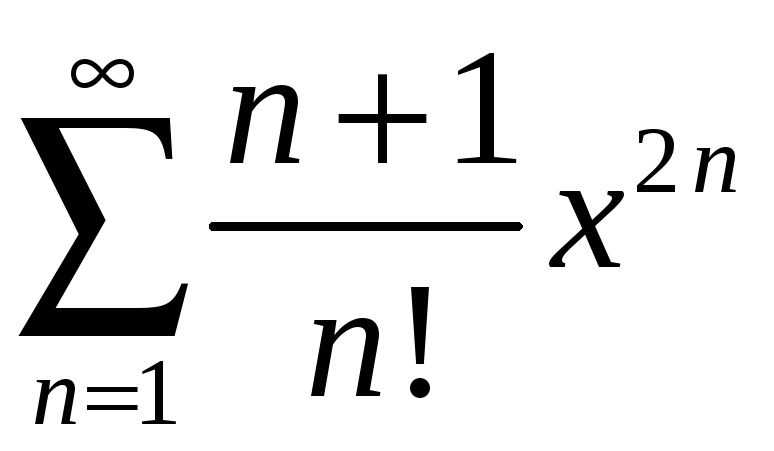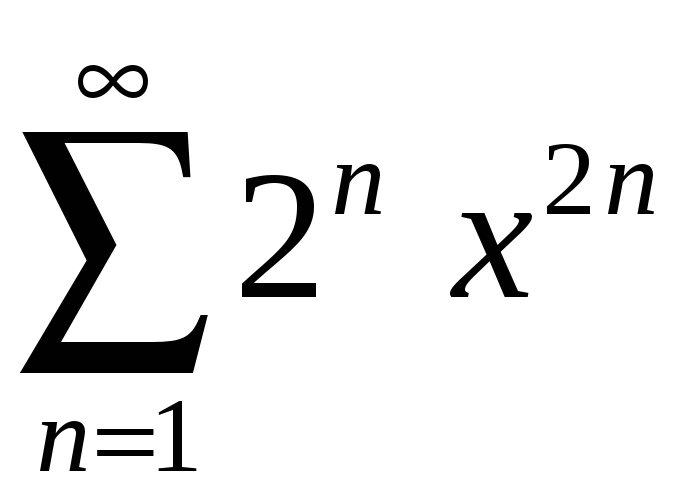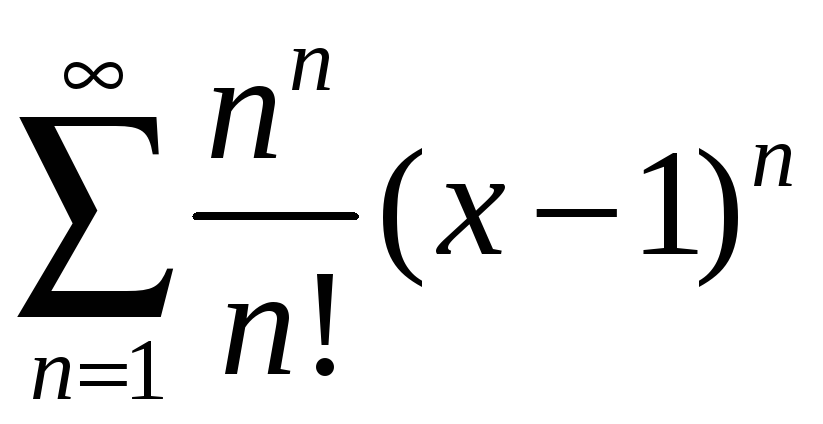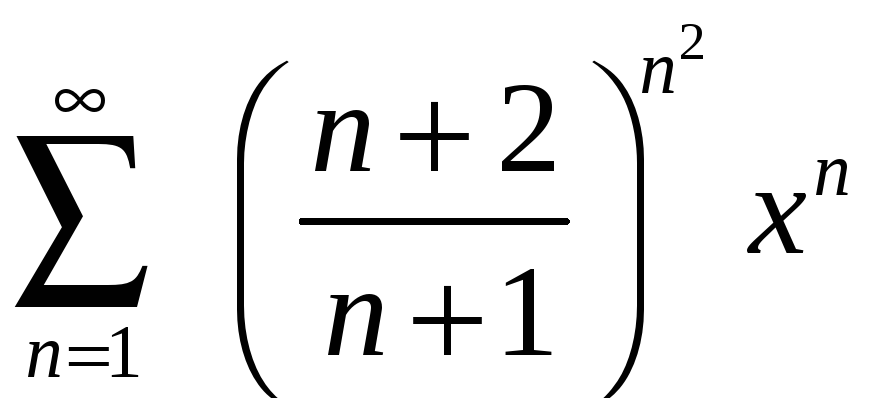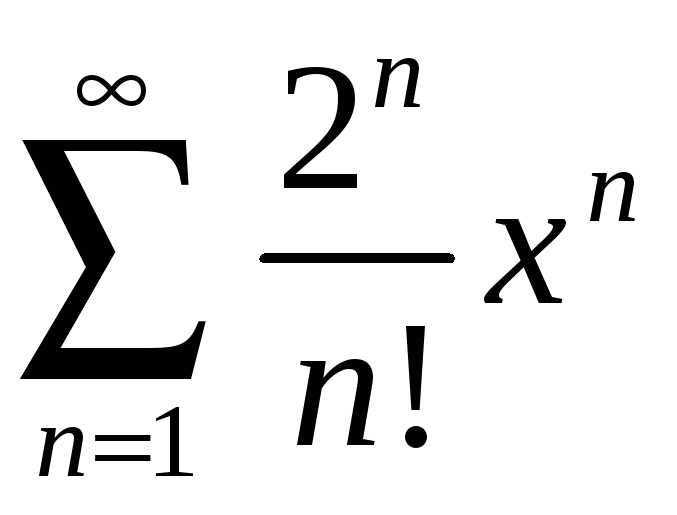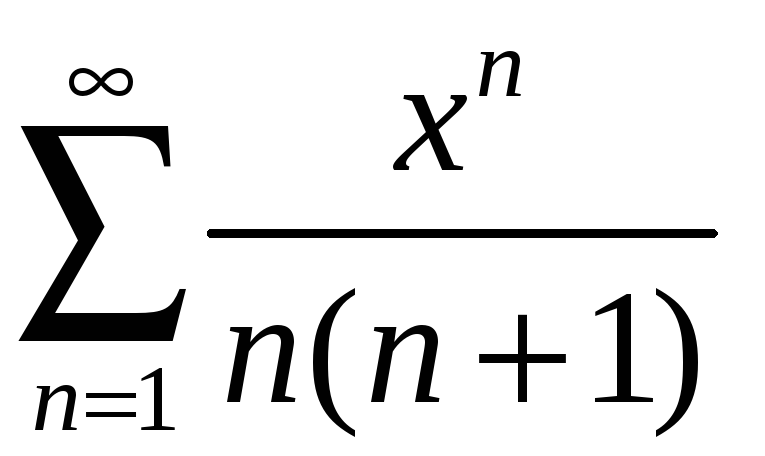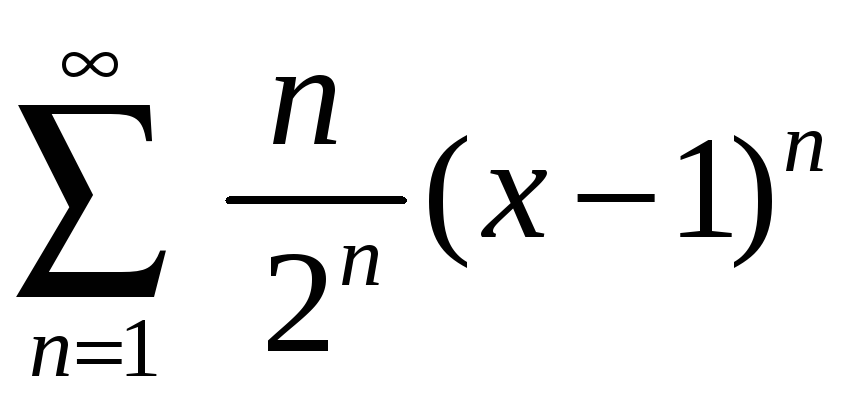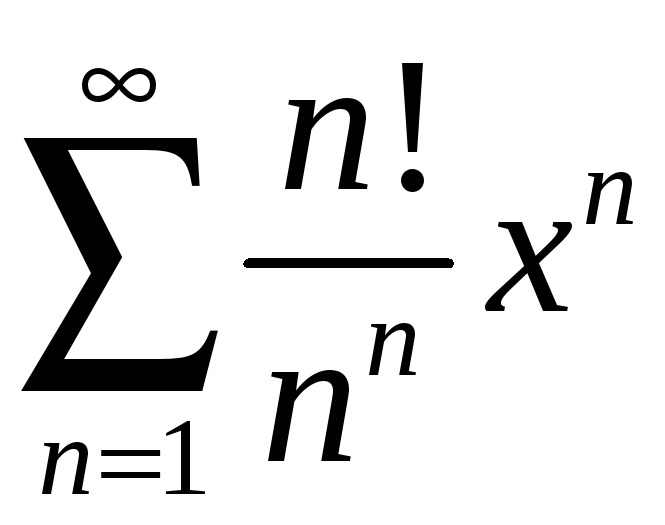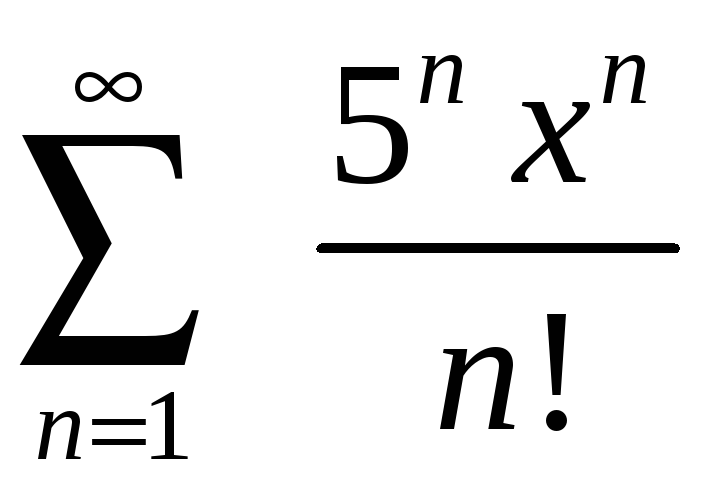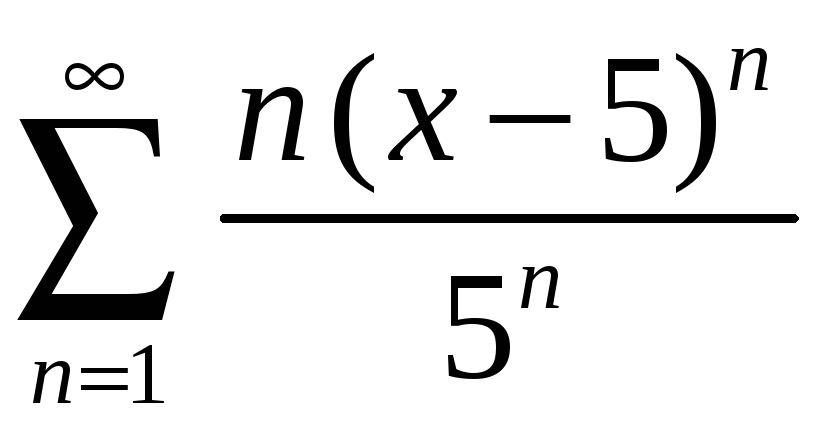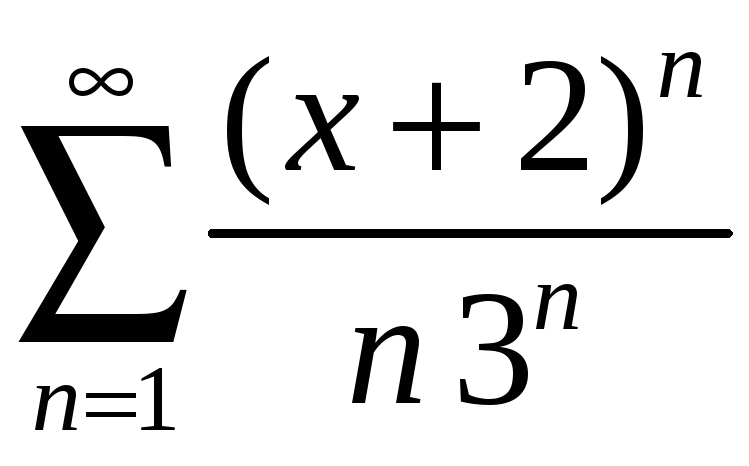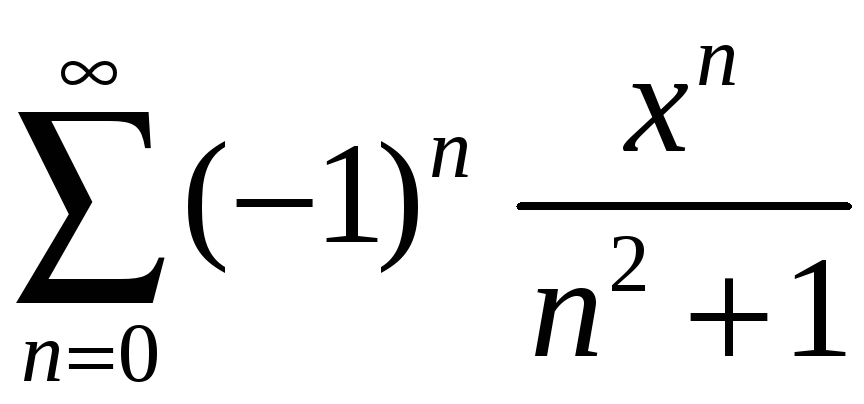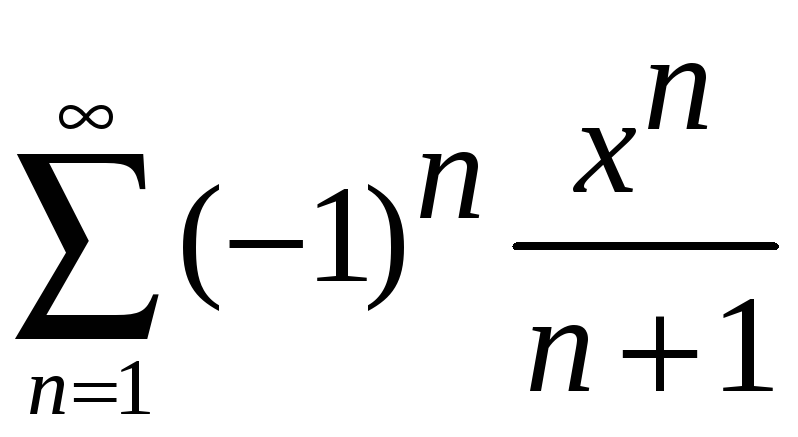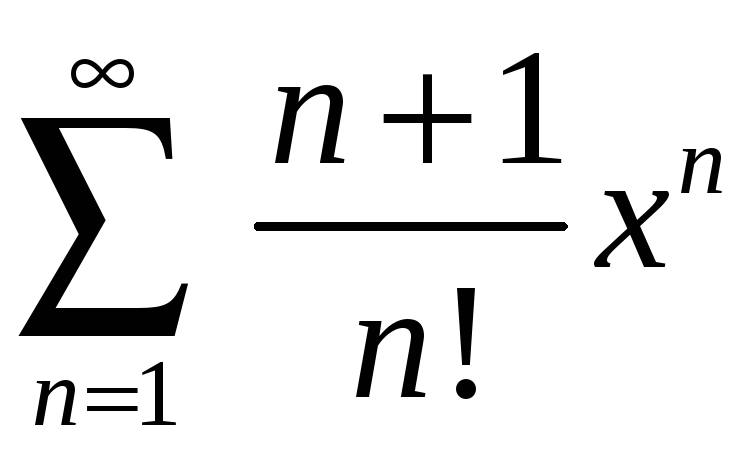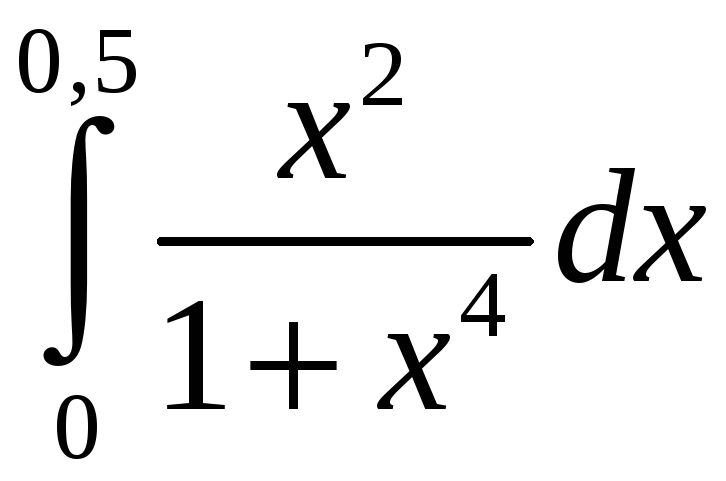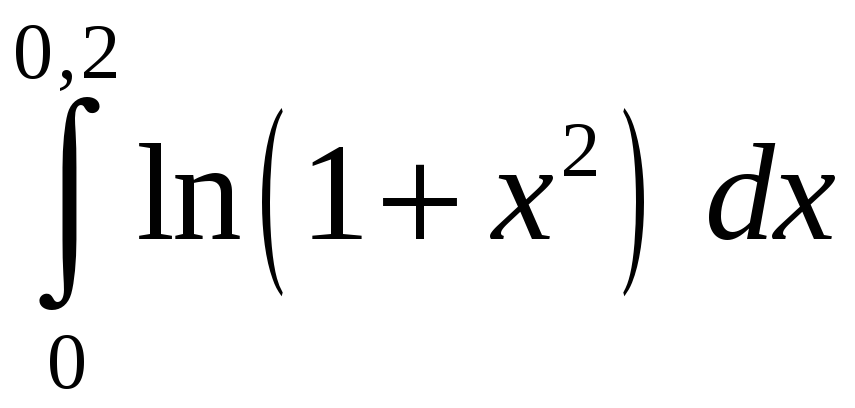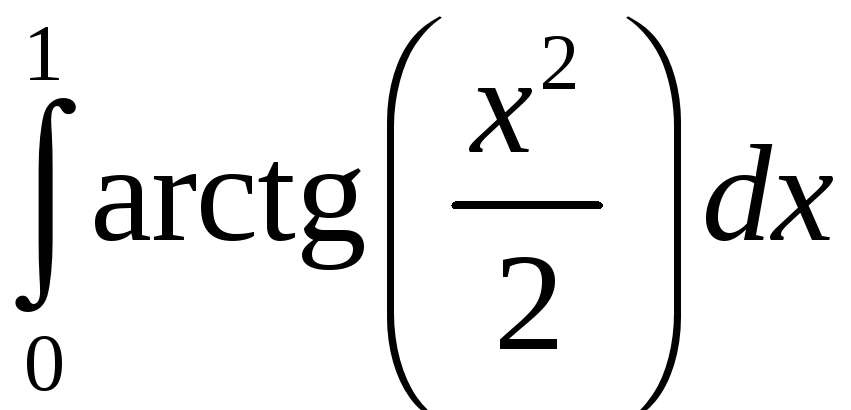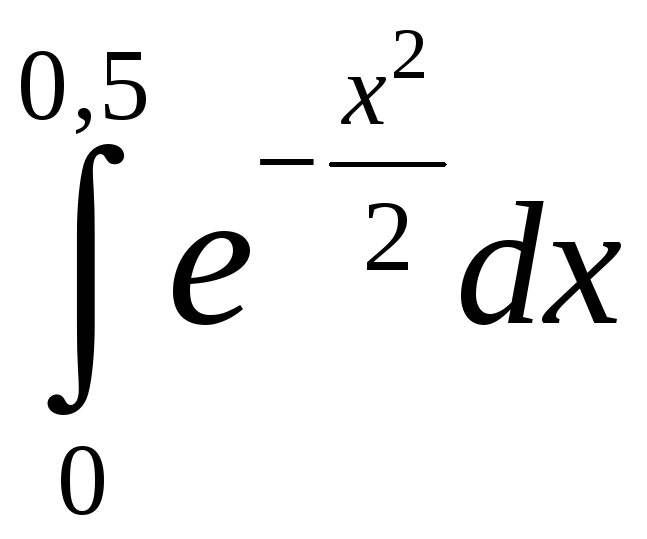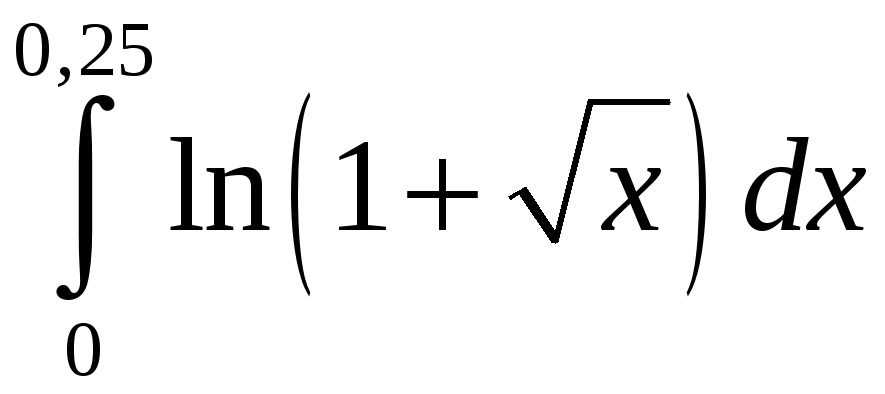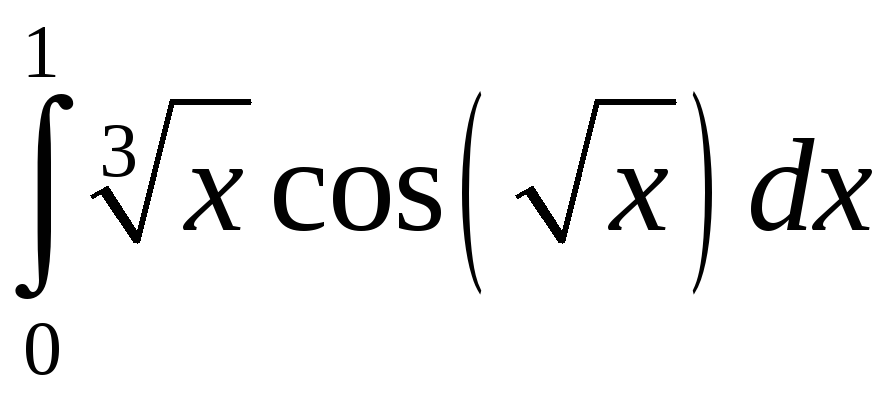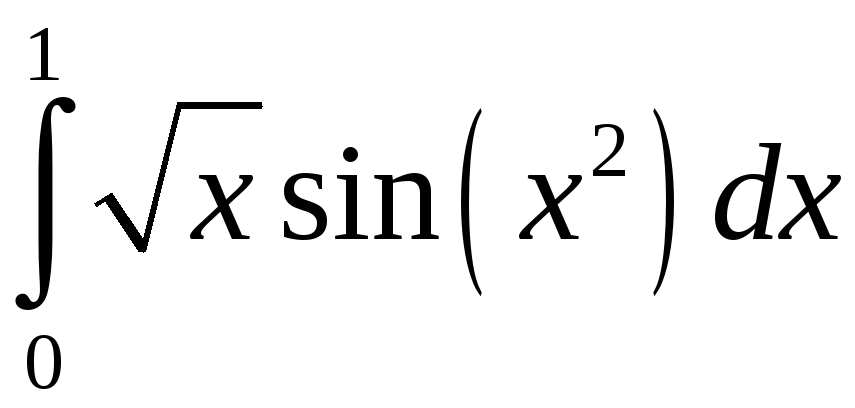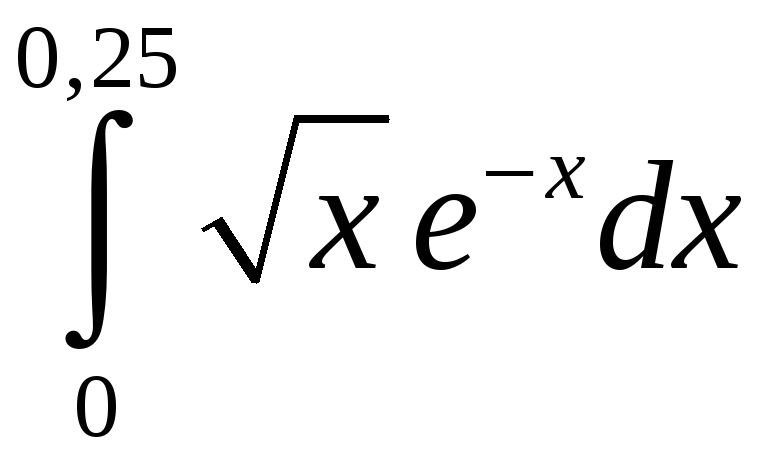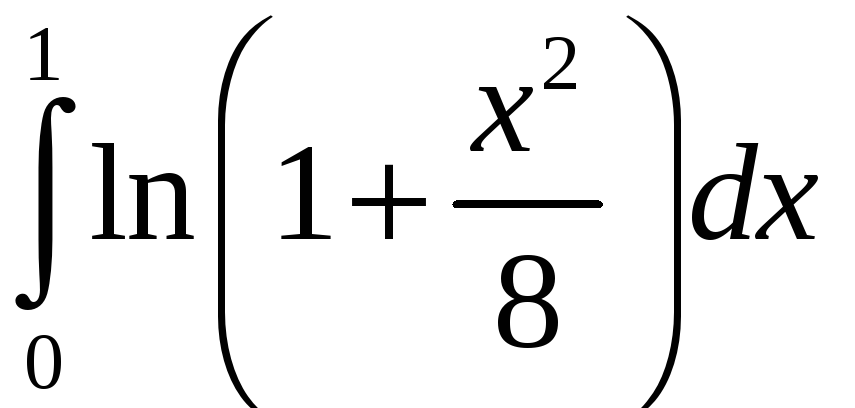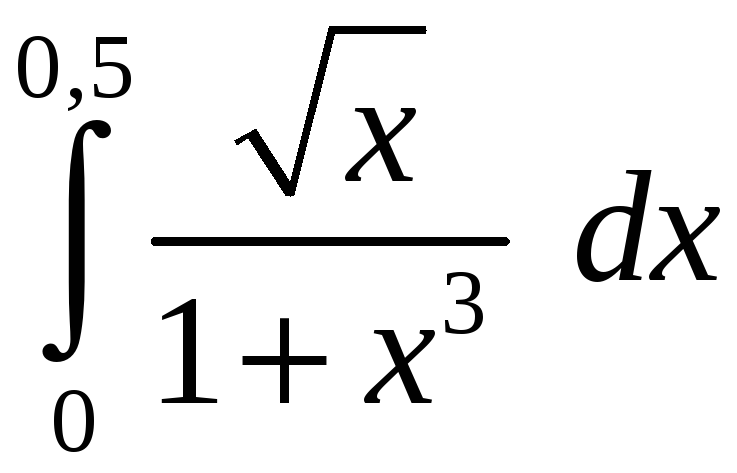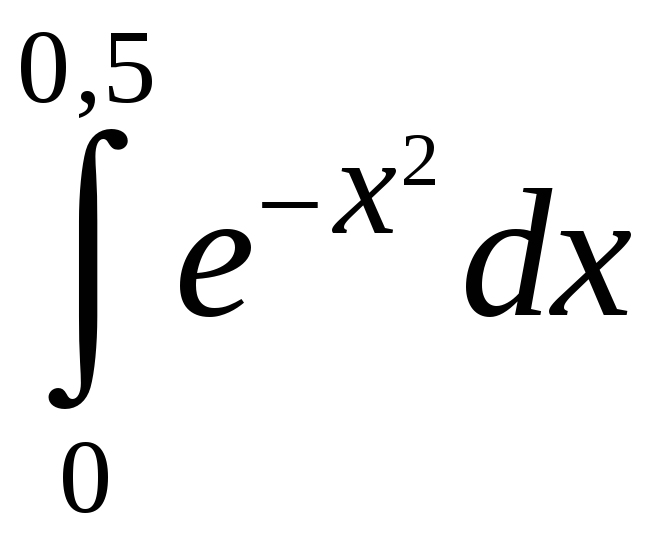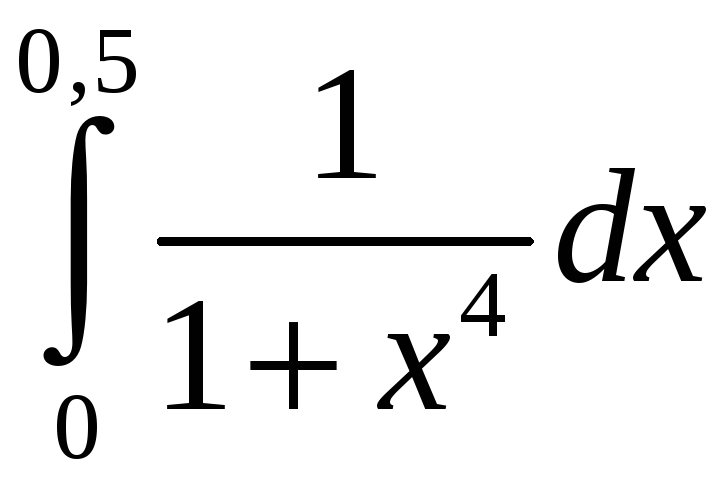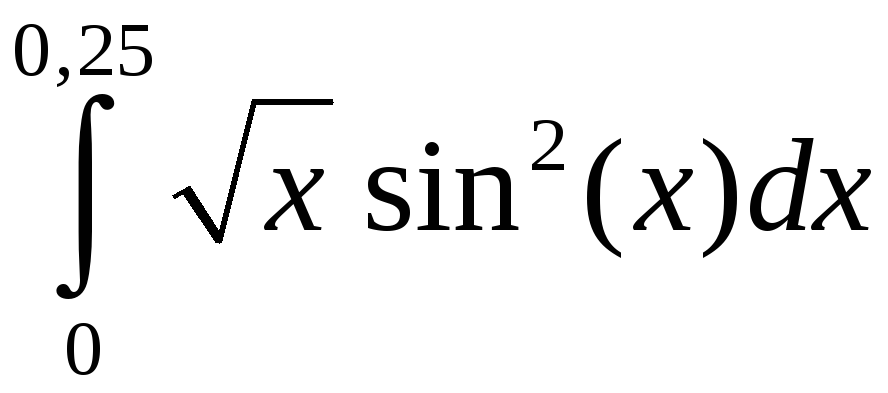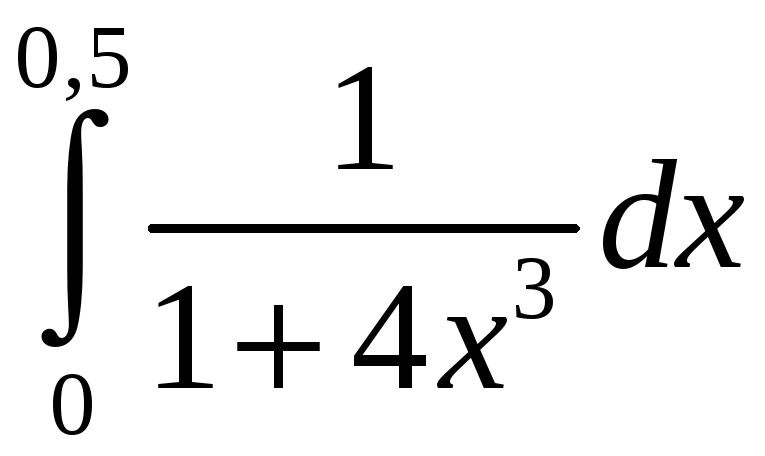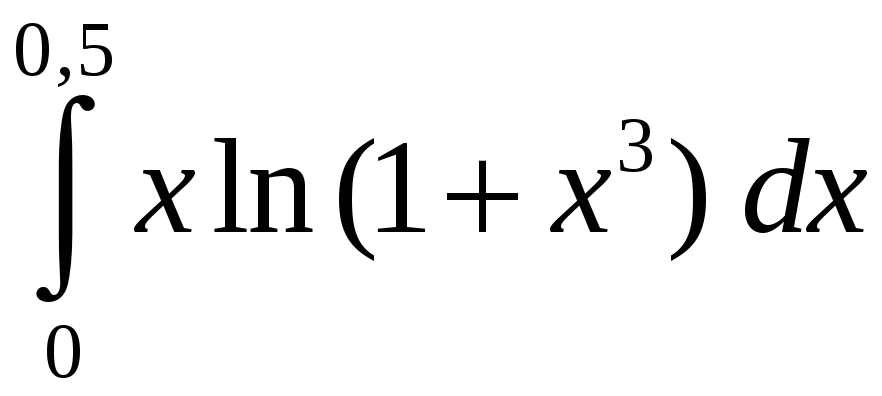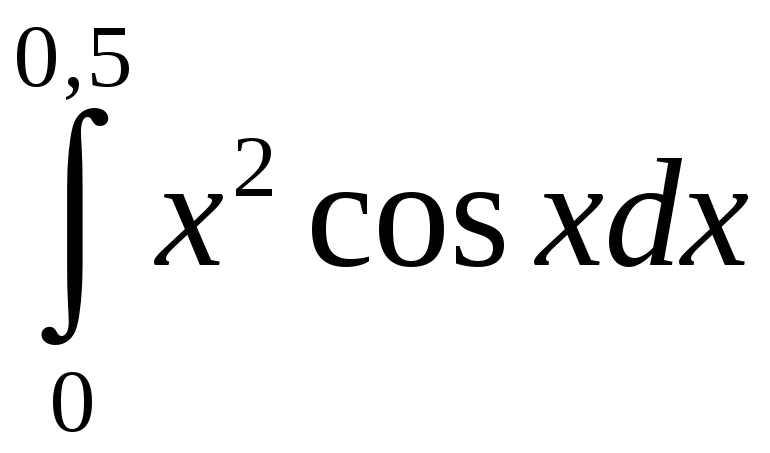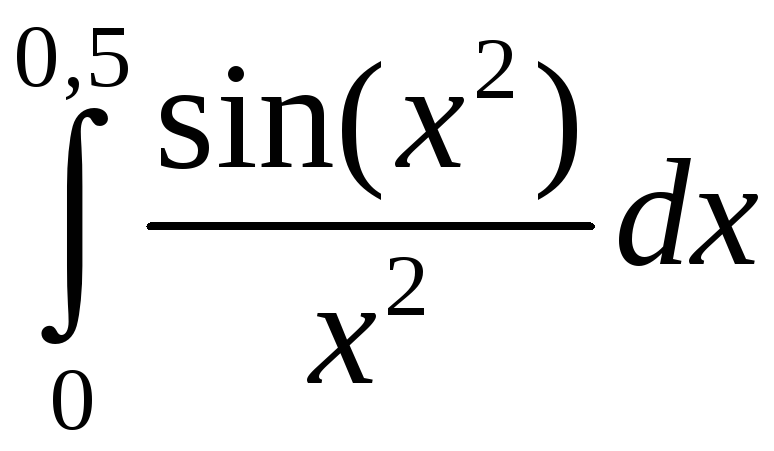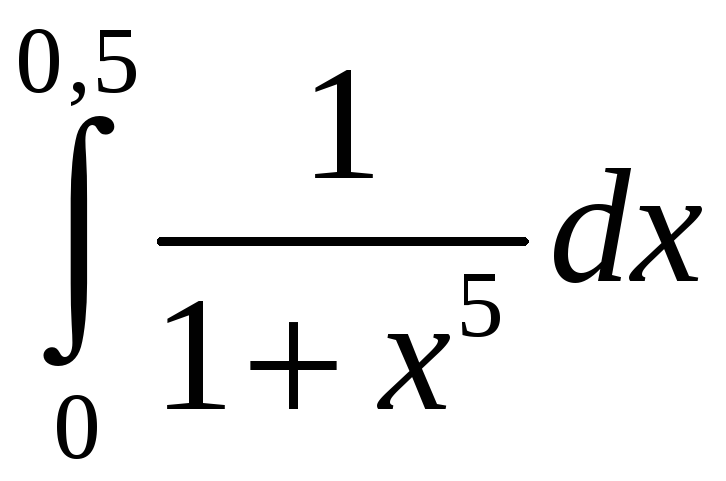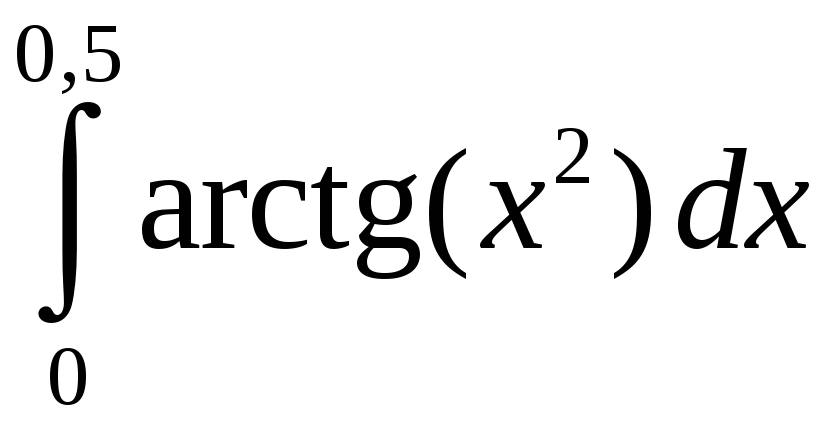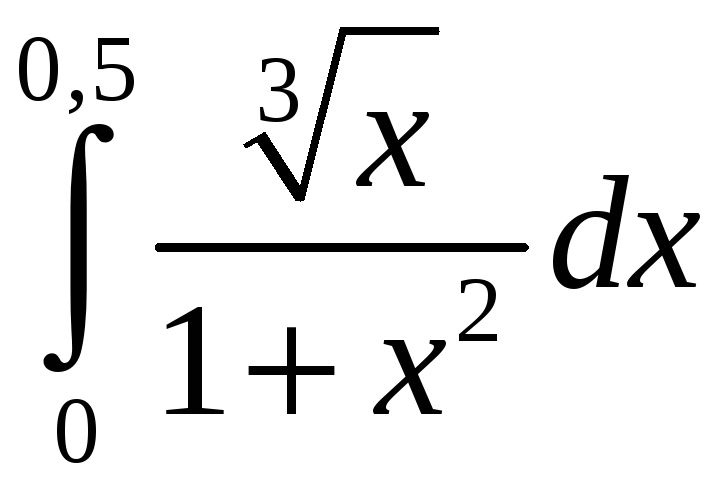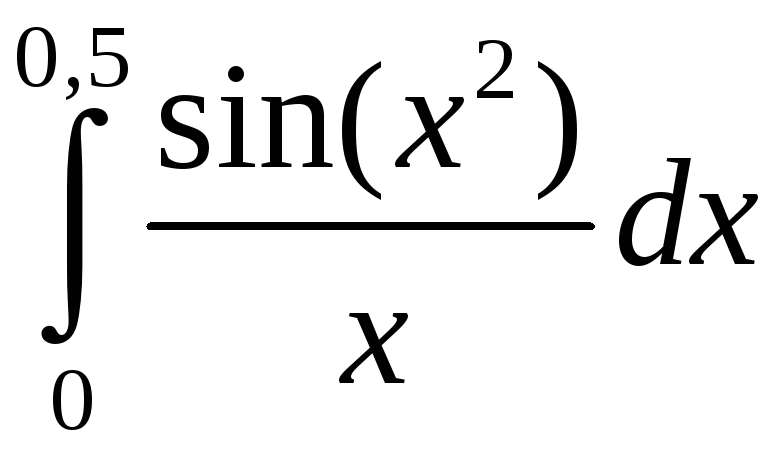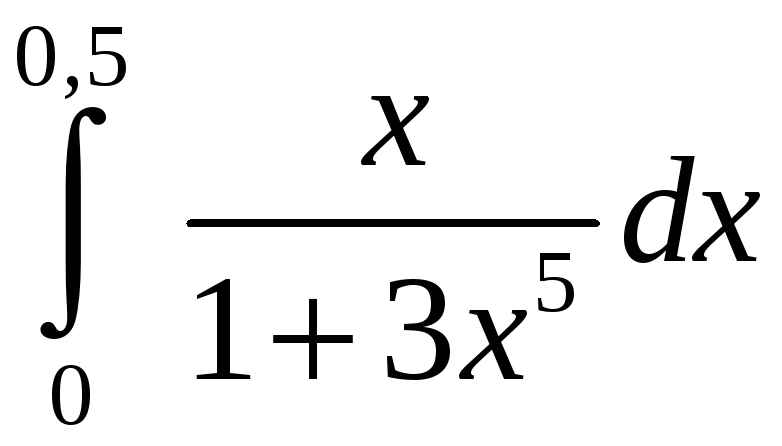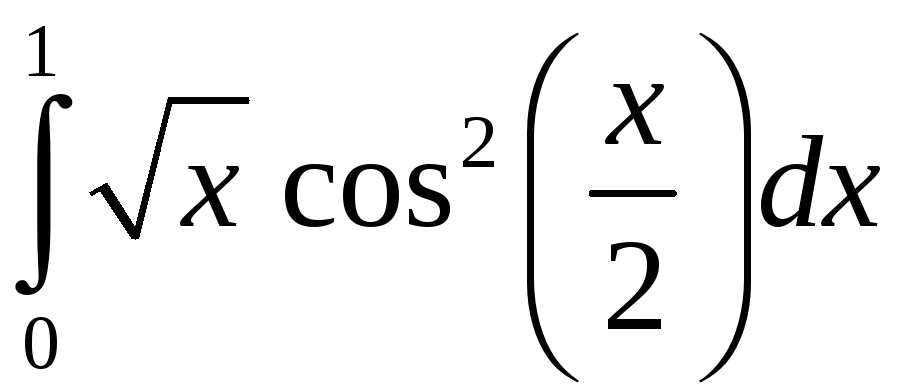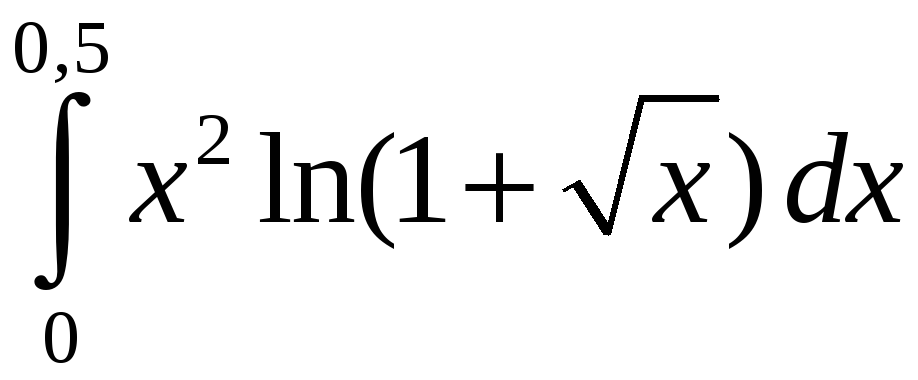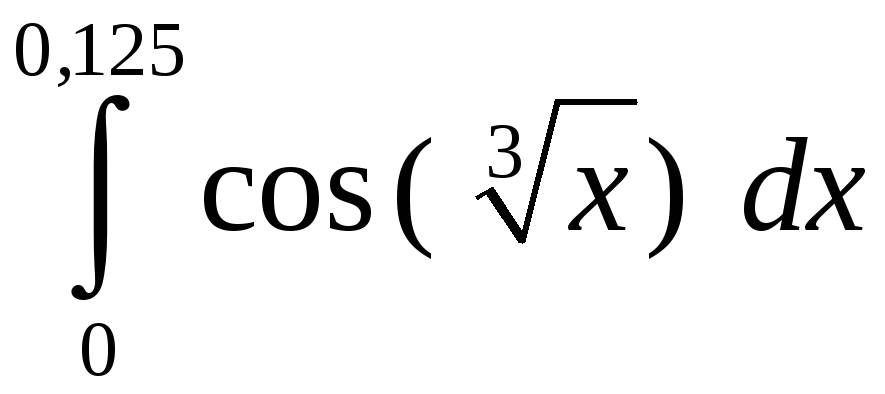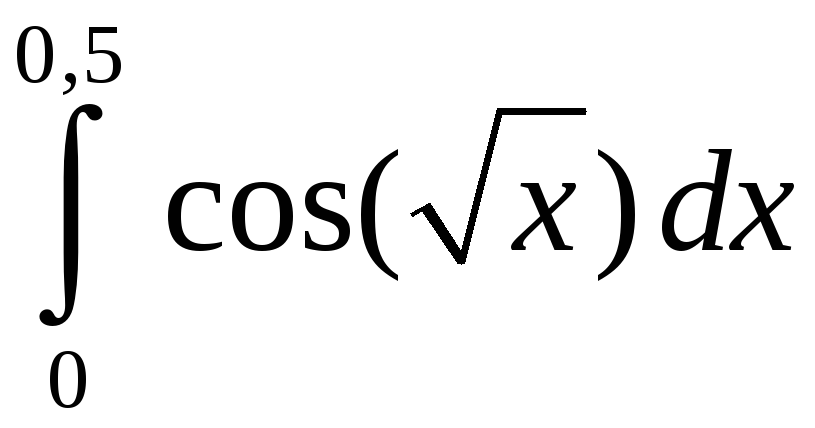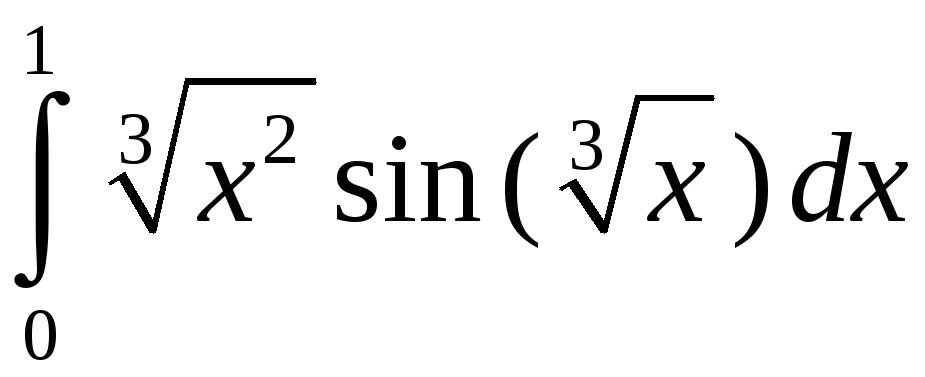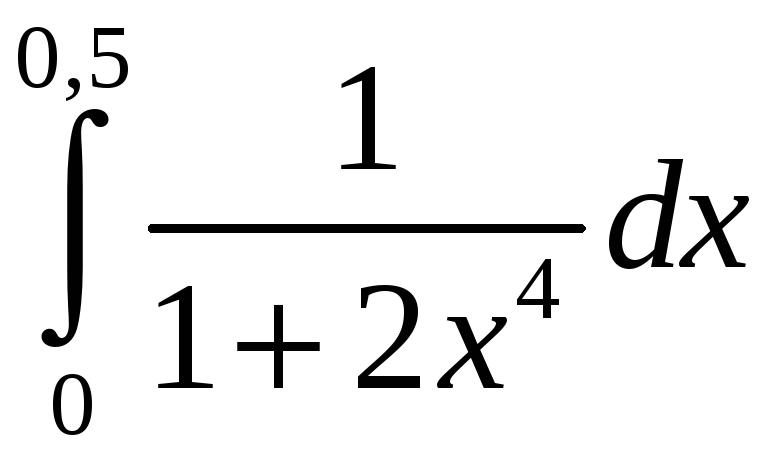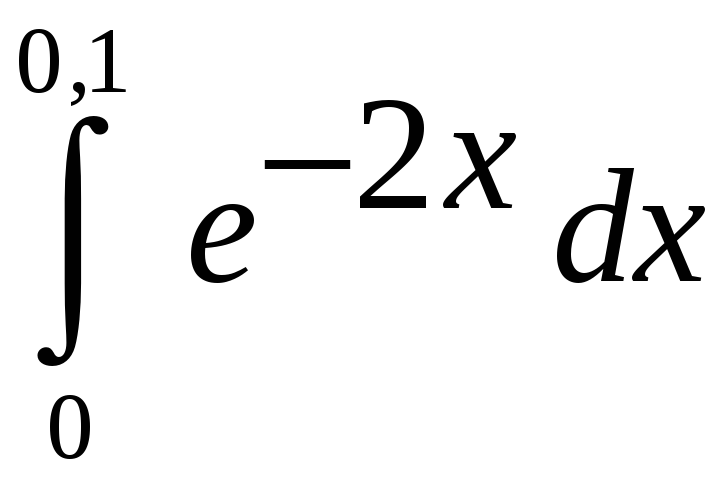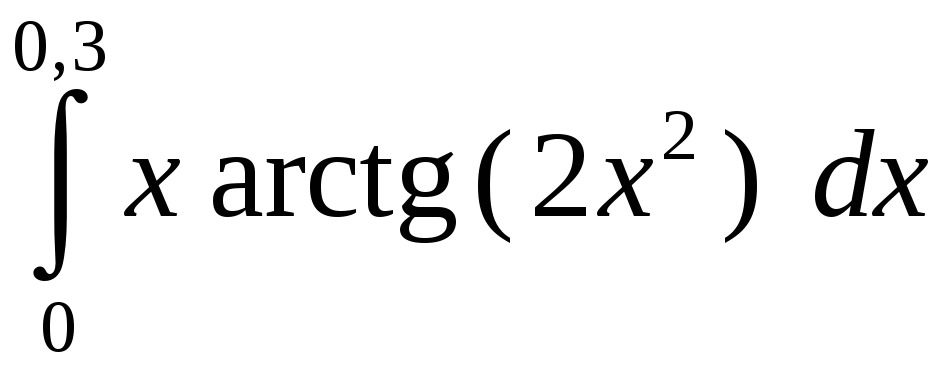матан ргз 2 семестр
.docУМКд-Т-МА-2-РГЗ
УТВЕРЖДЕНО
на заседании кафедры высшей математики
29 августа 2008 г., протокол №1
Зав.кафедрой _________________ Трофимов В.К.
Расчётно-графическое задание
по математическому анализу
1 курс 2 семестр
Задание 1. Найти неопределенные интегралы:
1)
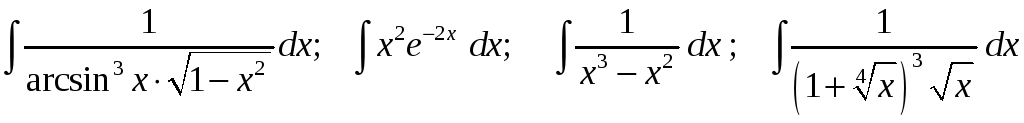
2)
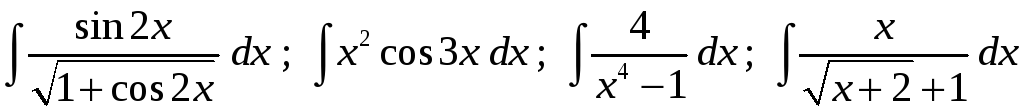
3)
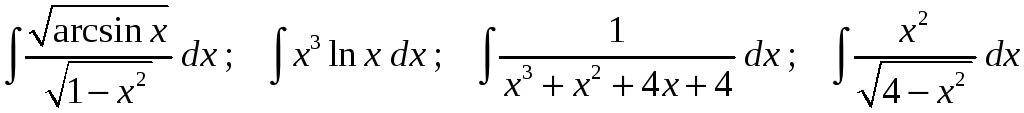
4)
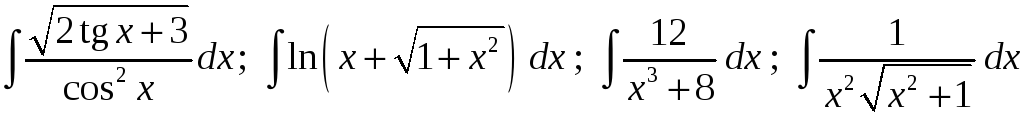
5)
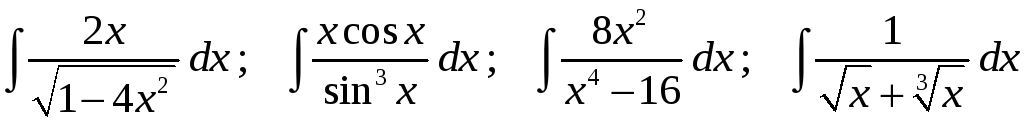
6)
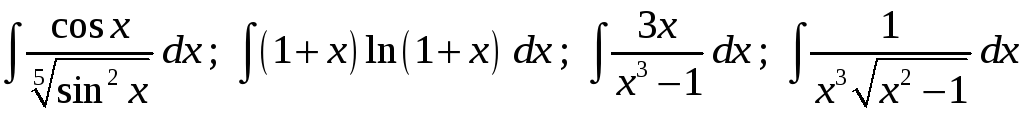
7)
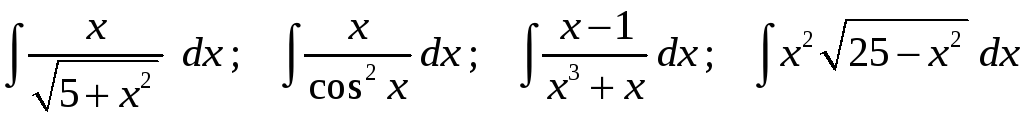
8)
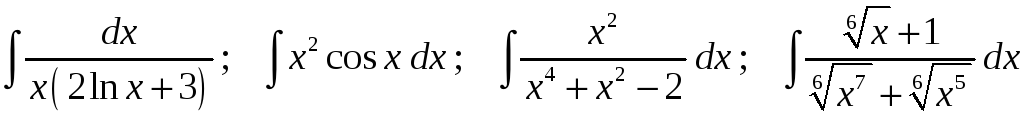
9)
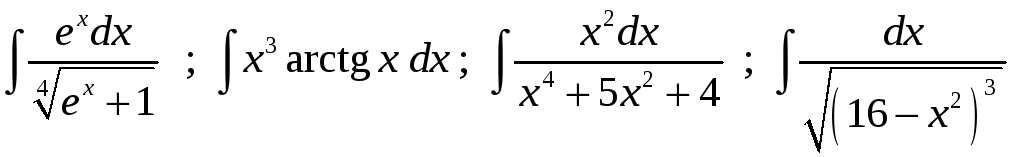
10)
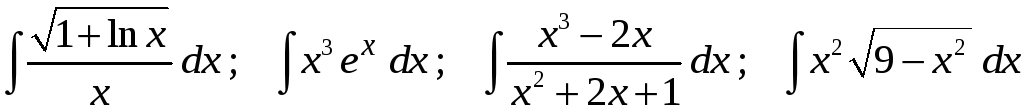
11)
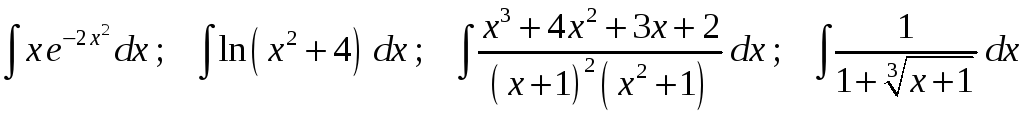
12)
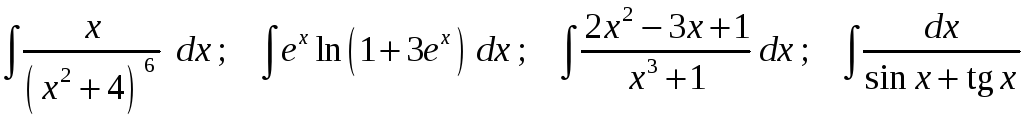
13)
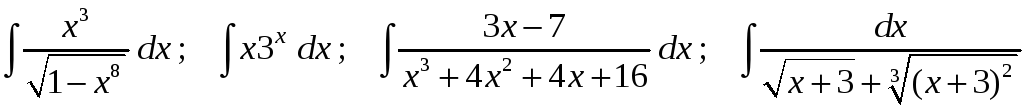
14)
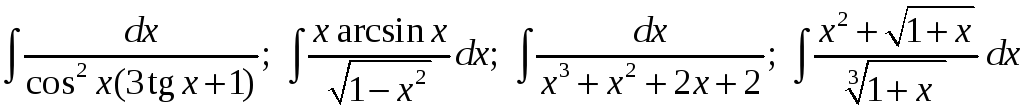
15)
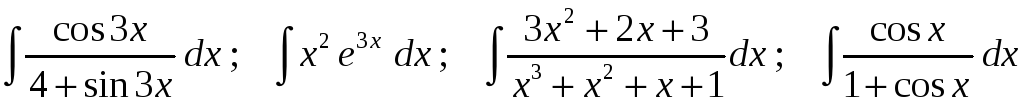
16)
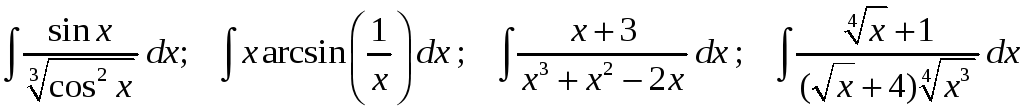
17)
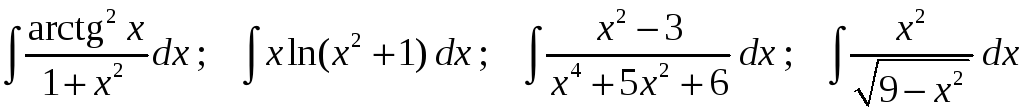
18)
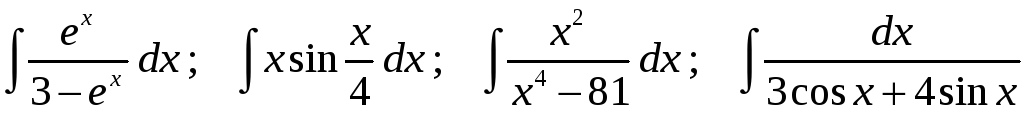
19)
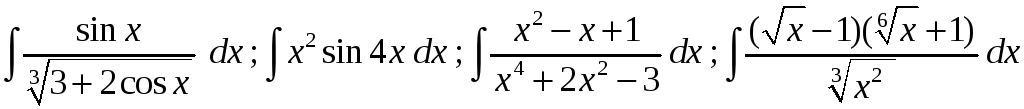
20)
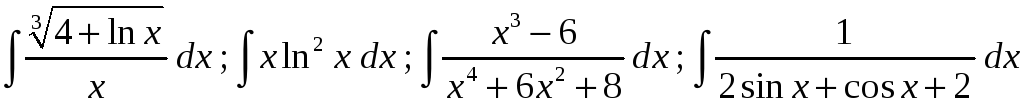
21)
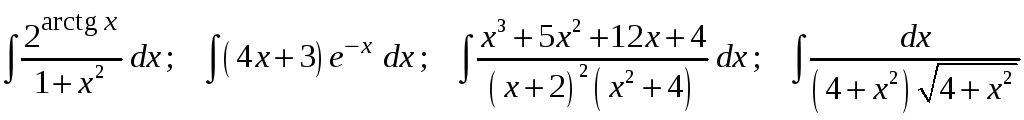
22)
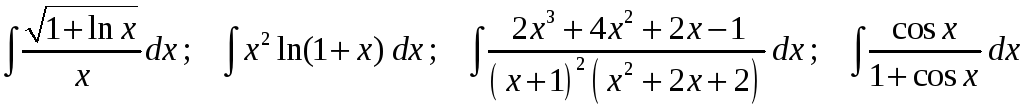
23)
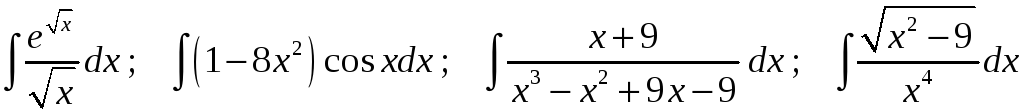
24)
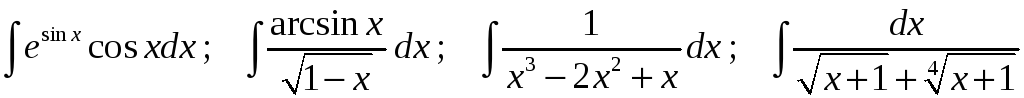
25)
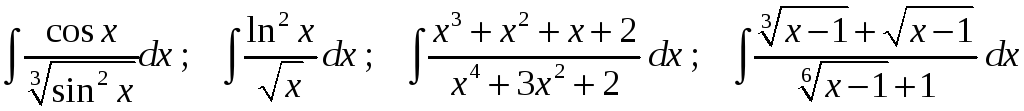
26)
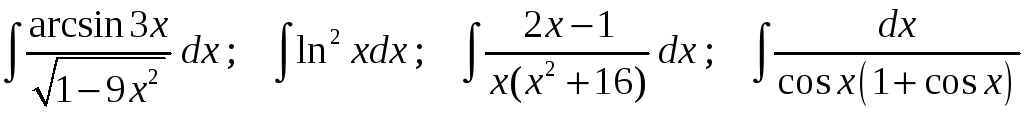
27)
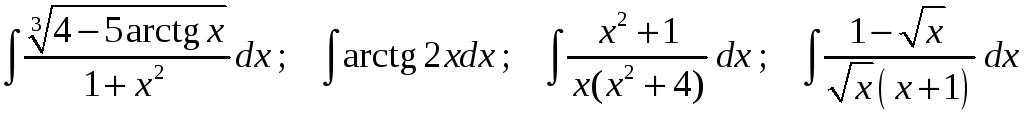
28)
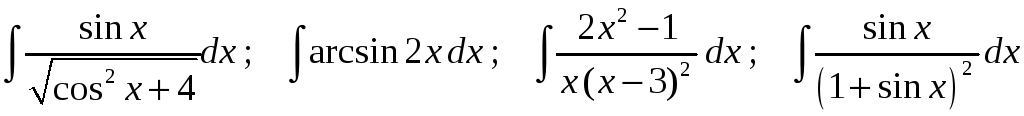
29)
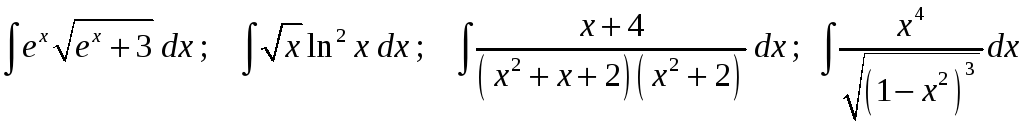
30)
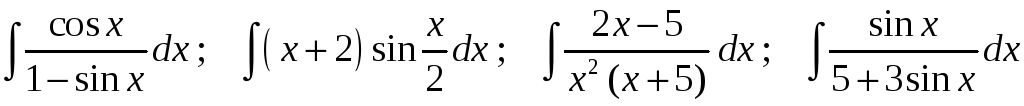
Задание 2. Найти площадь плоской фигуры, ограниченной линиями:
1)
![]() 2)
2)
![]()
3)
![]() 4)
4)
![]()
5)
![]() 6)
6)
![]()
7)
![]() 8)
8)
![]()
9)
![]() 10)
10)
![]()
11)
![]() 12)
12)
![]()
13)
![]() 14)
14)
![]()
15)
![]() 16)
16)
![]()
17)
![]() 18)
18)
![]()
19)
![]() 20)
20)
![]()
21)
![]() 22)
22)
![]()
23)
![]() 24)
24)
![]()
25)
![]() 26)
26)
![]()
27)
![]() 28)
28)
![]()
29)
![]() 30)
30)
![]()
Задание 3. Найти объём тела, ограниченного поверхностями:
1)
![]()
2)
![]()
3)
![]()
4)
![]()
5)
![]()
6)
![]()
7)
![]()
8)
![]()
9)
![]()
10)
![]()
11)
![]()
12)
![]()
13)
![]()
14)
![]()
15)
![]()
16)
![]()
17)
![]()
18)
![]()
19)
![]()
20)
![]()
21)
![]()
22)
![]()
23)
![]()
24)
![]()
25)
![]()
26)
![]()
27)
![]()
28)
![]()
29)
![]()
30)
![]()
Задание 4. Найти область сходимости ряда:
|
1)
2)
3)
4)
5)
6)
7)
8)
9)
10)
|
11)
12)
13)
14)
15)
16)
17)
18)
19)
20)
|
21)
22)
23)
24)
25)
26)
27)
28)
29)
30)
|
Задание 5. Вычислить с точностью до 0,001 интеграл, разлагая подынтегральную функцию в степенной ряд:
|
1)
2)
3)
4)
5)
6)
7)
8)
9)
10)
|
11)
12)
13)
14)
15)
16)
17)
18)
19)
20)
|
21)
22)
23)
24)
25)
26)
27)
28)
29)
30)
|
Задание 6.
Разложить функцию, заданную на отрезке
![]() ,
с периодом T
в ряд Фурье:
,
с периодом T
в ряд Фурье:
1)
![]() ,
,
![]() 2)
2)
![]() ,
,
![]()
3)
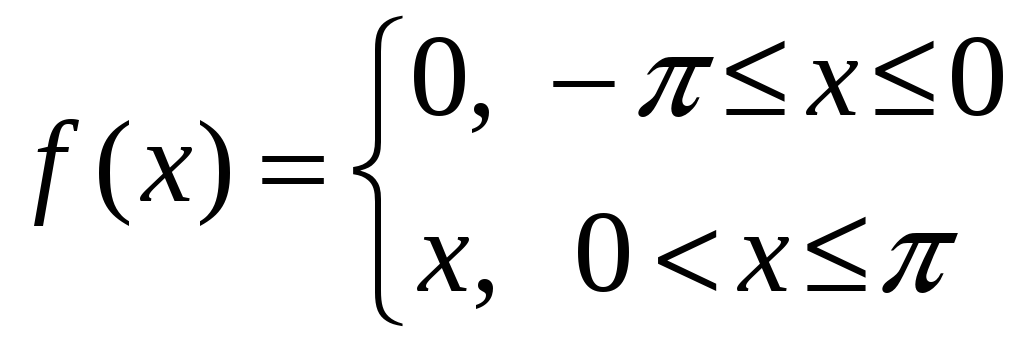 ,
,
![]() 4)
4)
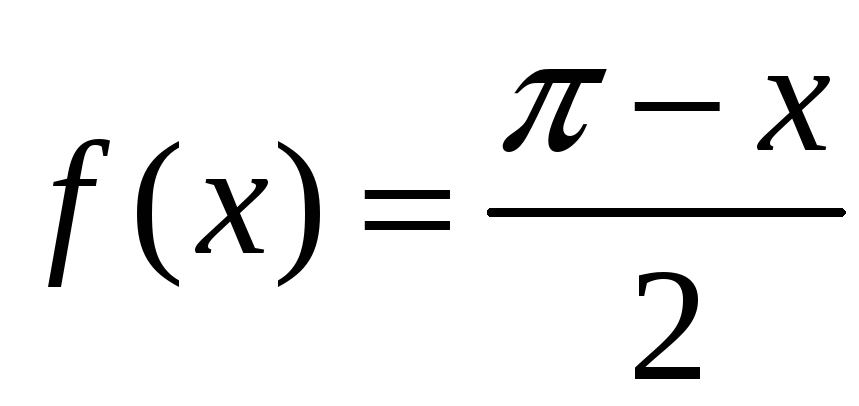 ,
,
![]() ,
,
![]()
5)
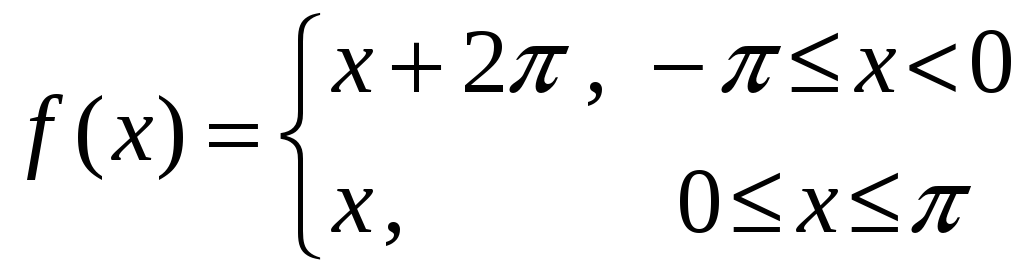 ,
,
![]() 6)
6)
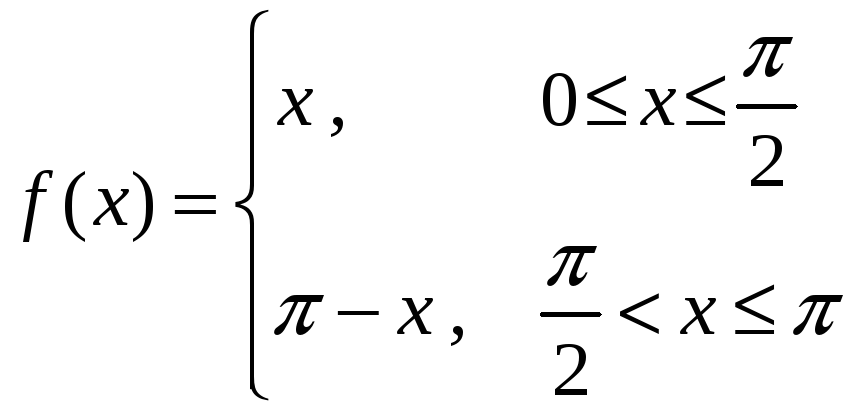 ,
,
![]()
7)
![]() 8)
8)
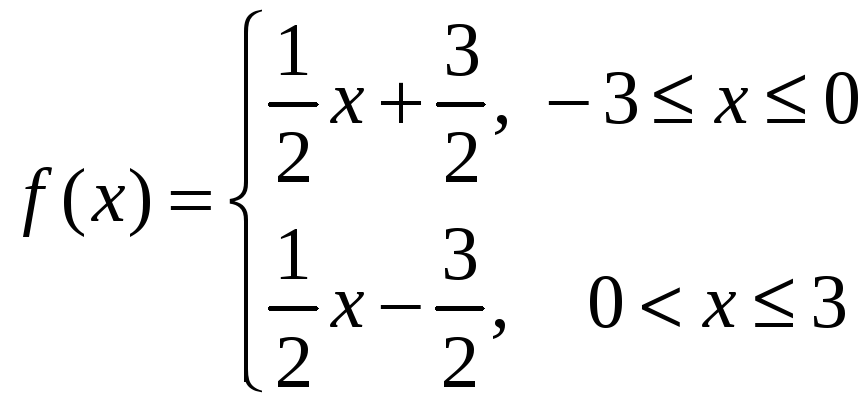 ,
,
![]()
9)
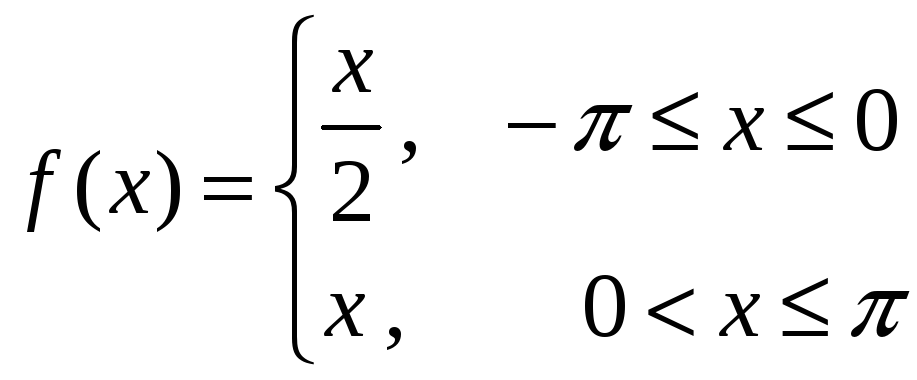 ,
,
![]() 10)
10)
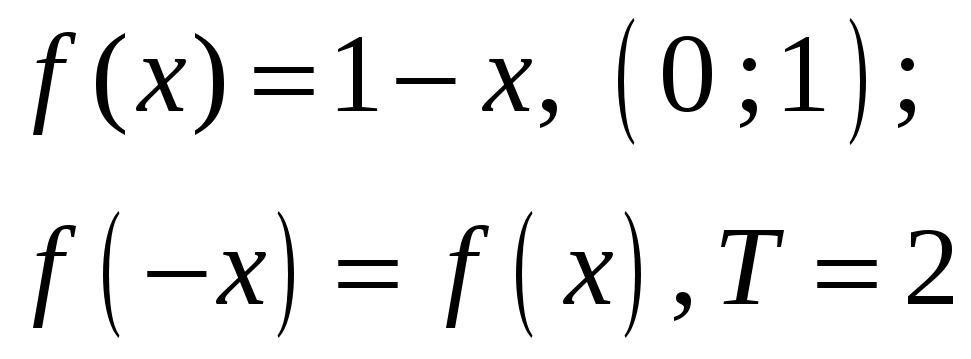 ,
,
11)
![]() ,
,
![]() 12)
12)
![]()
13)
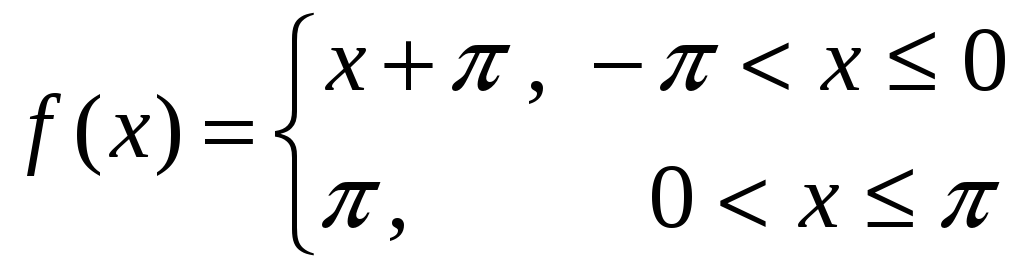 ,
,
![]() 14)
14)
![]()
15)
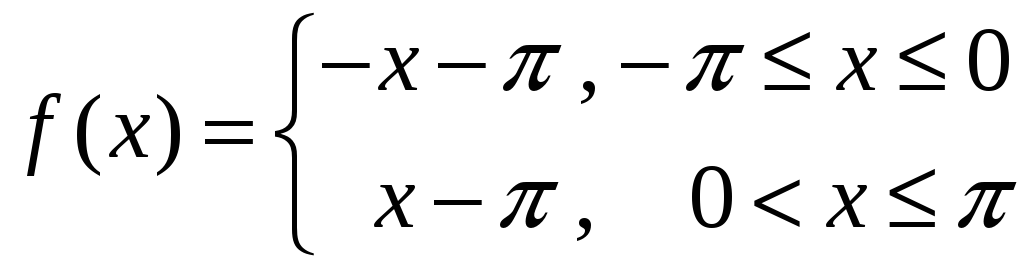 ,
,
![]() 16)
16)
![]()
17)
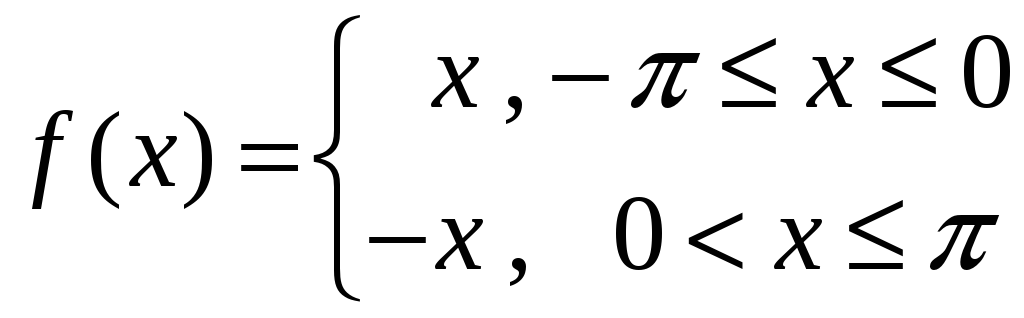 ,
,
![]() 18)
18)
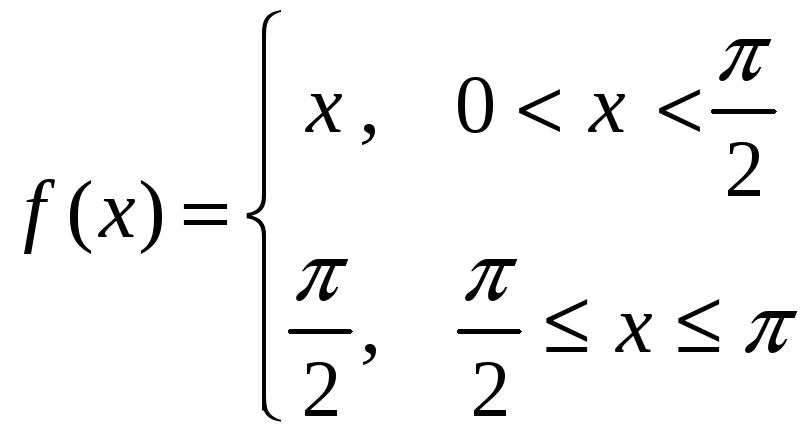 ,
,
![]()
19)
![]() ,
,
![]() 20)
20)
![]()
21)
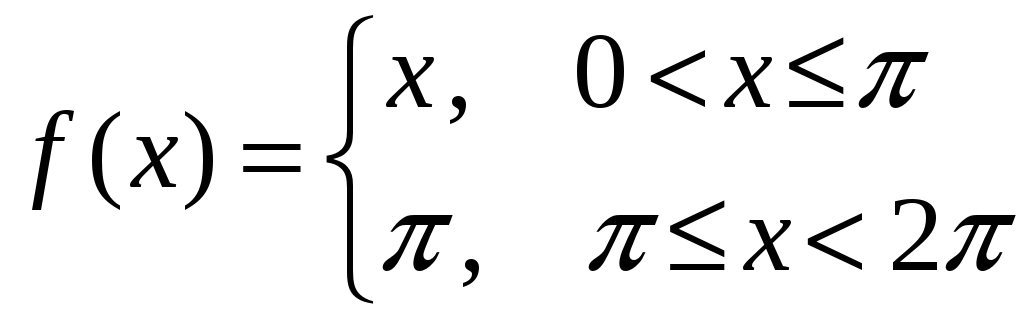 ,
,
![]() 22)
22)
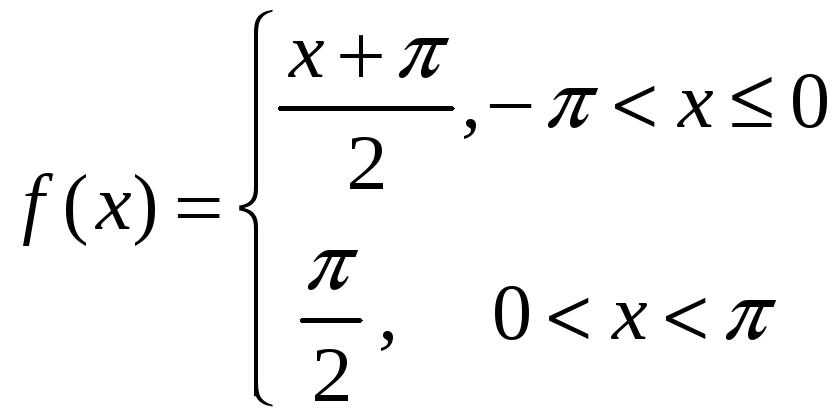 ,
,
![]()
23)
![]() 24)
24)
![]()
25)
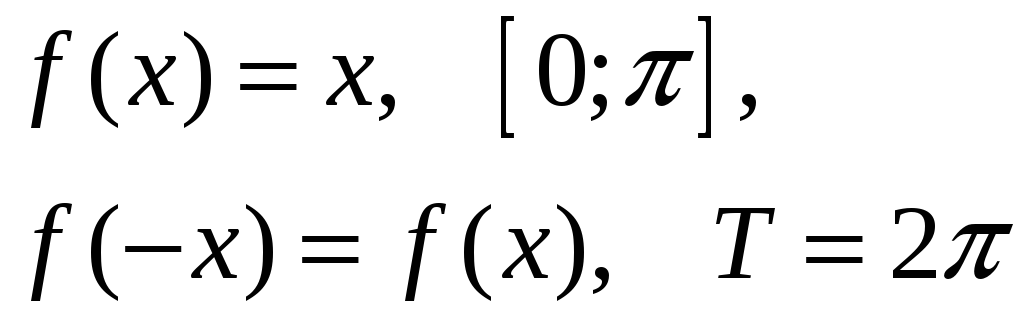 26)
26)
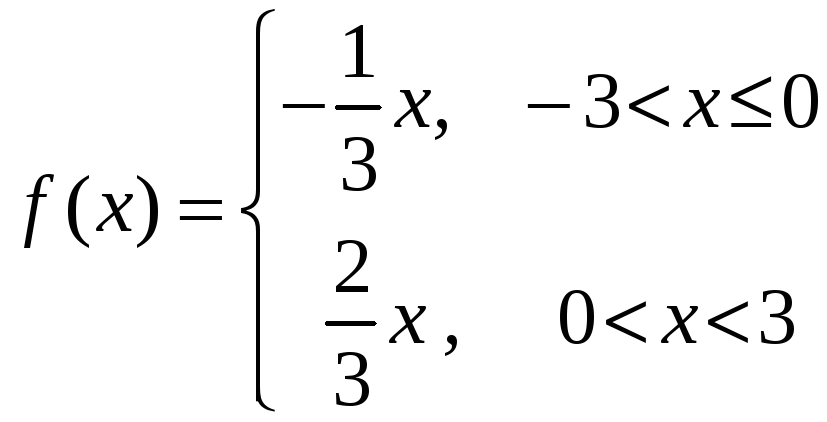 ,
,
![]()
27)
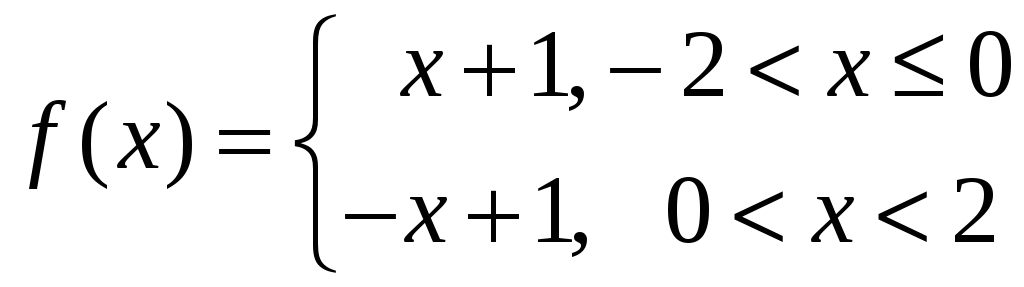 ,
,
![]() 28)
28)
![]()
29)
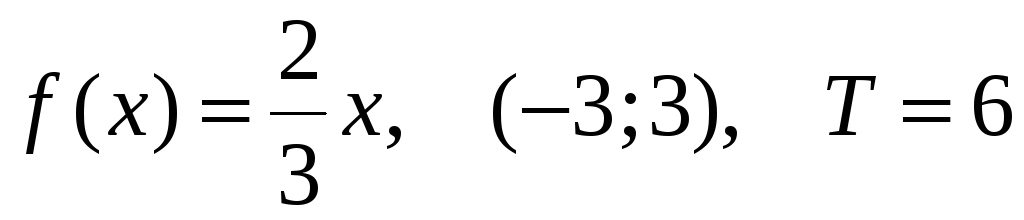 30)
30)
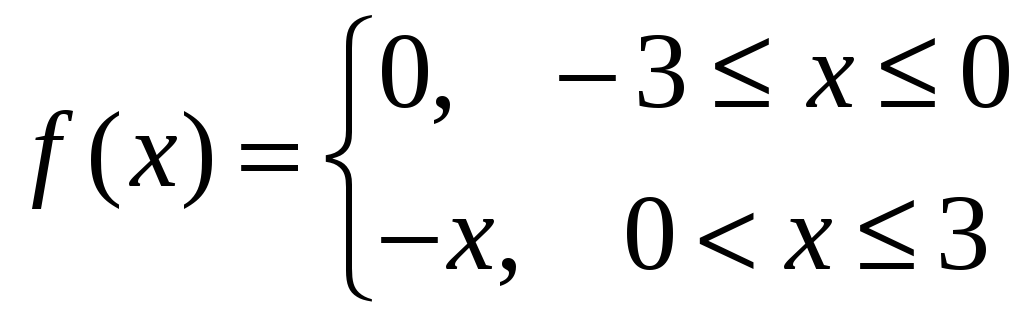 ,
,
![]()
Задание 7. Найти общее решение дифференциального уравнения:
1)
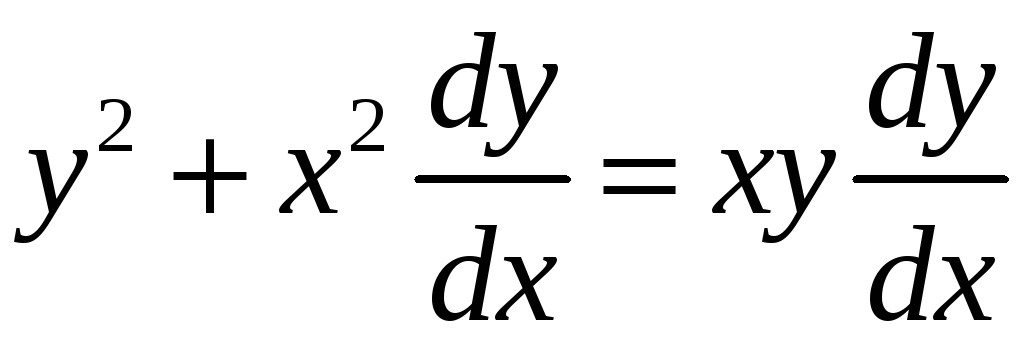
2)
![]()
3)
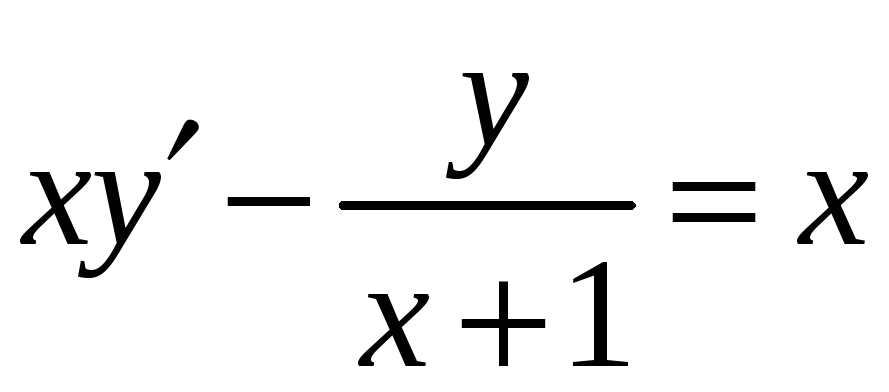
4)
![]()
5)
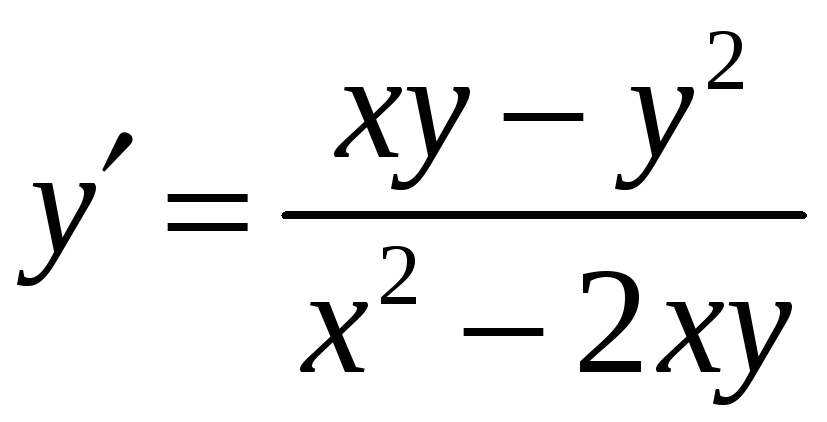
6)
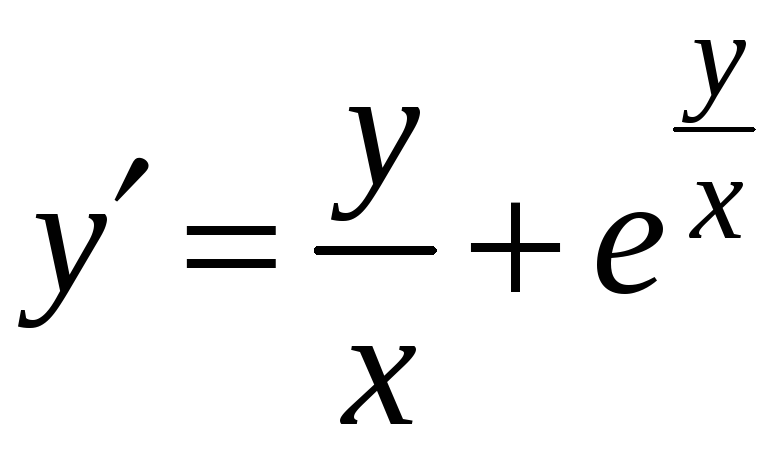
7)
![]()
8)
![]()
9)
![]()
10)
![]()
11)
![]()
12)
![]()
13)
![]()
14)
![]()
15)
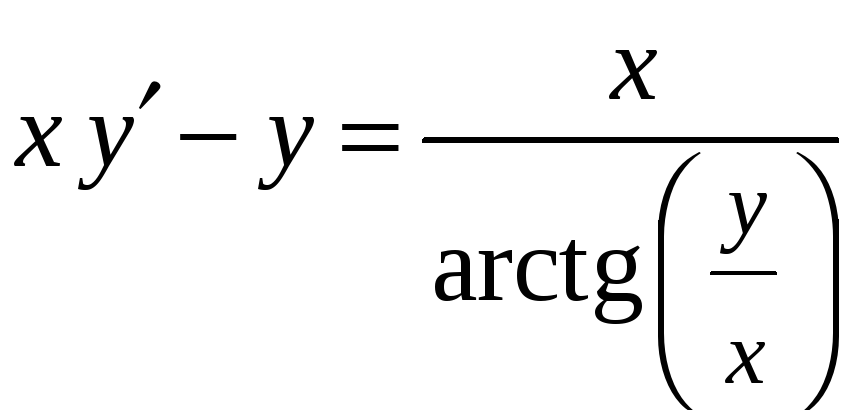
16)
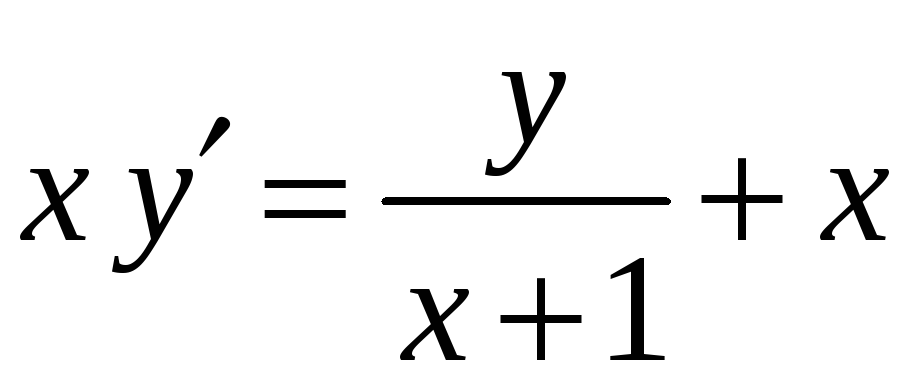
17)
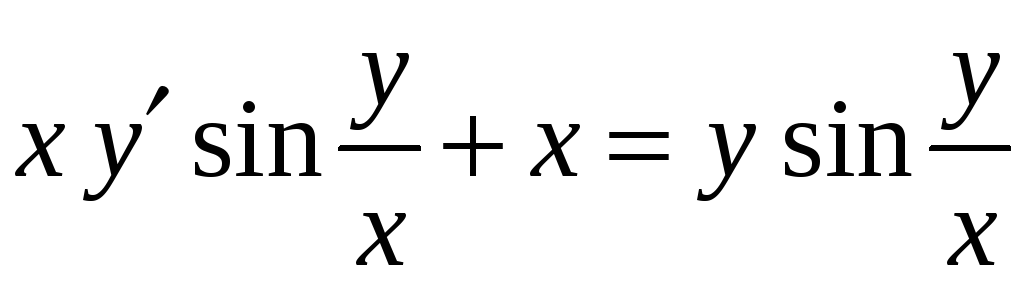
18)
![]()
19)
![]()
20)
![]()
21)
![]()
22)

23)
![]()
24)
![]()
25)
![]()
26)
![]()
27)
![]()
28)
![]()
29)
![]()
30)
![]()
Задание 8. Найти частное решение дифференциального уравнения, удовлетворяющего данному начальному условию:
1)
![]()
2)
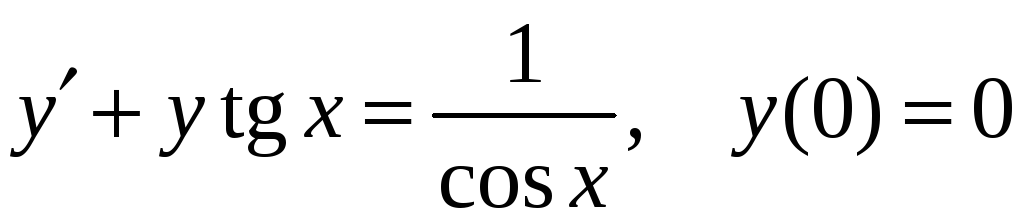
3)
![]()
4)
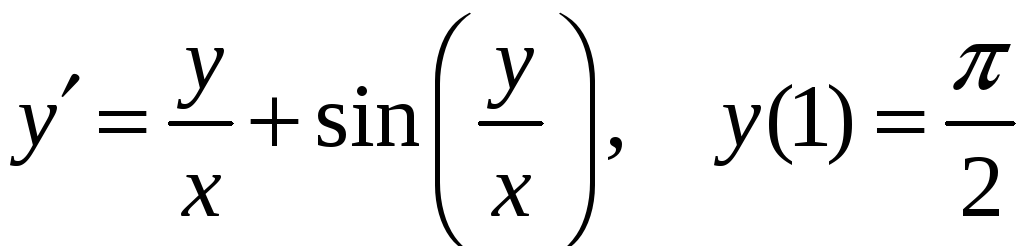
5)
![]()
6)
![]()
7)
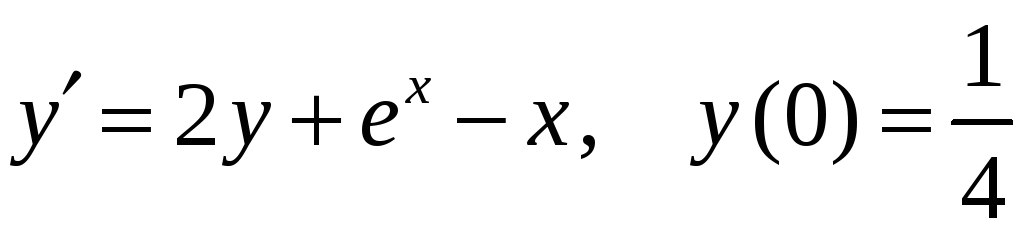
8)
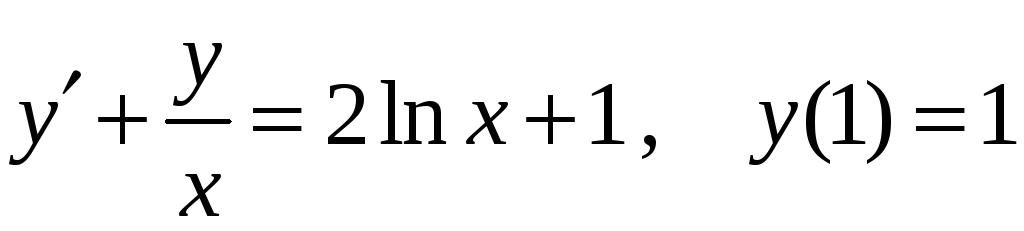
9)
![]()
10)
![]()
11)
![]()
12)
![]()
13)

14)
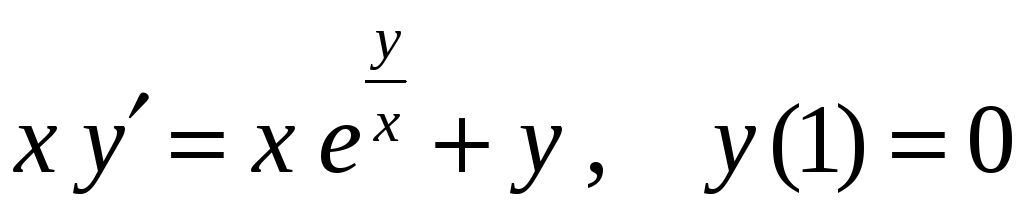
15)
![]()
16)
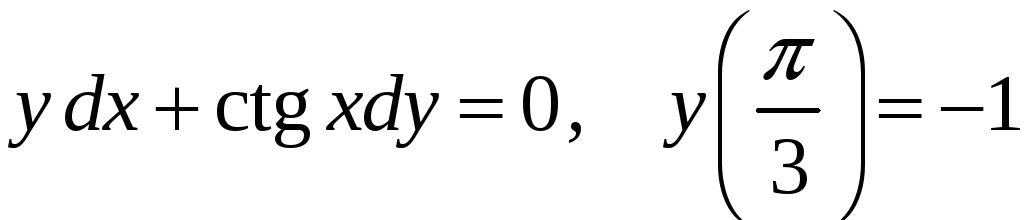
17)
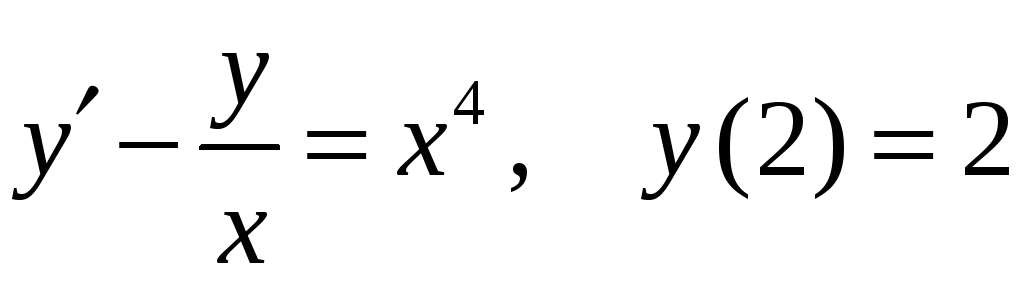
18)
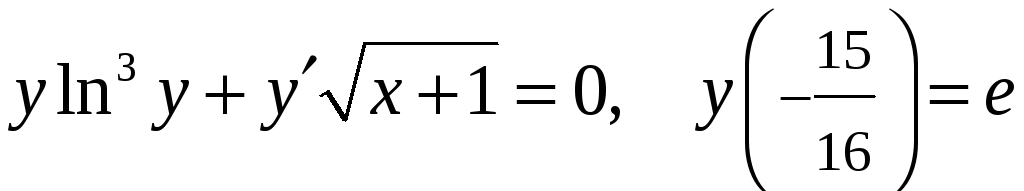
19)
![]()
20)
![]()
21)
![]()
22)
![]()
23)
![]()
24)
![]()
25)
![]()
26)
![]()
27)
![]()
28)
![]()
29)
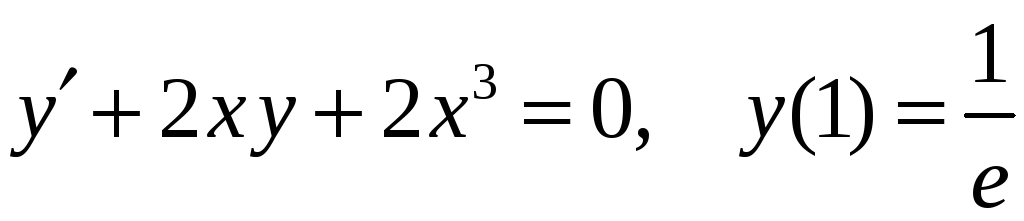
30)
![]()
Задание 9. Найти общее решение дифференциального уравнения:
1)
![]() 2)
2)
![]()
3)
![]() 4)
4)
![]()
5)
![]() 6)
6)
![]()
7)
![]() 8)
8)
![]()
9)
![]() 10)
10)
![]()
11)
![]() 12)
12)
![]()
13)
![]() 14)
14)
![]()
15)
![]() 16)
16)
![]()
17)
![]() 18)
18)
![]()
19)
![]() 20)
20)
![]()
21)
![]() 22)
22)
![]()
23)
![]() 24)
24)
![]()
25)
![]() 26)
26)
![]()
27)
![]() 28)
28)
![]()
29)
![]() 30)
30)
![]()