10. Медиана интервального вариационного ряда

,(20)

где – нижняя граница медианного интервала;– величина медианного интервала;– накопленная частота (или частость) интервала, предшествующего медианному;– половина суммы всех частот (или частостей);– частота медианного интервала.

При исчислении медианы интервального вариационного ряда сначала находят интервал, содержащий медиану. Для этого используют накопленные частоты (или частости). Медианному интервалу соответствует первая из накопленных частот (или частостей), превышающая половину всего объёма совокупности.

Пример: процент выполнения норм выработки (х).

Интервалы	xi	mi	Накопленные частоты
90–100	95	3	3
100–110	105	8	11
110–120	115	7	18
120–130	125	2	20
Σ	–	20	–

Первая из накопленных частот превышает 0,5·Σm_i, т.е. 10:

0,5·Σm_i, = 10.

Значит медианный интервал (100–110):

= 100; = 3;

k = 100 – 100 = 10; = 3;

11. Мода

В математической статистике модой называют вариант, наиболее часто встречающийся в данном вариационном ряду.

Для дискретного ряда мода определяется по наибольшей частоте и соответствует варианту с наибольшей частотой.

Мода для непрерывного (интервального с равными интервалами) ряда исчисляется по формуле:

,(21)

где х_Мо(min) - нижняя граница модального интервала;

m_Мо - частота модального интервала;

m_Мо–1 - частота интервала, предшествующего модальному;

m_Мо+1 - частота интервала, последующего за модальным;

k_i - величина модального интервала.

Может быть: одна мода – унимодальное распределение;

две моды – бимодальное распределение;

три и более – мультимодальное распределение.

Модальный интервал определяется по набольшей частоте.

Пример:

Интервалы	mi
90–100	3
100–110	8
110–120	7
120–130	2
Σ	20

Модальный интервал (100–110), т.к. он имеет наибольшую частоту.

х_Мо(min) = 100

k = 10 m_Мо–1 = 3;

m_Мо = 8; m_Мо+1 = 7;

Мо ≈108,3

Показатели колеблемости (вариации) признака

Такие признаки, как заработная плата, профессия, число членов семьи, возраст и т.д. — варьируют.

Для измерения вариации признака математическая статистика применяет ряд показателей.

12. Вариационный размах (R), или широта распределения

R = x_max – x_min (22)

применялся в формуле (8.6)

x_max — наибольший вариант вариационного ряда.

x_min — наименьший вариант вариационного ряда.

R представляет собой величину неустойчивую, зависящую от случайных обстоятельств. Она применяется в качестве приблизительной оценки вариации.

Среднее линейное отклонение

невзвешенное

взвешенное (23)

13 Дисперсия (средний квадрат отклонения)

невзвешенная

взвешенная (24)

Упрощённая формула дисперсии

, (25)

где

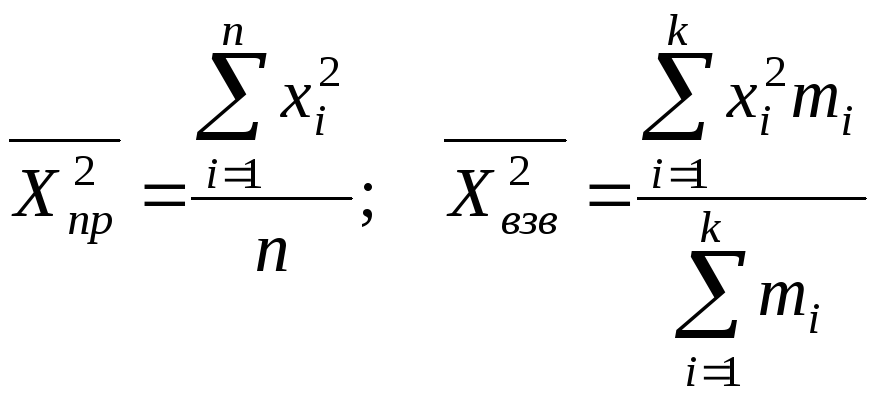
14. Среднее квадратическое отклонение (с.к.о.)

(26)

15. Коэффициент вариации (υ)

(27)

Применяется только для признака, принимающего только положительные значения.

Если ν > 40%, то это говорит о большой колеблемости признака в изучаемой совокупности (например большая колеблемость товарооборота в регионе).

–коэффициент осцилляции

–коэффициент вариации по среднему линейному отклонению.

16. Свойства дисперсии

1. σ²(С) = 0, где С – const.

2. Если все значения вариантов признака Х уменьшить на постоянную величину, то дисперсия не изменится.

3. Если все значения вариантов признака Х увеличить в k раз, то дисперсия увеличится в k² раз.

4. Вычисление дисперсии методом отсчёта от условного нуля (методом моментов).

(28)

17. Частные средние и частные дисперсии

Пусть вся совокупность разбита на l групп. Для каждой группы вариантов вариационного ряда можно вычислить средние, которые называются частными средними и дисперсии, которые называются частными дисперсиями или внутригрупповыми дисперсиями. Пусть l групп:

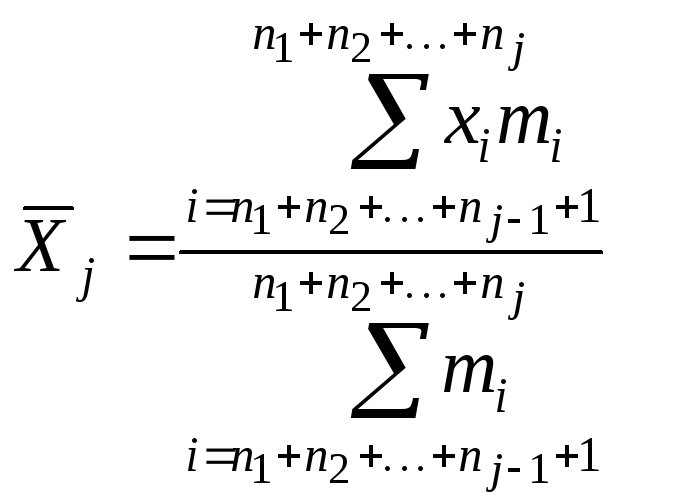(29)

j=1, 2, …, l;

Σm_i = N_j – объём j-ой группы

–частная средняя j-ой группы

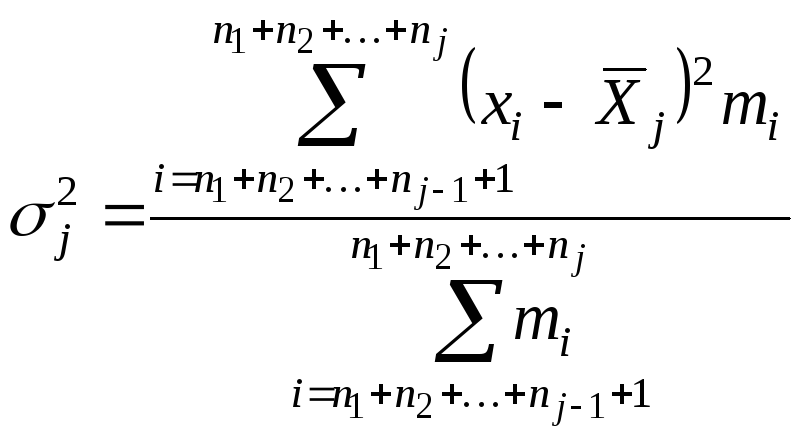(30)

Частные средние могут не совпадать с общей средней . Убедимся в этом:

n1 = 3	n2 = 5	n3 = 2
x1 x2 x3	x4 x5 x6 x7 x8	x9 x10
m1 m2 m3	m4 m5 m6 m7 m8	m9 m10

Разбили на три группы. l=3. Группы не пересекаются

n₁ + n₂ + … + n_l = k

n1, n2, n3 – число вариантов в группе	k = 10
	3 + 5 + 2 = 10

m₁ + m₂ + m₃ = N₁ – объём 1^ой группы (сумма частот в 1^ой группе)

m₄ + m₅ + … + m₈ = N₂ – объём 2^ой группы

m₉ + m₁₀ = N₃ – объём 3^ей группы

N_j – объём j^той группы

j = 1, 2, … , l

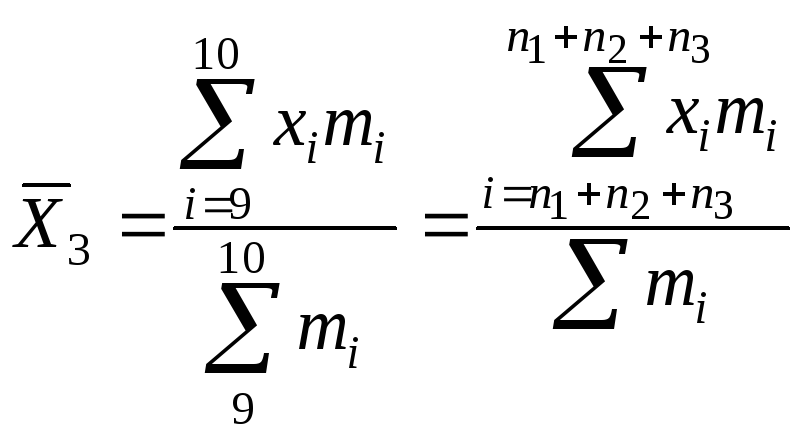
или

i = 3 + 5 + 1 = 8 + 1 = 9

Итак

,

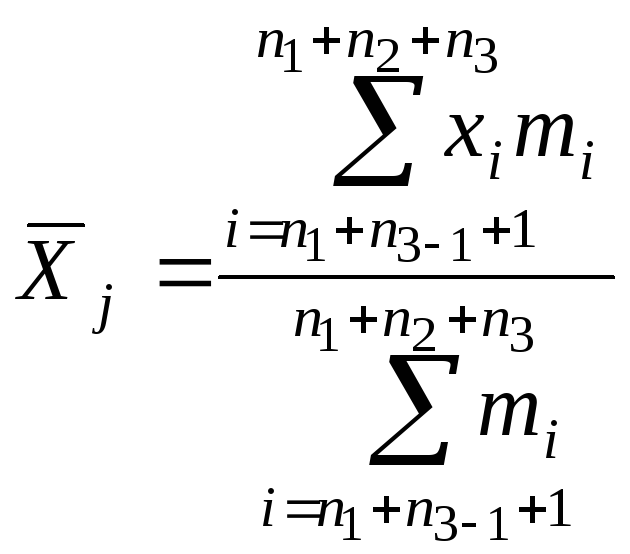где j = 1, 2, …, l

Отсюда видно, как получается формула (29).