флешка-все -документы / Ргр-

МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

УКРАЇНСЬКА ДЕРЖАВНА АКАДЕМІЯ ЗАЛІЗНИЧНОГО ТРАНСПОРТУ

ФАКУЛЬТЕТ «ЕКОНОМІКИ ТРАНСПОРТУ»

КАФЕДРА «ФІНАНСИ»

Розрахункова робота №

з дисципліни «ЕКОНОМЕТРИКА»

Варіант №-91

На тему: « »

Виконав студент гр.8-III-ЕП

Стратиенко В. О.

Перевірив:

(вчена ступінь, вчене звання

та П.І.Б викладача)

ХАРКІВ 2013

Використання метода експертних оцінок

Метод експертних оцінок-один з основних класів методів науково-технічного прогнозування, який ґрунтується на припущенні, що на основі думок експертів можна збудувати адекватну модель майбутнього розвитку об'єкта прогнозування.

Відправною інформацією при цьому є думка спеціалістів, які займаються дослідженнями й розробками в прогнозованій галузі.

Обробка результатів експертного дослідження з використанням ПЕОМ.

Мета: закріплення теоретичних знань та отримання практичних навичок щодо використання ПЕОМ з метою обробки результатів експертного дослідження.

Завдання

Треба проранжирувати чинники,тобто розташувати їх в порядку зменшення сили їх впливу на значення показника " які впливають на якість пасажирських перевезень ".

Експертам пропонується проранжирувати такі чинники :

х₁ - кількість рейсів на добу за маршрутом

х₂ - перегляд відеофільмів протягом шляху

х₃-додаткове платне обслуговування

х₄-додаткове безкоштовне обслуговування пасажирів

х₅-термін перебування пасажирів у дорозі

Порядок проведення експертизи:

1. Постановка задачі або експертизи;

2. Вибір експертів із числа осіб, компетентних у досліджуваній галузі.

3. Ранжирування чинників експертами;

4. Обробка інформації експертами;

5. Перевірка узгодженості і вірогідності експертних оцінок;

6. Використання результатів дослідження.

Суть експертної процедурі полягає в тому, що якомога більший кількості експертів пропонується оцінити вплив кожного з економічних чинників на досліджуваний економічний показник шляхом розташування чинників у порядку убування ступеня впливу. при цьому мінімальна кількість експертів дорівнює кількості ранжуємих чинників +2. Як правило, найбільш впливовому чиннику присвоюється ранг 1 і далі, по мірі впливу,- ранги 2,3,4 і т.п.

Таблиця 1 - Результати опитування експертів

Чинники	Ранги, які присвоєні чинникам експертами
	першим	другим	Третім	четвертим	п’ятим	шостим	сьомим
Х1	2	1	1	2	1	1	2
Х2	3	4	3	3	4	3	5
Х3	1	1	1	2	2	2	3
Х4	4	5	4	3	5	4	5
Х5	3	2	2	1	3	1	1

При ранжируванні деякі чинники можуть отримати однаковий ранг, тому додатковий ранг, тому додатково для таких чинників експерту пропонують за результатами повторної експертизи уточнити місця, які одержали чинники при загальному упорядкуванні всіх чинників у порядку убування рангів, тобто у порядку зменшення ступеня їх впливу на залежну змінну. В залежності від рангу і місця, які вони займають, чинники будуть мати ту чи іншу вагу. В розрахунку приймається, що вага місця дорівнює його номеру, але для чинників що мають однаковий ранг, вага дорівнює середній арифметичній вазі відповідних місць.

Таблиця 2 - Результати обробки експертних оцінок

Чинники	Експерти																													Підсумкова вага			Відхилення суми від середнього значення			Квадрати відхилень
	1				2				3				4				5				6				7
	ранг	місце	вага	ранг		місце	Вага	ранг		місце	вага	ранг		місце	вага	ранг		місце	вага	ранг		місце	вага	ранг		місце	вага
Х1	2	2	2	1		1	1,5	1		1	1,5	2		1	1,5	1		1	1,5	1		1	1,5	2		2	2	11,5			-9,5			90,25
Х2	3	3	3,5	4		4	4	3		4	4	3		3	3,5	4		4	4	3		4	4	5		4	4,5	27,5			6,5			42,25
Х3	1	1	1	1		2	1,5	1		2	1,5	2		2	1,5	2		2	1,5	2		3	3	3		3	3	13			-8			64
Х4	4	5	5	5		5	5	4		5	5	5		5	5	5		5	5	4		5	5	5		5	4,5	34,5			13,5			182,5
Х5	3	4	3,5	2		3	3	2		3	3	3		4	3,5	3		3	3	1		2	1,5	1		1	1	18,5			2,5			6,25
Разом			15				15				15				15				15				15				15	105			0			385

х_ср=

Для перевірки узгодженості думок експертів визначається коефіцієнт конкордації.

W=

де S- сума квадратів відхилень;

m- кількість експертів;

n-кількість чинників;

T_j-показник, що враховує збіг рангів і розраховується за формулою

,

де - число повторень k при ранжируванні чинників j-м експертом.

Якщо збігу рангів не було, то =1 та .

Коефіцієнт конкордації змінюється в межах 0≤W≤1.

Узгодженість вважається задовільною, якщо W≥0,5, якщо ж W≥0,7 , то узгодженість вважається хорошою. При повному збігу думок експертів W=1.

Для даного прикладу:

;

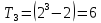
2³

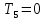
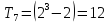
Отже W=

Вірогідність коефіцієнта конкордації перевіряється за критерієм Пірсона, розрахуємо значення якого визначається за формулою:

,

;

Розрахункове значення 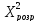порівнюється з табличним

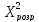
При заданих рівні значущості і числі ступенів свободи ᵧ=n-1,

де n -ількість чинників, обираємо табличне значення критерію Пірсона.

При 5% відхиленні p=0,95 кількість чинників y=5-1=4 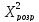більше - 23,16≥9,49 то гіпотеза про узгодженість думок 7 експертів при ранжуванні 5 чинників приймається.

Для вилучення найбільш впливових чинників будується діаграма убування впливу чинників (рис.1)

Ця діаграма будується по стовпцю «Підсумкова вага» таблиці 2.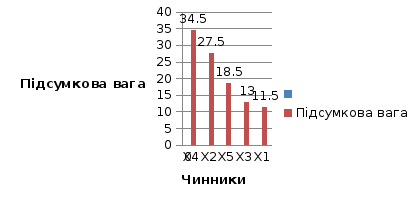

Рис.1- Визначення впливовості чинників

Проста вибіркова регресія

Прості парні лінійні регресійні моделі встановлюють лінійну залежність між двома змінними. При цьому одна із змінних вважається залежною (y), тобто ендогенною змінною та розглядається як функція незалежної змінної (x), тобто екзогенної.

У загальному вигляді проста вибіркова регресійна модель має вигляд:

y=a₀+a₁x+u,

де y -результативний показник (залежна змінна);

x - фактор (незалежна змінна);

a₀, a₁ -невідомі параметри регресійної моделі;

u - випадкова величина (помилкам або відхилення).

Регресійна модель називається лінійною, якщо вона лінійна за своїми параметрами. Її можна трактувати як пряму на площині, де а₀-перетин за віссю ординат, тобто параметр а₀ показує, чому дорівнює результативний показник, при значенні фактора 0, а a₁-це параметр, за значенням якого можливо оцінити наскільки зміниться результативний показник при збільшенні фактора на 1. При цьому за знаком параметру можливо визначити тип функції- пряма чи обернена. Так при додатному значенні a₁ можливо дістатися висновку, що при збільшенні фактору результативний показник токож збільшується, а при від'эмному значеннні цього параметра за умов збільшення незалежної змінної ендогенна змінна зменшується.

Розглянемо побудову простої лінійної регресійної моделі на конкретному прикладі залежності вартості оборотних активів і прибутку від діяльності підприємства залізничного транспорту.

Таблиця 3 - Вартості електроенергії та собівартості пасажирських перевезень .

Номер спостереження	1	2	3	4	5	6	7	8	9	10
Вартості електроенергії грн./пасс-км	1,2	1	0,6	0,9	0,6	0,8	0,7	1,1	0,6	0,9
Собівартість пасажирських перевезень грн./пасс-км	1,08	1,12	0,98	1,06	1,05	1,06	1,15	1,27	1,1	1,1

Аналіз даних показує , що збільшенням вартості електроенергії заробітна плати обслуговуючого персоналу зростає і затрати від собівартості пасажирських перевезень. Щоб виявити, на скільки підвищується в середньому собівартість пасажирських перевезень при збільшенні вартості електроенергії на 1 млн. грн., побудуємо модель y=a₀+a₁x+u, якщо припустити існування лінійного зв'язку між заробітною платою і собівартістю пасажирських перевезень, який виражається рівнянням прямої ỹ= a₀+a₁x.

Для оцінки параметрів побудуємо розрахункову таблицю.

Таблиця 4- Оцінка параметрів
Номер спостере-ження	Вартість електроенергії (хі),	Собівартість пасажирських перевезень
1	2	3	4	5	6
1	1,2	1,08	1,30	1,44	0,90
2	1,0	1,12	1,12	1,00	0,87
3	0,6	0,98	0,59	0,36	0,80
4	0,9	1,06	0,95	0,81	0,85
5	0,6	1,05	0,63	0,36	0,80
6	0,8	1,06	0,85	0,64	0,83
7	0,7	1,15	0,81	0,49	0,82
8	1,1	1,27	1,40	1,21	0,89
9	0,6	1,10	0,66	0,36	0,80
10	0,9	1,10	0,99	0,81	0,85
Разом	8,40	10,97	9,29	7,48	8,40

За даними розрахункової таблиці 7- отримаємо:

=, ; .

При цьому параметрі а₀ знаходится за формулою: .

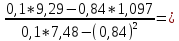= 0,1773

=0,84-0,1773*0,84=0,691

Рівняння прямої буде мати такий вигляд:

ỹ= 0,84+0,1489*х

Параметр а₁ - показує, що із збільшенням заробітної плати обслуговуючого персоналу на 1 грн. собівартість пасажирських перевезень збільшується в середньому на 0,0832 грн. Параметр а₀ - вільний член рівняння. Він характеризує значення ỹ при х=0, в нашому випадку ỹ=39,7696.

Підставимо значення незалежної змінної х в рівняння прямої ỹ= a₀+a₁x і знайдемо теоретичні значення результативного показника:

ỹ₁=0,84-0,1489*1,2=0,9

ỹ₂=0,84-0,1489*1,0=0,87

ỹ₃= 0,84-0,1489*0,6=0,8

ỹ₄=0,84-0,1489*0,9=0,85

ỹ₅=0,84-0,1489*0,6=0,8

ỹ₆=0,84-0,1489*0,8=0,83

ỹ₇=10,84-0,1489*0,7=0,82

ỹ₈=10,84-0,1489*1,1=0,89

ỹ₉=0,84-0,1489*0,6=0,8

ỹ₁₀=0,84-0,1489*0,9=0,85

Для використання коефіцієнта кореляції використовуємо розрахункову таблицю 5 .

Таблиця 5 -Розрахункова таблиця для визначення щільності зв'язку між вартістю електроенергії та заробітної плати обслуговуючого персоналу та собів артістю пасажирських перевезень.