флешка-все -документы / даша

Проста вибіркова регресія

Прості парні лінійні регресійні моделі встановлюють лінійну залежність між двома змінними. При цьому одна із змінних вважається залежною (y), тобто ендогенною змінною та розглядається як функція незалежної змінної (x), тобто екзогенної.

У загальному вигляді проста вибіркова регресійна модель має вигляд:

y=a₀+a₁x+u,

де y-результативний показник (залежна змінна);

x-фактор (незалежна змінна);

a₀, a₁-невідомі параметри регресійної моделі;

u - випадкова величина (помилкам або відхилення).

Регресійна модель називається лінійною, якщо вона лінійна за своїми параметрами. Її можна трактувати як пряму на площині, де а₀-перетин за віссю ординат, тобто параметр а₀показує, чому дорівнює результативний показник, при значенні фактора 0, а a₁-це параметр, за значенням якого можливо оцінити наскільки зміниться результативний показник при збільшенні фактора на 1. При цьому за знаком параметру можливо визначити тип функції- пряма чи обернена. Так при додатному значенні a₁можливо дістатися висновку, що при збільшенні фактору результативний показник токож збільшується, а привід'эмномузначеннні цього параметра за умов збільшення незалежної змінної ендогенна змінна зменшується.

Розглянемо побудову простої лінійної регресійної моделі на конкретному прикладі залежності вартості оборотних активів і прибутку від діяльності підприємства залізничного транспорту

Таблиця 6 - Заробітна плата обслуговуючого персоналу від собівартості пасажирських перевезень.

Номер спостереження	1	2	3	4	5	6	7	8	9	10
Заробітна плата обслуговуючого персоналу грн./пасс-км	29	19	18	18	29	32	23	33	16	22
Собівартістьпасажирських перевезень грн./пасс-км	2,96	2,57	2,4	2,51	3,52	3,3	2,49	3,53	1,71	2,4

Аналіз даних показує , що зі заробітної плати обслуговуючого персоналу зростає і прибуток від собівартості пасажирських перевезень. Щоб виявити, на скільки підвищується в середньому собівартість пасажирських перевезень при збільшенні заробітної плати обслуговуючого персоналу на 1 млн. грн., побудуємо модель y=a₀+a₁x+u, якщо припустити існування лінійного зв'язку між заробітною платоюі собівартістю пасажирських перевезень, який виражається рівнянням прямої ỹ= a₀+a₁x.

Для оцінки параметрів побудуємо розрахункову таблицю.

Таблиця 7-Оцінка параметрів

Номер спостере-ження	заробітна плата обслуговуючогог персоналу (хі),	собівартістьпасажирскихперевезень (уі), грн
1	2	3	4	5	6
1	29	2,96	85,84	841	4,40128
2	19	2,57	48,83	361	3,56928
3	18	2,4	43,2	324	3,48608
4	18	2,51	45,18	324	3,48608
5	29	3,52	102,08	841	4,40128
6	32	3,3	105,6	1024	4,65088
7	23	2,49	57,27	529	3,90208
8	33	3,53	116,49	1089	4,73408
9	16	1,71	27,36	256	3,31968
10	22	2,4	52,8	484	3,81888
∑	239	27,39	684,65	6073	39,7696

За даними розрахункової таблиці 7- отримаємо:

=, ; .

При цьому параметрі а₀знаходитсяза формулою: .

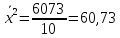
=0,0832

=2,739-0,0832*23,9=2,739-1,98848=1,98848

Рівняння прямої буде мати такий вигляд:

ỹ= 1,98848*0,0832*х

Параметр а₁ - показує, що із збільшенням заробітної плати обслуговуючого персоналу на 1 грн. собівартість пасажирських перевезень збільшуєтьсяв середньому на 0,0832 грн. Параметр а₀- вільний член рівняння. Він характеризує значення ỹ при х=0, в нашому випадкуỹ=39,7696.

Підставимо значення незалежної змінної х в рівняння прямої ỹ= a₀+a₁xі знайдемо теоретичні значення результативного показника:

ỹ₁=1,98848+0,0832*23,9=4,04128

ỹ₂=1,98848+0,0832*19=3,56928

ỹ₃=1,98848+0,0832*18=3,48608

ỹ₄=1,98848+0,0832*18=3,48608

ỹ₅=1,98848+0,0832*29=4,40128

ỹ₆=1,98848+0,0832*32=4,65088

ỹ₇=1,98848+0,0832*23=3,90208

ỹ₈=1,98848+0,0832*33=4,73408

ỹ₉=1,98848+0,0832*16=3,31968

ỹ₁₀=1,98848+0,0832*22=3,8188

Для використання коефіцієнта кореляції використовуємо розрахункову таблицю 8.

Таблиця 8-Розрахункова таблиця для визначення щільності зв'язку між заробітною платою обслуговуючого персоналу та собівартістю пасажирських перевезень.

№ спостереження	Заробітна плата виробн. персоналу (хі),	Собівартість пасажирскіх перевезень (уі),
1	2	3	4	5	6	7	8	9	10	11
1	29	2,96	4,40128	5,1	26,01	0,221	0,048841	1,1271	-1,44128	2,077288038
2	19	2,57	3,56928	-4,9	24,01	-0,169	0,028561	0,8281	-0,99928	0,998560518
3	18	2,4	3,48608	-5,9	34,81	-0,339	0,114921	2,0001	-1,08608	1,179569766
4	18	2,51	3,48608	-5,9	34,81	-0,229	0,052441	1,3511	-0,97608	0,952732166
5	29	3,52	4,40128	5,1	26,01	0,781	0,609961	3,9831	-0,88128	0,776654438
6	32	3,3	4,65088	8,1	65,61	0,561	0,314721	4,5441	-1,35088	1,824876774
7	23	2,49	3,90208	-0,9	0,81	-0,249	0,062001	0,2241	-1,41208	1,993969926
8	33	3,53	4,73408	9,1	82,81	0,791	0,625681	7,1981	-1,20408	1,449808646
9	16	1,71	3,31968	-7,9	62,41	-1,029	1,058841	8,1291	-1,60968	2,591069702
10	22	2,4	3,81888	-1,9	3,61	-0,339	0,114921	0,6441	-1,41888	2,013220454
∑	239	27,39	39,7696	0,00	360,9	0,00	3,03089	30,03	-12,3796	15,85775043

Використовуючи результати розрахунків таблиці 8, визначаємо коефіцієнт кореляції.

Критерієм, що характеризується щільністю зв'язку між залежною змінноюy і незалежною х, тобто наскільки значимим є вплив змінної х на у, є коефіцієнт кореляції:

=.

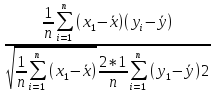Коефіцієнт кореляції є відносною мірою зв'язку між двома змінними. Значення коефіцієнта кореляції завждізнаяодится в межах

-1 та +1 (-1≤ ≤ +1). Додатне значення коефіцієнта кореляції свідчить про прямий, а від'ємне - про зворотній зв'язок між ними. Коли коефіцієнт кореляції прямує за абсолютною величиною до 1, то це свідчить що щільність зв'язку велика. В протилежному випадку, коли коефіцієнт кореляції прямує до 0 зв'язок слабкий, або зовсім відсутній.

Знаки параметра а₁та коефіцієнт кореляції повинні збігатися.

=.

За значенням коефіцієнту кореляції можливо дістатися висновку, що зв'язок між заробітною платою обслуговуючого персоналу і собівартості перевозок достатньо сильний, тобто зміна незалежної змінної тягне достатньо різку зміну екзогенної змінної. Також можна за знаком коефіцієнта кореляції видно, що при збільшенні ендогенної змінної збільшується і значення залежної змінної, тобто існує прямий зв'язок між досліджуваними показниками.

Наступним етапом проведення економетричного аналізу є підтвердження або спростування первинної гіпотези щодо лінійності зв'язку між обраними змінними. Для цього використовується коефіцієнт детермінації, який позначається 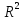.Коефіцієнт детермінації використовується як критерій адекватності моделі.

Коефіцієнт детермінації завжди додатній і знаходиться в межах від нуля до одиниці. коефіцієнт детермінації дорівнює квадрату коефіцієнта кореляції:

.

За допомогою коефіцієнта детермінації можна перевірити адекватність простої регресивної моделі. Якщо його значення близьке до одиниці, то можна вважати модель адекватна. Якщо його значення близьке до нуля, то модель адекватна. Якщо його значення близьке до нуля, то модель неадекватна, тобто немає лінійного зв'язку між змінними.

0 ≤ ˂0,45 - модель неадекватна тобто не існує лінійного зв'язку між змінними;

0,55 ˂≤ 1 - модель адекватна тобто існує лінійний зв'язок між змінними;

0,45 ≤ ≤ 0,55 - невизнаний коефіцієнт детермінації, тобто за його значенням неможливо визначити адекватність моделі.

Необхідно підтвердити, або скасувати у нашому випадку первинну гіпотезу щодо існування лінійного зв'язку між змінними. Для цього необхідно розрахувати коефіцієнт детермінації:

0,8242.

тобтодійсно існує лінійний зв'язок між заробітною платою обслуговуючого персоналу та собівартістю пасажирських перевезень.

У таких випадках необхідно використовувати інші показники. Отже, потрібен інший критерій, який би однозначно давав би відповідь на запитання про адекватність побудованої моделі. Найбільш поширеним з таких критеріїв е критерій Фішера.

Перевірка моделі заF- критерієм Фішера складається з певних етапів :

1. На першому етапі розрахуємо величину так званого F-відношення. (розрахункове значення):

F_(k-1,n-k)=

де n - кількість спостережень;

k- кількість параметрів моделі ( для простої регресії k=2).

2. На другому етапі задаємо рівень значущості .

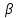3. На третьому етапі за статистичними таблицями F-розподілуФішера із(,)ступенями свободи та рівнем значущості , знаходимо критичне значення (Таблиця 9- с даними критичних значень).

4. Якщо розрахункове значення F ˃ F_кр, то можливо зробити висновок, що побудована регресійна модель адекватна, тобто дійсно існує лінійний зв'язок між х та у. ЯкщоF˂F_кр, то модель не адекватна, тобто зв'язок між досліджуваними змінними не лінійного виду.

Таблиця 9-Критичне значення F- критерію

К2	К1
	1	2	3	4	5	6	7	8	9
4	7,71	6,94	6,59	6,39	6,26	6,16	6,09	6,04	6,00
5	6,61	5,79	5,41	5,19	5,05	4,95	4,88	4,82	4,77
6	5,99	5,14	4,76	4,53	4,39	4,28	4,21	4,15	4,1
7	5,59	4,74	4,35	4,12	3,97	3,87	3,79	3,73	3,68
8	5,32	4,46	4,07	3,84	3,69	3,58	3,5	3,44	3,39
9	5,12	4,26	3,86	3,63	3,48	3,37	3,25	3,23	3,18
10	4,96	4,1	3,71	3,48	3,33	3,22	3,14	3,07	3,02

Для перевірки моделі на адекватність в даному прикладі визначимо насамперед число ступенів свободи. Зв'язок між заробітною платою обслуговуючого персоналу та собівартістю пасажирських перевезень існує, та рівняння простої регресії має два параметри k=2 і число ступенів свободи дорівнює: ᵧ₁=2-1=1 і ᵧ₂=10-2=8.

F=

За таблицею критичних значень F-розподілуФішера (див. таблицю-9) визначаємо, що при зазначених ступенях свободи і рівні значущості

критичне значення F-критерію - F_1,8(0,05)=5,32, тобто критичне значення F= 5,32 критерію менше розрахункового. Отже, побудована модель адекватна дійсності, тобто дійсно існує лінійний зв'язок між заробітною платою обслуговуючого персоналу та собівартістю пасажирських перевозок.