1.6.5. Метод двох вузлів

Цей метод є окремим випадком методу вузлових потенціалів, при застосуванні останнього до кола з усього двома вузлами, яке досить часто зустрічається на практиці. При цьому шуканою величиною є напруга між вузлами.

Розглянемо застосування методу двох вузлів на прикладі кола, схема якого наведена на рис. 1.27. Якщо нас не цікавлять струми між вузлами

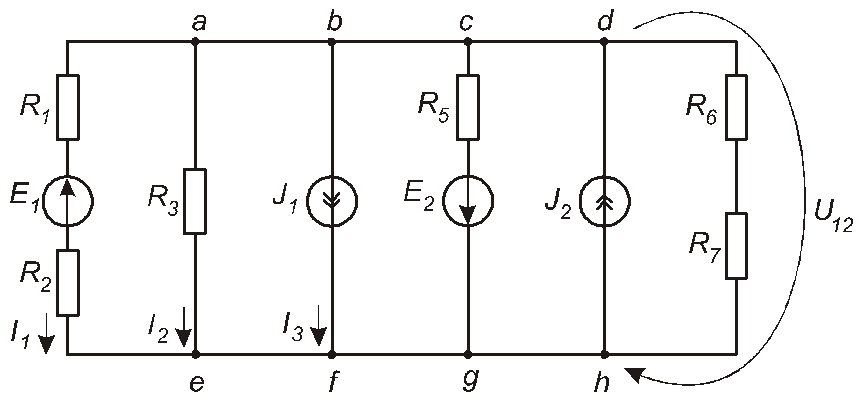
Рис. 1.27

атав,втас,стаd,етаf,fтаg,gтаhто можна, в думці, “стягти” вузлиa,b,c,d (які мають однаковий потенціал) в єдиний вузол 1. Аналогічно можна зробити з вузламиe, f, g, h,“стягуючи” їх до вузла 2 (рис. 1.28).

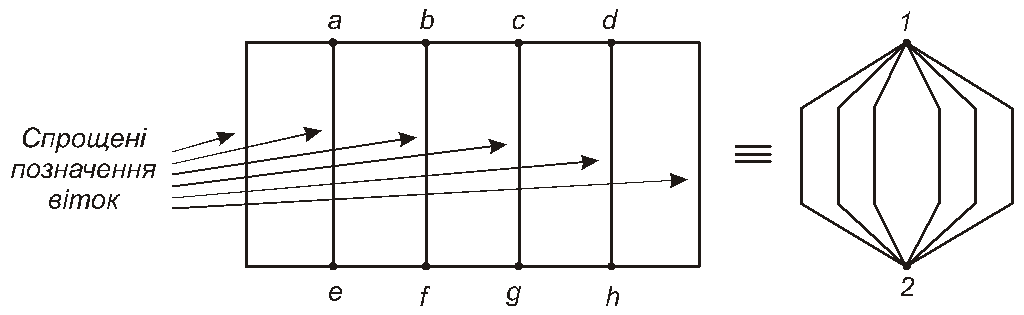
Рис. 2.28

Нехай відомі параметри всіх джерел та опори всіх резисторів.

Введемо провідності віток кола, пронумерувавши їх зліва направо:

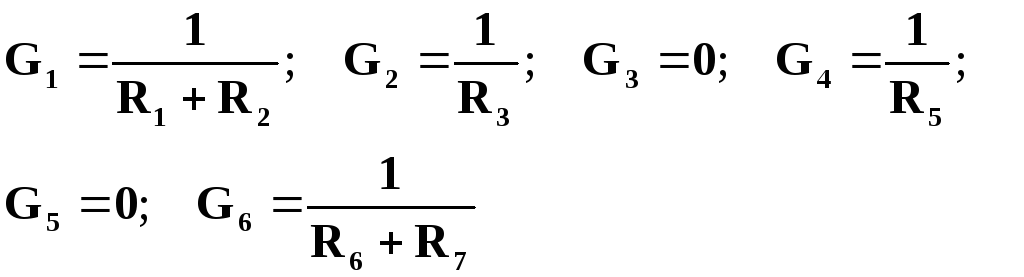
Зверніть увагу на те, що провідності віток з ідеальними джерелами струму обов’язково дорівнюють нулю.

Теоретично доведено (до речі, метод двох вузлів можна вивести не тільки з методу вузлових потенціалів – див. [1, 4]), що міжвузлова напруга дорівнює

Доданки в чисельнику існують тільки для тих віток, у яких є джерела, при цьому конкретний доданок береться із знаком “плюс”, якщо відповідне джерело спрямоване від вузла 2 до вузла 1, та із знаком “мінус” – у протилежному випадку.

У знаменнику знаходиться сума провідностей всіх віток кола.

Знаючи U₁₂, можна знайти струм у будь-якій вітці (крім віток з ідеальними джерелами струму, де струми й так відомі). Наприклад,I₂=U₁₂/R₃,аI₃=J₁. Для розрахунку струмуI₁використаємо закон Ома для вітки, яка містить резистор та ідеальне джерело напруги (рис. 1.13,б):

U₁₂=I₁(R₁+R₂)+E₁,

звідки I₁=(U₁₂-E₁)/(R₁+R₂).

Лекція 4

1.6.6. Еквівалентне перетворення з’єднання резисторів трикутником у з’єднання трипроменевою зіркою та обернене еквівалентне перетворення

У ряді випадків розрахунок кола можна значно спростити, якщо попередньо перетворити частину цього кола таким чином, щоб після перетворення залишилися незмінними напруги на затискачах перетвореної частини кола та струми в неперетвореній частині кола. Таке перетворення називається еквівалентним.

Розглянемо два кола. Перше з них утворюють резистори, з’єднані трикутником (рис. 1.29,а), а друге – резистори, з’єднані трипроменевою зіркою (рис. 1.29,б). Умови еквівалентної заміни одного з них на інше є такими:

I₁=I_1, I₂=I_2, I₃=I_3;

U₁₂=U_12, U₂₃=U_23, U₃₁=U_31.

Якщо відомі опори трикутника R₁₂, R₂₃, R₃₁, то опори еквівалентної зірки обчислюються так:

де R_ =R₁₂+R₂₃+R₃₁.

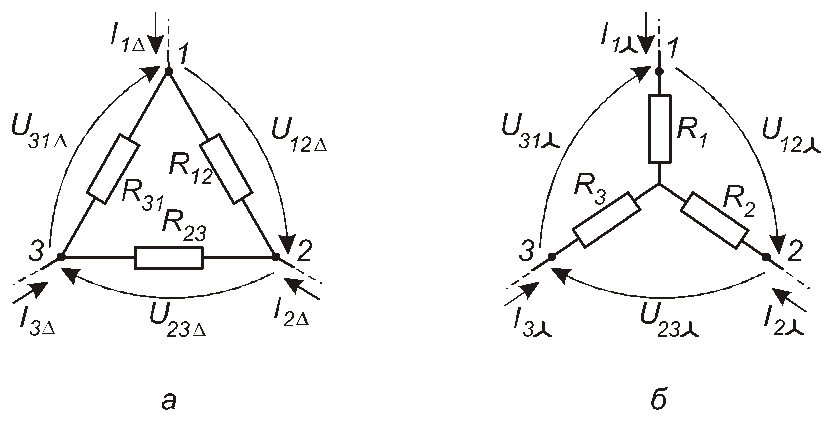
Рис. 1.29

Якщо відомі опори зірки R₁, R₂, R₃, то опори еквівалентного трикутника обчислюють так:

Випадок еквівалентного взаємного перетворення багатокутника в багатопроменеву зірку розглянутий у [2, 3].

1.7. Реальні джерела електричної енергії

1.7.1. Реальні джерела напруги та струму. Умови їх еквівалентності

Елементи будови, які утворюють шлях для протікання струму всередині будь-якого реального джерела, мають активний опір, більший за нуль. Цей опір (так заний внутрішній опір) має бути включений до кола, яке відтворює закономірність математичного зв’язку між напругою на затискачах модельованого джерела та струмом крізь ці затискачі, ідентичну аналогічній закономірності для реального джерела. Схему такого кола – “замінника” –називають схемою заміщення реального джерела.

Найпростіші схеми заміщення реального джерела напруги та реального джерела струму зображені відповідно на рис. 1.30,а та рис. 1.30,б. Тут R_Г– внутрішній опір джерела (генератора).

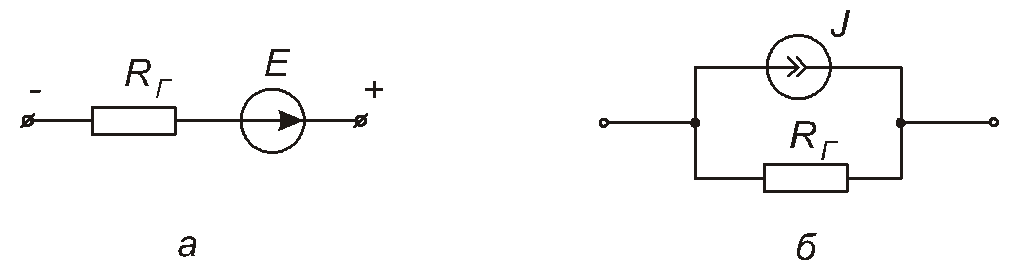
Рис. 1.30

Нехай до реального джерела напругипідключений резистор навантаженняR_н(рис. 1.31). Струм у навантаженні обчислюємо як

I=E/(R_Г+R_H),

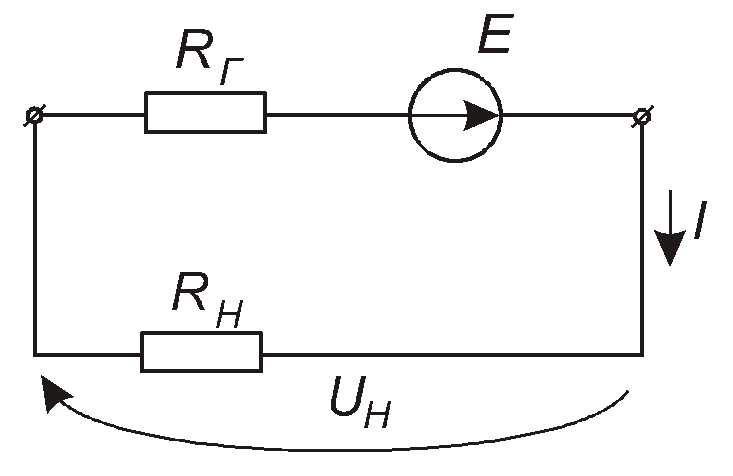
Рис. 1.31

звідки маємо напругу на навантаженні

Якщо R_Г R_H, тоU_H Eпри величинах струму від нуля до досить великих значень, тобтопри R_Г R_H реальне джерело напруги близьке до ідеального.

Зазначимо також, що напруга на затискачах реального джерела напруги за другим законом Кірхгофа дорівнює

U_H=E - IR_Г,

звідки випливає, що вона менша за ЕРС з причини падіння напруги на внутрішньому опорі джерелаR_Г.

Нехай до реального джерела струмупідключений опір навантаження R_Н(рис. 1.32). Нескладно довести, що струмIу навантаженні майже не залежатиме від опору навантаженняR_Н, якщоR_Н R_Г.

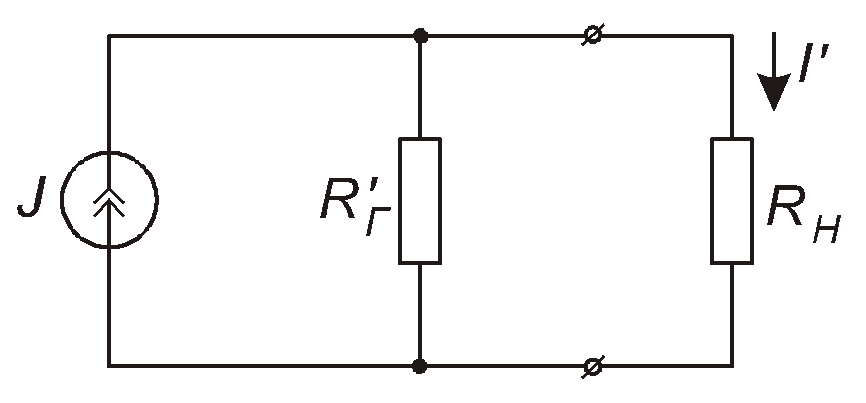
Рис. 1.32

За останньої умови реальне джерело струму близьке до ідеального.

А за яких умов реальне джерело напруги буде еквівалентним реальному джерелу струму? Тобто за яких умов струм Iу навантаженні (рис. 1.31) дорівнюватиме струмовіI(рис. 1.32), якщо опір навантаженняR_Нв обох випадках один і той самий?

Нескладно довести, що ці умови такі:

R_Г=R_Г, J=E/R_Г.