1.5.4. Розрахунок простого кола методом послідовних спрощень (згортання)

Розглянемо розрахунок струмів у елементах кола з мішаним з’єднанням елементів, але більш складного, аніж те, схема якого наведена на рис. 1.19. Нехай це буде коло, складене за схемою, зображеною на рис. 1.20. Припустимо, що відомими є величина ЕРС та величини опорів усіх резисторів Е=75В, R₁=5 Ом; R₂=15 Ом; R₃=R₅=30 Ом; R₄=20 Ом; R₆=60 Ом. Треба знайти струм у кожному резисторі.

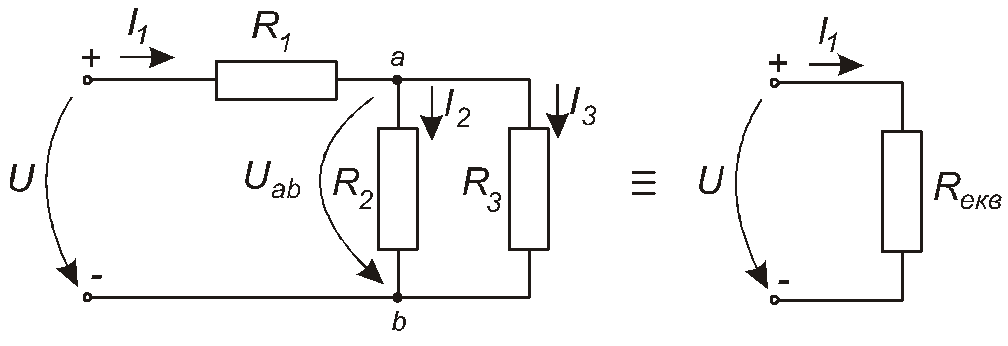
Рис. 1.20

Почнемо спрощувати (згортати) схему з її кінця. Резистори R₄, R₅, R₆з’єднані паралельно, тому замінюємо їх еквівалентним резисторомR₄₅₆, опір якого знаходимо за формулою (1.3) як

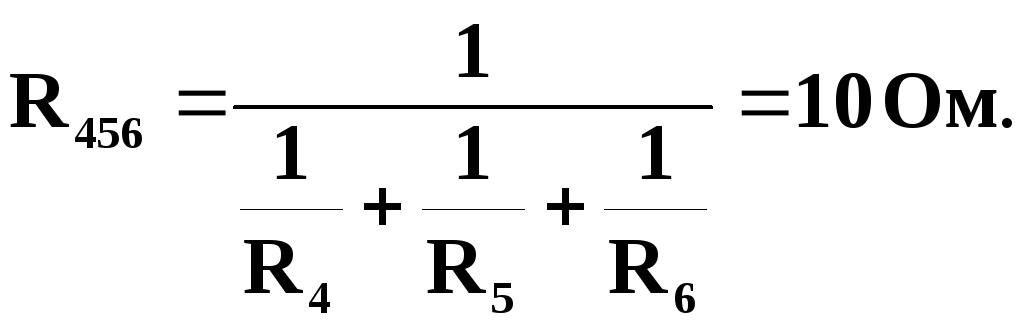
Резистори R₂таR₃також з’єднані паралельно, тому замінюємо їх еквівалентним резистором, опір якого знаходимо за формулою (1.3) або (1.4) (остання – зручніше) як

Зобразимо отриману спрощену схему (рис.1.21). Всі резистори тут

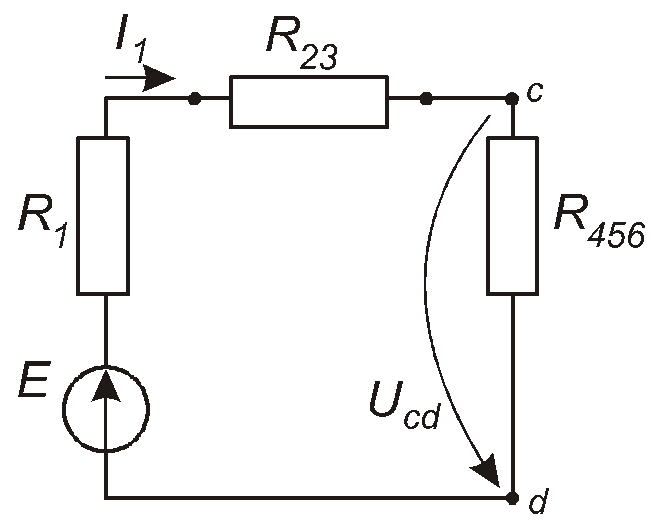
Рис. 1.21

з’єднані послідовно, тому одразу знаходимо

Далі знаходимо I₂таI₃за правилом розкиду:

(або за першим законом Кірхгофа, маємо I₃=I₁-I₂=1 A).

Щоб знайти I₄, I₅таI₆, треба знати напругуU_cd(рис. 1.20). Знаходимо її, користуючись спрощеною схемою (рис. 1.21), як

U_cd=I₁·R₄₅₆=30 B.

А тепер, згідно із законом Ома, знаходимо

Зауваження. Для розрахунку кіл з мішаним з’єднанням багатьох елементів знаходить застосування також метод пропорційних величин (див., наприклад, підручник [1]).

Лекція 3

1.6. Складні кола постійного струму

1.6.1. Загальні міркування з розрахунку складних кіл

Складне електричне коло – це таке коло, в якому хоча б частина елементів з’єднана так, що це з’єднання не є ані послідовним, ані паралельним. Прикладом такого кола є коло, схема якого наведена на рис. 1.22.

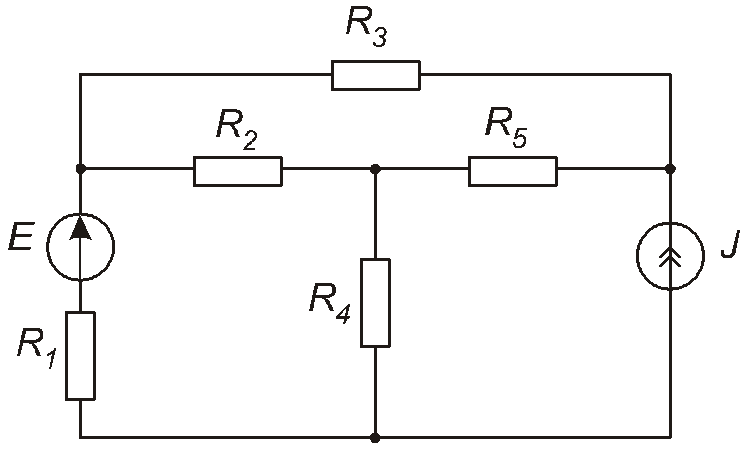
Рис. 1.22

Звичайно метою розрахунку кола є знаходження струмів у його вітках при відомих параметрах джерел та опорах резисторів. Тому кількість невідомих величин дорівнює кількості віток N_B. Тепер пригадаємо, що у вітці, яка містить ідеальне джерело струму, величина (сила) цього струму дорівнює силі струмуJцього джерела. Тому, якщо в колі є ідеальні джерела струму загальною кількістюN_Т, то кількість невідомих величин, шуканих при розрахунку, дорівнюватимеN_B – N_Т.

Отже, для однозначного знаходження величин струмів у всіх вітках складного кола слід попередньо скласти систему з (N_B – N_Т) рівнянь.

1.6.2. Метод рівнянь Кірхгофа

Цей метод полягає в складаннінеобхідної кількості рівнянь (див. попередній підрозділ) шляхом застосування обох законів Кірхгофа до розраховуваного колаі в подальшому розв’язанніодержаної системи рівнянь. Результатом розв’язання цієї системи будуть саме шукані струми у вітках. Це найбільш загальний метод розрахунку кола, але він потребує й найбільшої кількості обчислювальних операцій порівняно з іншими методами.

Розглянемо застосування методу рівнянь Кірхгофа на прикладі кола, схема якого наведена на рис.1.23. Відомими є Е₁, Е₂, J₁та опори всіх резисторів. Треба знайти струмиI₁, I₂, I₃, I₄, I₅.

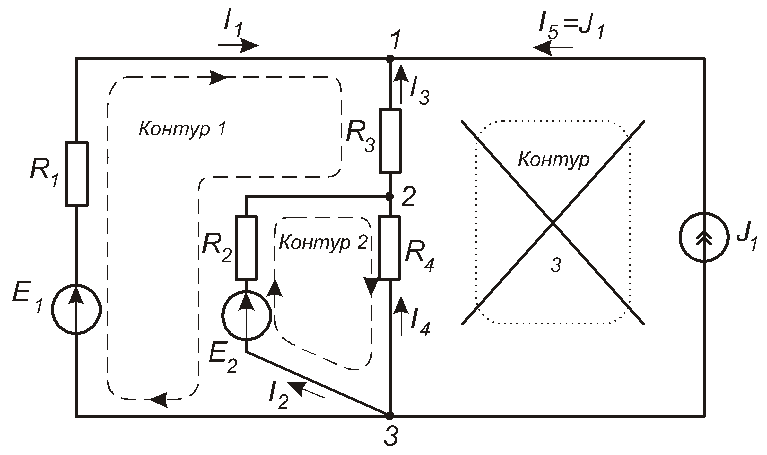
Рис. 1.23

1. Визначимо кількість віток N_B. Для цього колаN_B=5.

2. Задамося довільними напрямками струмів у вітках. Струм I₅має сенс спрямувати за напрямом струмуJ₁, бо вони все одно збігаються, як того вимагає дефініція ідеального джерела струму. Отже, кількість невідомих величин, а з нею – і потрібна кількість рівнянь складаютьN_B – N_Т = 5 – –1=4.

3. Визначимо кількість вузлів N_У(у даному випадкуN_У=3). Складемо рівняння за першим законом Кірхгофа для будь-яких (N_У –1) вузлів, наприклад для вузла 1 та вузла 2:

I₁+I₃+J₁=0, (1.5)

I₂+I₄=I₃. (1.6)

Важливе зауваження. Для останнього вузла (тут це вузол 3) рівняння за першим законом Кірхгофане складають, бо воно не є незалежним, а утворюється з лінійної комбінації рівнянь для перших (N_У –1)вузлів.

4. Визначимо кількість рівнянь, якої не вистачає для складання потрібної системи рівнянь. Всього треба скласти N_B – N_Т=4рівняння. Вже є(N_У –1) =2 рівняння. Тому треба щеN_B – N_Т –(N_У–1)=5–1–2рівняння.

Складемо їх на базі другого закону Кірхгофа. Спочатку оберемо контури та довільно оберемо напрямки їх обходів (див. рис. 1.23). При цьому обираємо тільки незалежні контури, тобто такі контури, кожен з яких містить хоча б одну вітку, яка не входить до іншого контуру. Тепер складемо рівняння для контуру 1 та контуру 2:

Е₁–Е₂=I₁R₁–I₃R₃–I₂R₂ (1.7)

Е₂=I₂R₂–I₄R₄. (1.8)

Важливе зауваження. Для контурів, які охоплюють ідеальні джерела струму, рівняння за другим законом Кірхгофане складають.Тому в даному випадку не складають такого рівняння для контуру 3.

5. Розв’язуємо систему чотирьох рівнянь (1.5) – (1.8) і знаходимо шукані струми I₁, I₂, I₃, I₄(струмI₅автоматично дорівнює струмуJ₁).

Увага!Якщо деякі із струмів виявляться від’ємними, це свідчитиме про те, що справжній напрямок протікання струму протилежний напрямку, який довільно обрано при виконанні п.2. Цей висновок справедливий для будь-якого методу розрахунку кіл.