1.4. Потужність, розсіювана резистором. Закон Джоуля-Ленца

Вивчаючи нагрівання дротів струмом, Джоуль та Ленц у 1844р. незалежно один від одного встановили, що теплова енергія A, яку виділяє струм силоюIв проводі з опоромRза часt, обчислюється як

(закон Джоуля-Ленца). Сучасною одиницею вимірювання в системі SI є Джоуль (Дж).

Як відомо з курсу фізики, потужність P дорівнюєA/t, тому із закону Джоуля-Ленца отримуємо величину потужності, розсіюваної резистором з опоромR, у вигляді

.

Враховуючи, що U=IR(закон Ома), можна отримати ще дві формули для обчислення потужності:

Замінивши вираз на провідністьG, отримаємо також, що

P=U²G.

1.5. Прості кола постійного струму

1.5.1. Коло з послідовним з’єднанням резисторів

Послідовним з’єднанням елементів (або ділянок кола) називають таке з’єднання, при якому крізь усі ці елементи (або ділянки кола) протікає один і той самий струм.

Схема кола, яке являє собою послідовне з’єднання Nрезисторів, наведена на рис. 1.16. Тут маємо

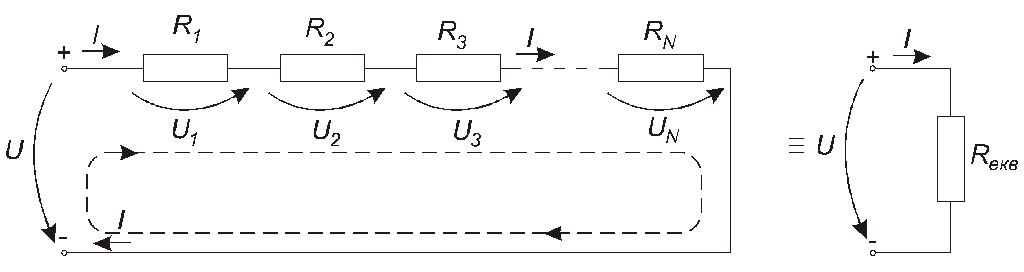
Рис.1.16

U₁=IR₁; U₂=IR₂; U₃=IR₃; ; U_N=IR_N.

За другим законом Кірхгофа

U=U₁+U₂+U₃+…+U_N=IR₁+IR₂+IR₃+….IR_N=

=I·(R₁+R₂+R₃+….+R_N) = I·R_екв.

З порівняння правої та лівої частин останньої рівності робимо висновок, що при послідовному з’єднанні Nрезисторів їх усіх можна замінити одним еквівалентним резистором, опір якого дорівнює

R_екв = R₁ + R₂ + R₃ +….+ R_N.

1.5.2. Коло з паралельним з’єднанням резисторів

Паралельним з’єднанням елементів (або ділянок кола) називають таке з’єднання, при якому всі ці елементи (або ділянки кола) знаходяться під однією і тією самою напругою.

Схема кола, яке являє собою паралельне з’єднання Nрезисторів, наведена на рис. 1.17,а. Таке з’єднання частіше зображують у вигляді схеми , наведеної на рис. 1.17,б.

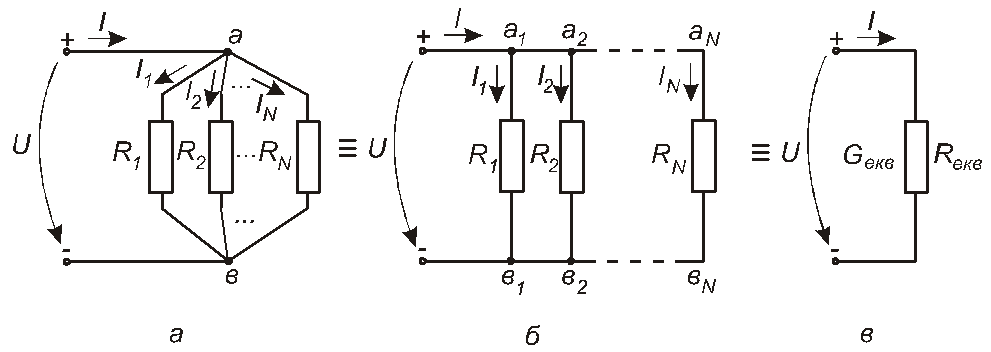
Рис. 1.17

Це друге коло є еквівалентним першому. Потенціали точок а₁,....,а_N колаб)дорівнюють потенціалам точкиаколаа); а потенціали точокв₁,.....,в_Nдорівнюють потенціалу точкив, так що всі резистори знаходяться під однаковою напругоюU. Тоді маємо

За першим законом Кірхгофа

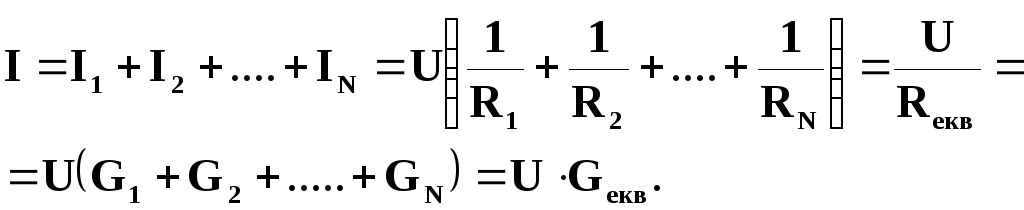
Отже, еквівалентним опором N паралельно з’єднаних резисторів буде

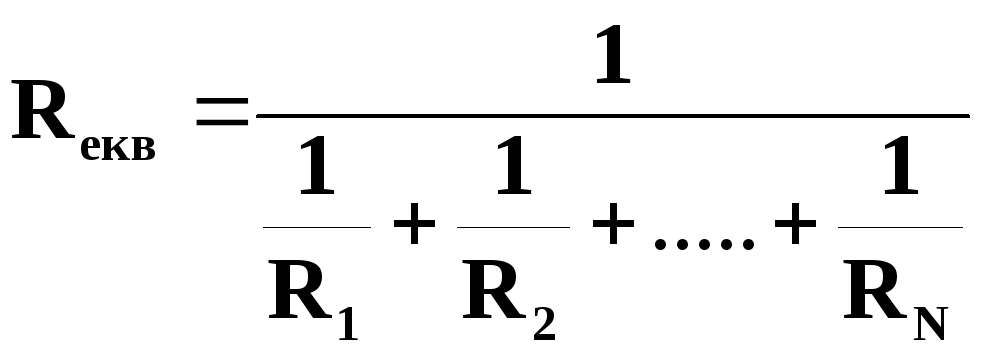, (1.3)

а їх еквівалентною провідністю буде

G_екв= G₁+G₂+……+G_N.

Важливим для практики є випадок паралельного з’єднання двох резисторів (рис. 1.18). При цьому N=2, і з формули (1.3)

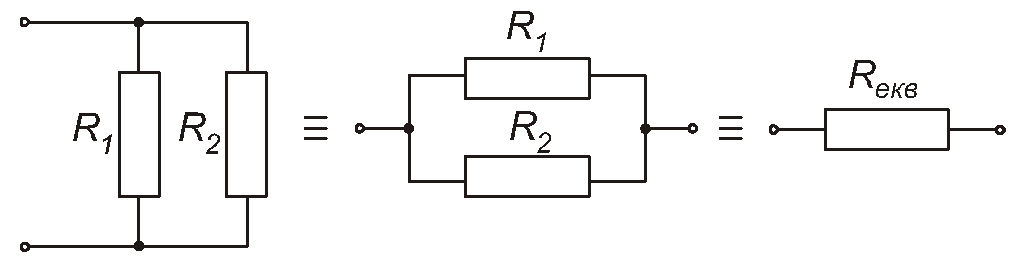
Рис. 1.18

отримуємо, що

. (1.4)

1.5.3. Коло з мішаним з’єднанням резисторів. Правило розкиду струмів

Мішане з’єднанняелементів (ділянки кола) – це таке з’єднання, при якому коло складається з послідовно та паралельно з’єднаних елементів (ділянок кола).

Схема кола, яке являє собою найпростіший варіант мішаного з’єднання елементів, наведена на рис. 1.19.

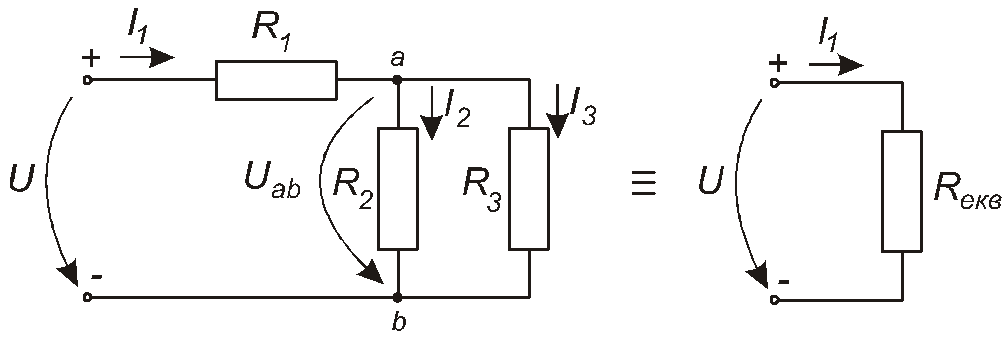
Рис. 1.19

Тут резистор R₁послідовно з’єднаний з ділянкоюав, яка являє собою паралельне з’єднання опорівR₂таR₃. Отже, еквівалентним опором є

.

Тоді маємо

I₁=U/_Rекв,

За законом Ома

.

Останні дві рівності називають правилом розкиду струмів. Його зручно використовувати, коли відомий струм, який втікає у два паралельно з’єднаних резистора з відомими опорами.