1.1.5. Пасивні елементи електричного кола постійного струму

Елементи кола, які не утворюють електричної енергії, є пасивними елементами. В переважній більшості випадків кола постійного струму містять пасивні елементи лише одного типу. Це резистори (активні опори) – такі елементи, основною властивістю яких є чинення опору протіканню постійного струму. Умовне позначення резистора подане на рис. 1.6.

Активним опором називають також числову величину опору, що резистор чинить протіканню струму.

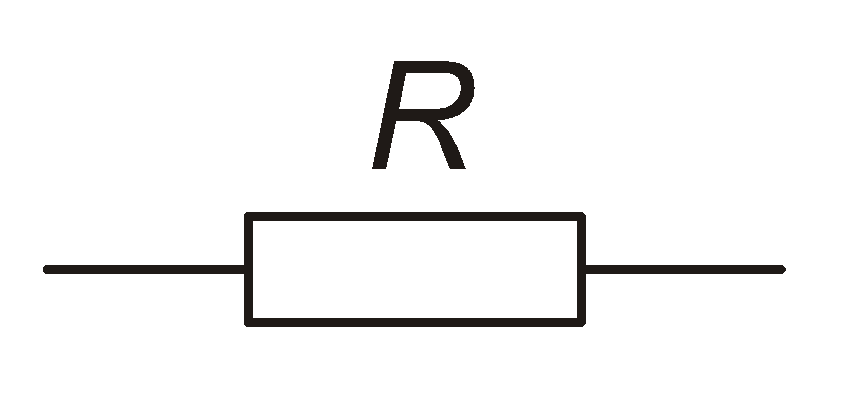
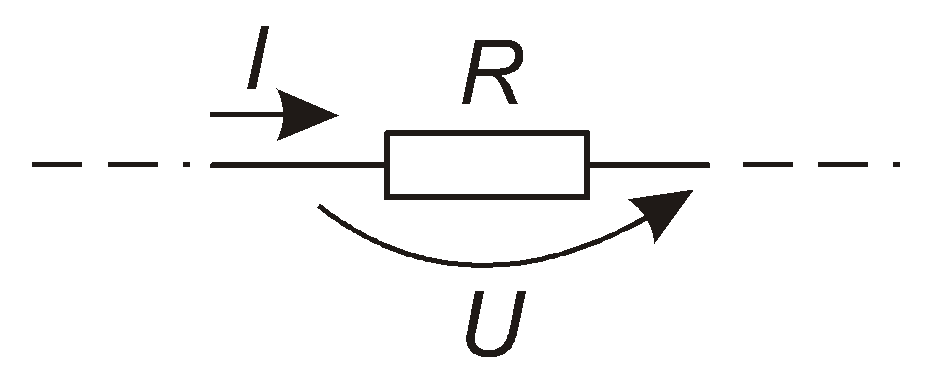
Рис. 1.6 Рис. 1.7

Ця величина Rдорівнює відношенню постійної напругиUна резисторі до струмуI, який при цьому протікає крізь цей резистор (рис. 1.7):

.

Іноді резистор характеризують його провідністю G– величиною, зворотною до опору:

Відомі з курсу фізики ідеальна котушка індуктивності Lта ідеальний конденсаторСу колах постійного струму являють собою відповідно провідник та розрив кола (рис. 1.8.).

Рис. 1.8

Якщо електричне коло складене з резисторів, ідеальних котушок індуктивності та ідеальних конденсаторів, параметри R,LтаСяких не залежать від числових значень та напрямів струмів у цих елементах, то таке коло називаютьлінійним електричним колом.

1.1.6. Топологічні елементи кола: вузол, вітка, контур

Вузол – це точка кола, в якій з’єднані затискачі трьох або більше елементів. Приклад наведено на рис. 1.9.

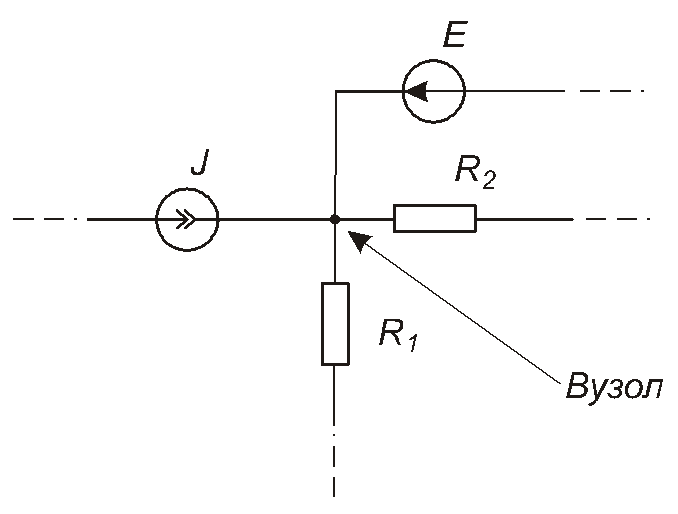
Рис. 1.9

Вітка– ділянка кола, розташована між двома вузлами, яка не містить інших вузлів. По ній протікає один і той самий струм. Приклад наведено на рис.1.10.

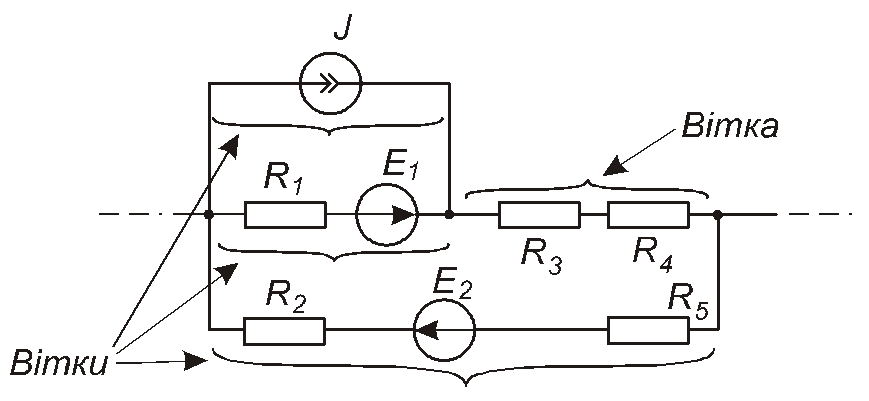
Рис. 1.10

Контур – замкнений шлях, який проходить по кільком віткам, при цьому кожний вузол зустрічається не більш ніж один раз. Тобто це – неперервна послідовність віток без повторів. Вибір напряму обходу – довільний. Приклад наведено на рис. 1.11, де контури позначені штриховими лініями.

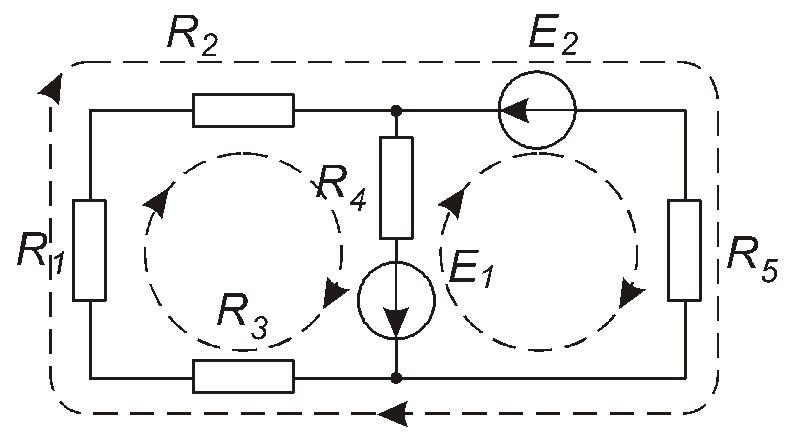
Рис. 1.11

Лекція 2

1.2. Закон Ома

В сучасному формулюванні закон Ома є таким: напруга між кінцями провідника прямо пропорційна опорові Rцього провідника та силіIструму крізь нього:

. (1.2)

При цьому вважається, що UтаIспрямовані однаково (рис.1.12,а). Якщо ж вони спрямовані в протилежні боки (наприклад, як на рис.1.12,б), то маємо

.

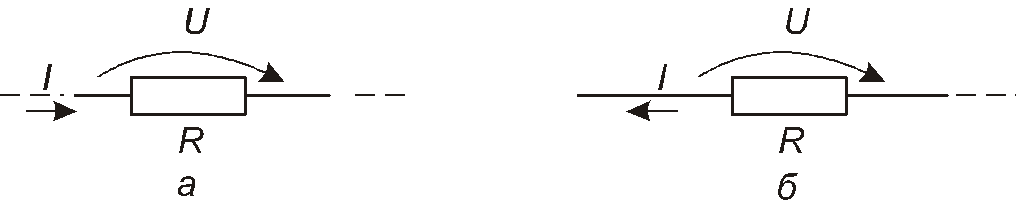
Рис.1.12

Закон Ома можна також поширити на випадок, в якому розглядається ділянка кола, яка містить послідовно з’єднані резистор та ідеальне джерело напруги. При цьому для випадку, показаного на рис. 1.13,а маємо

та

,

а для випадку, показаного на рис. 1.13,б, маємо

.

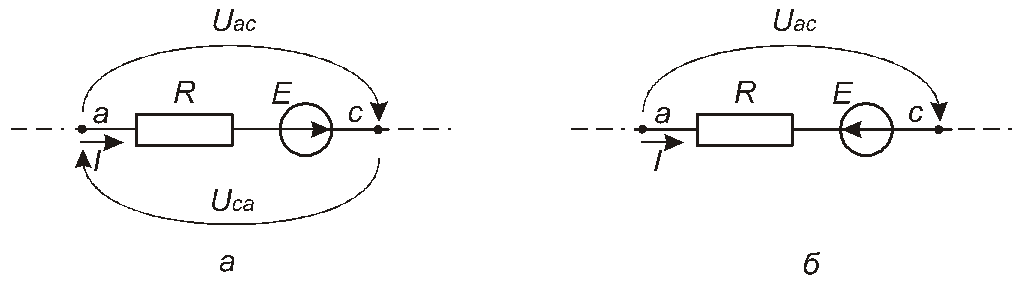
Рис. 1.13

1.3. Закони Кірхгофа

Перший закон Кірхгофа: алгебраїчна сума струмів віток, що сходяться в одному і тому ж вузлі, дорівнює нулю.

Звичайно прийнято струми, що втікають у вузол, включати до цієї суми із знаком “плюс”, а ті, що витікають – із знаком “мінус”. Тому в прикладі , показаному на рис. 1.14, отримаємо

,

або

.

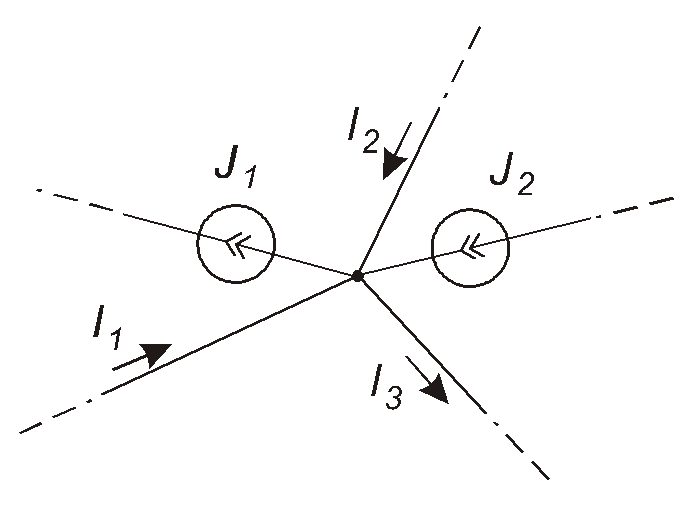
Рис. 1.14

Остання рівність ілюструє інше формулювання першого закону Кірхгофа:арифметична сума струмів, що втікають у вузол, дорівнює арифметичній сумі струмів, що витікають з нього.

Другий закон Кірхгофа: в замкнутому контурі алгебраїчна сума напруг дорівнює алгебраїчній сумі ЕРС.

Звичайно прийнято напруги та ЕРС, що збігаються з напрямом обходу контуру, включати до своїх сум із знаком “плюс”, а ті з них, що протилежні напряму обходу контуру, включати до своїх сум із знаком “мінус”. Тому в прикладі, показаному на рис. 1.15, отримаємо

,

або

,

де .

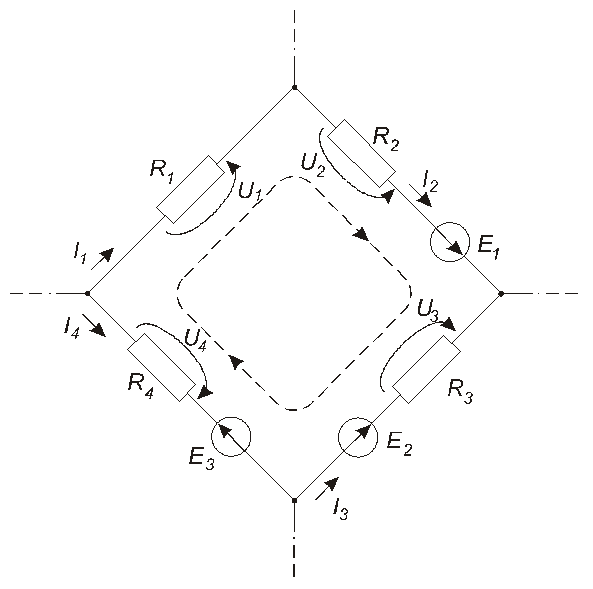
Рис. 1.15