4.8.2. Коло з паралельним з’єднанням комплексних опорів

Розглянемо коло, утворене шляхом паралельного з’єднання двополюсників з комплексними опорами Z₁, Z₂,...Z (рис.4.42,а), для кожного з яких справедлива примітка, зроблена в п.4.8.1.

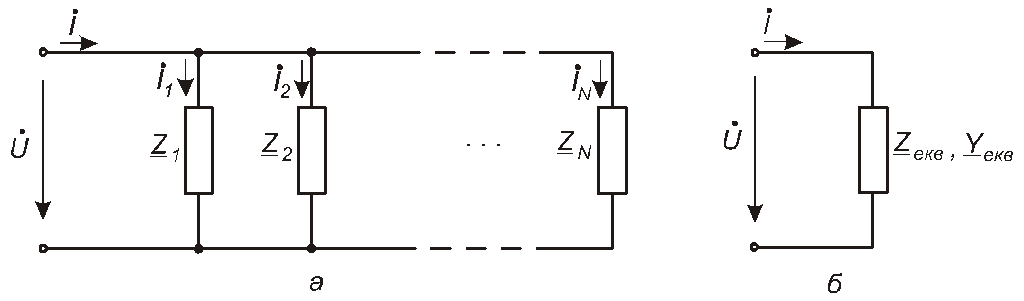
Рис. 4.42

Згідно з першим законом Кірхгофа маємо

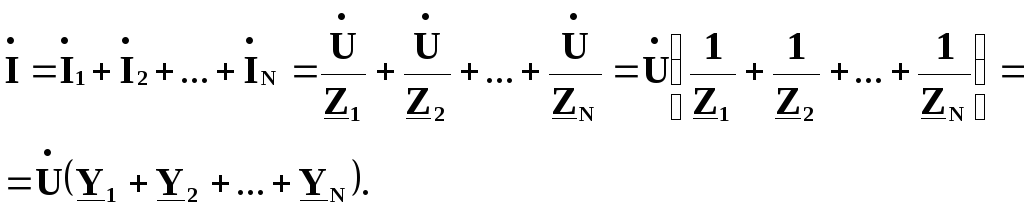
Опір Z_екв, еквівалентний опору цих паралельно з’єднаних двополюсників, знайдемо, порівнявши останній вираз та закон Ома, записаний для кола, схему якого зображено на рис. 4.42,б:

Одержуємо, що

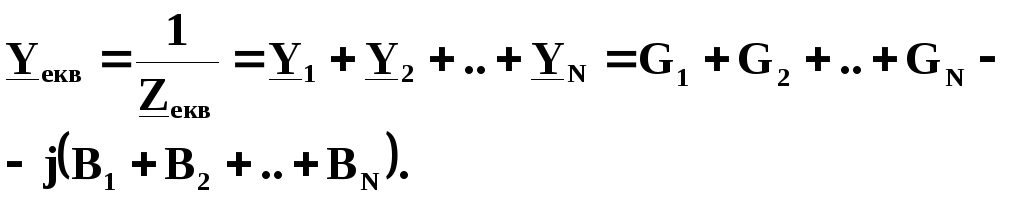
Звідки

.

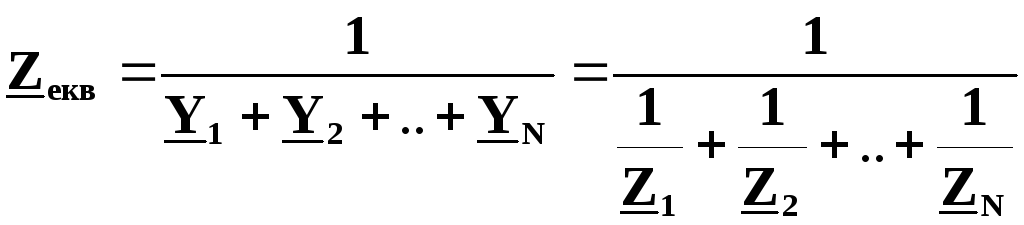Важливим окремим випадком є паралельне з’єднання двох комплексних опорів (рис. 4.43). Маємо:

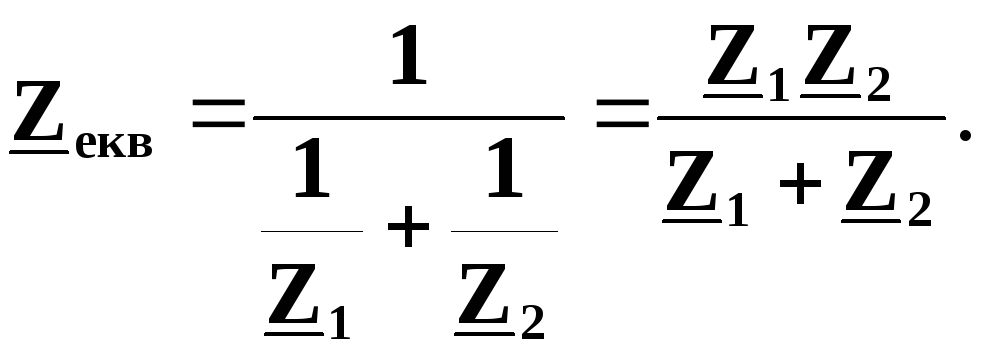
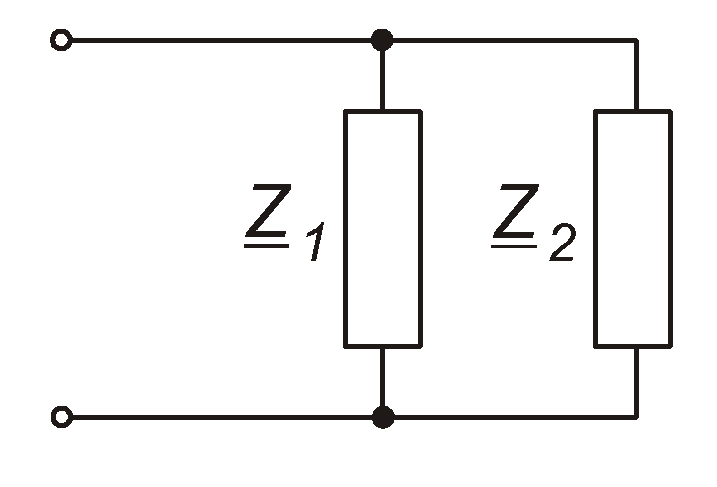
Рис. 4.43

Наприклад, при паралельному з’єднанні двох реальних котушок індуктивності (рис. 4.44) отримаємо

.

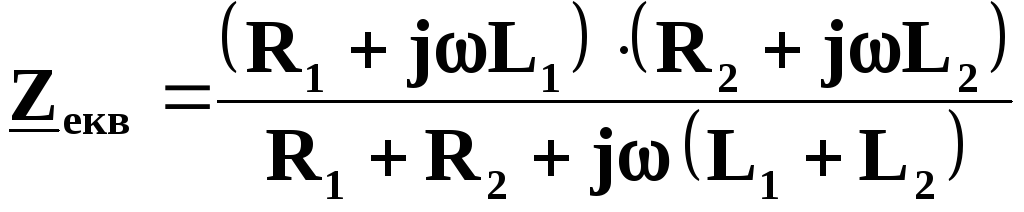Після підстановки числових даних, виконавши множення та ділення, переведемо отримане комплексне число до алгебраїчної форми і, таким чином, визначимо величини R_екв та Х_екв.

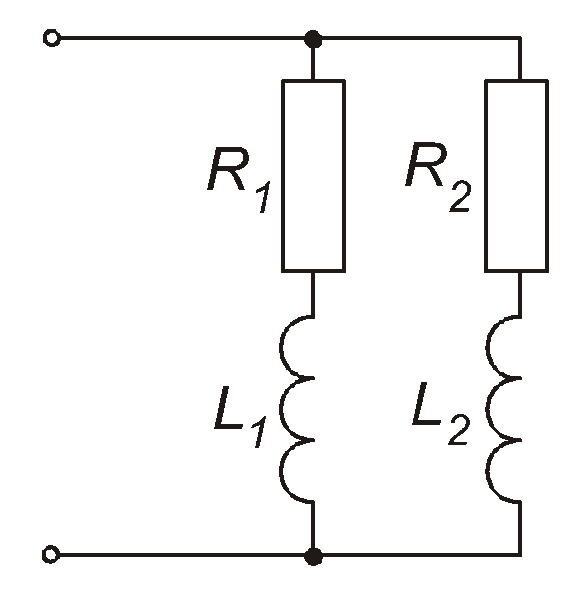
Рис. 4.44

4.8.3. Коло з мішаним з’єднанням комплексних опорів

Нагадаємо, що коло з мішаним з’єднанням елементів – це таке коло, яке утворене з ділянок, які містять тільки послідовно та паралельно з’єднані елементи. Схему найпростішого варіанта такого кола наведено на рис. 4.45. Опір паралельної ділянки ав цього кола дорівнює

,

а еквівалентний опір всього кола дорівнює

.

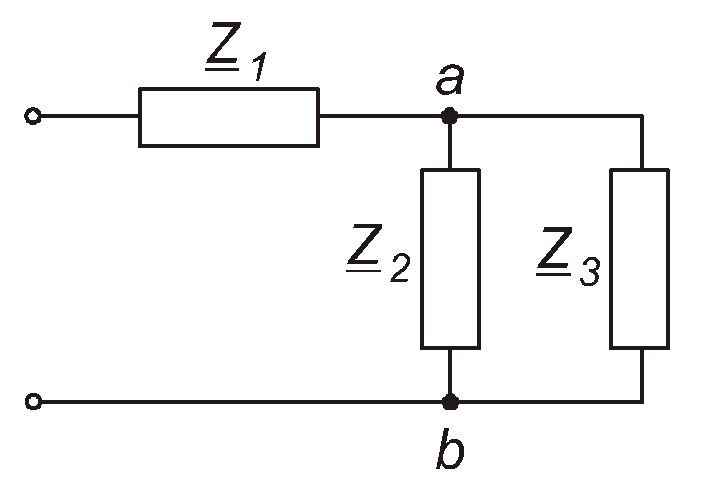
Рис. 4.45

4.9. Застосування методів розрахунку кіл постійного струму до розрахунку кіл синусоїдного струму

Усі методи розрахунку кіл постійного струму одержані на базі законів Ома та Кірхгофа. Але ж ці закони є справедливими й для кіл синусоїдного струму. Тому всі методи розрахунку кіл постійного струму придатні і для розрахунку кіл синусоїдного струму. Певні обмеження накладено тільки на розрахунок кіл з індуктивним зв’язком між елементами. Зауважимо також, що після виконання еквівалентного перетворення “зірки” на “трикутник” або після оберненого перетворення числові значення деяких активних опорів можуть бути від’ємними. Це не повинно турбувати розраховувача, оскільки ці перетворення мають проміжний характер, і в кінцевій схемі всі активні опори будуть невід’ємними.

Звичайно, що при розрахунку комплексним методом у формулах, отриманих для кіл постійного струму, слід використовувати тільки комплексні опори елементів і ділянок, а також комплекси діючих значень струмів, напруг і ЕРС (або відповідні комплексні амплітуди).

4.10. Умови передачі генератором максимуму активної потужності до комплексного навантаження

Розглянемо коло, утворене послідовним з’єднанням реального джерела синусоїдної напруги (комплекс діючого значення його ЕРС позначимо як , а комплексний внутрішній опір – як) та навантаження з комплексним опором(рис. 4.46). Нехай відомі величиниR_г та Х_г.

Треба визначити величини R_н та Х_н за умови, що активна потужність Р_н, споживана навантаженням, є максимальною.

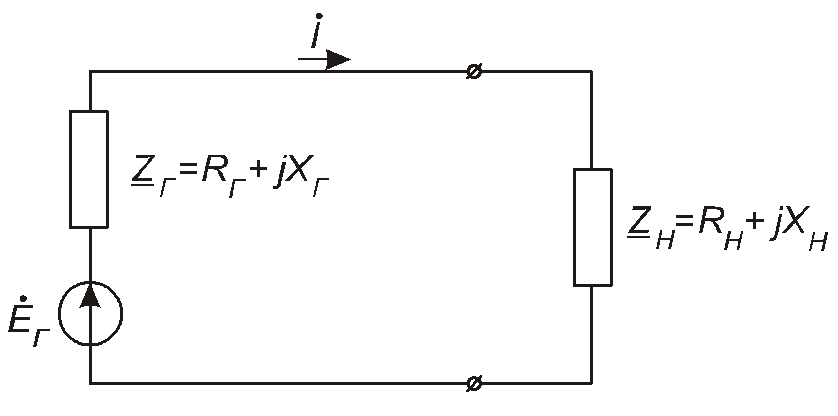
Рис. 4.46

Як показано в п. 4.7, величину активної потужності, споживаної навантаженням, можна знайти як Р_н=I²R_н. Тому попередньо знаходимо струм у нашому колі:

.

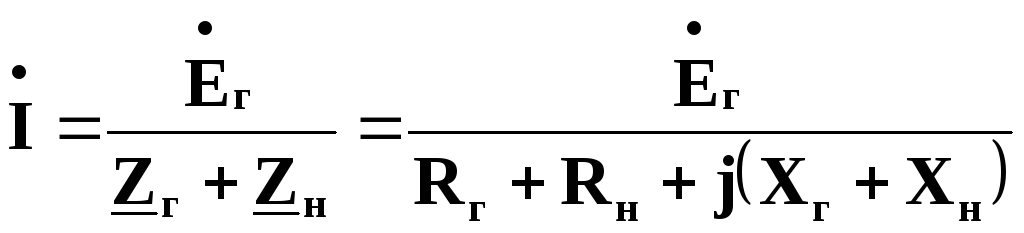Звідси

.

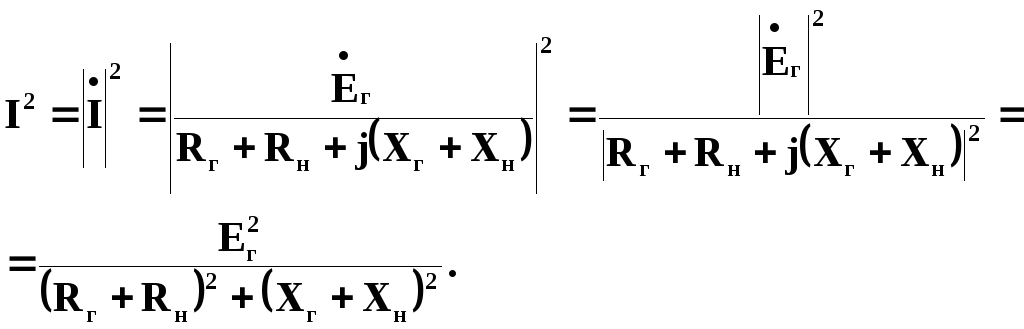Тоді

.

Щоб Р_н була максимальною, треба, щоб знаменник цього дробу був мінімальним. Очевидно, що за будь-яких додатних значень R_г та R_н потужність буде максимальною, якщо

Х_н = –Х_г. (4.42)

При цьому

.

Дослідивши на екстремум цю функцію величини R_н, отримаємо, що Р_н буде максимальною за умови

R_н=R_г. (4.43)

В термінах комплексних опорів результати (4.42) та (4.43) можна поєднати:

, (4.44)

де зірочка є символом операції комплексного спряження.

Навантаження, комплексний опір якого задовольняє співвідношенню (4.44), називають спряженим навантаженням. Воно споживає від генератора максимально можливу потужність, величина якої

.
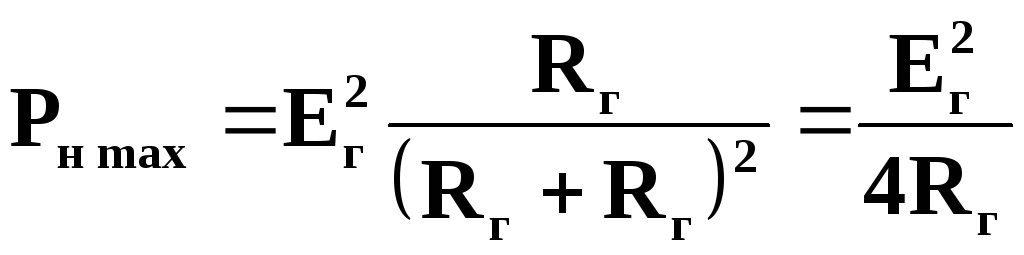