Лекція 18

4.7. Потужність у колах синусоїдного струму

Розглянемо деякий двополюсник з комплексним опором . Крізь нього протікає струм, який утворює на цьому двополюснику падіння напруги(рис. 4.39).

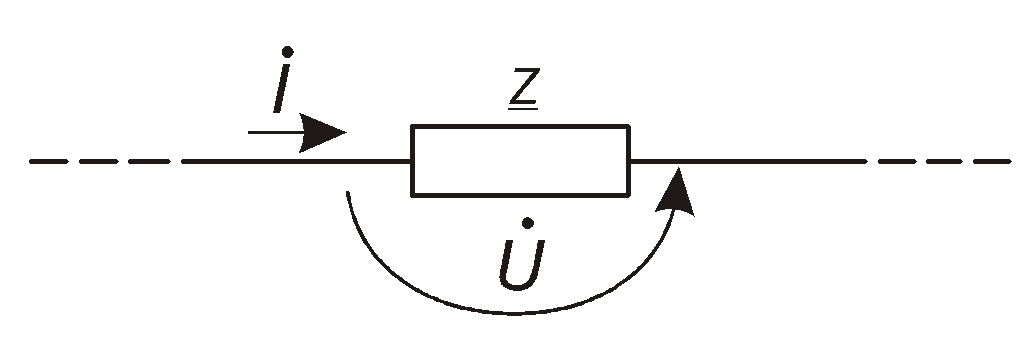
Рис. 4.39

Комплексна потужність визначається як добуток комплексу діючого значення напруги на спряжений комплекс діючого значення струму крізь двополюсник:

Але ж, як показано в підрозділі 4.6.3, величина _U-_I=, де  – аргумент комплексного опору кола . Тому

. (4.38)

Оскільки , то можна записати, що

, (4.39)

а також, що

, (4.40)

де “” – знак комплексного спряження.

Введемо поняття повної потужності S, споживаної колом: .

Порівнявши формули (4.38), (4.39) та (4.40), можна помітити, що

.

Як комплексну, так і повну потужності вимірюють у вольтах, помножених на ампер (скорочене позначення ВА).

Отже,

.

Тут єактивною потужністю. Вона безповоротно споживається колом. Одиниця вимірювання – ват (Вт). Ця потужність завжди більша за нуль або дорівнює нулю (якщо тільки не йдеться про коло з підсилювальними елементами: в ньому P може бути від’ємною).

Величина cos дістала назву “коефіцієнт потужності”, оскільки вона показує, яку частину повної потужності безповоротно споживає дане коло. Вона має велике значення в електропостачанні.

Величина єреактивною потужністю. Ця потужність то накопичується колом (в індуктивних і ємнісних елементах), то повертається до джерела. Одиницею вимірювання є вар (ВАр - від слів “вольт”, “ампер”, “реактивна”). Величина Q може бути як додатною, так і від’ємною.

Отже,

. (4.41)

Порівнявши цю рівність з рівністю (4.39), отримаємо:

.

Порівнявши (4.41) та (4.40), отримаємо:

.

Відклавши величину P на осі дійсних чисел, а величину Q – на осі уявних чисел комплексної площини, отримаємо трикутник потужностей (його заштриховано на рис. 4.40). Очевидно, що

.

Рис. 4.40

Комплексну потужність ідеального джерела синусоїдної напруги обчислюють за формулою

,

де – спряжений комплекс діючого значення струму, який протікає крізь це джерело. Знак обирають з тих же міркувань, з яких це роблять для кіл постійного струму (підрозділ 1.11).

Комплексну потужність ідеального джерела синусоїдного струму обчислюють за формулою

,

де – напруга на затискачах цього джерела. І тут знак також обирають з тих же міркувань, що й для кіл постійного струму (підрозділ 1.11).

Баланс потужностей для кола синусоїдного струму полягає в рівності алгебраїчної суми комплексних потужностей усіх джерел кола та алгебраїчної суми комплексних потужностей всіх пасивних елементів (тобто резисторів, котушок та конденсаторів) кола.

4.8. Прості кола синусоїдного струму

4.8.1. Коло з послідовним з’єднанням комплексних опорів

Розглянемо коло, утворене шляхом послідовного з’єднання двополюсників з комплексними опорами Z₁, Z₂,...Z_N (рис. 4.41,а). Звичайно, кожен з цих двополюсників може складатися або з одного елемента кола, або з багатьох елементів (але так, щоб це складне коло мало тільки два затискачі).

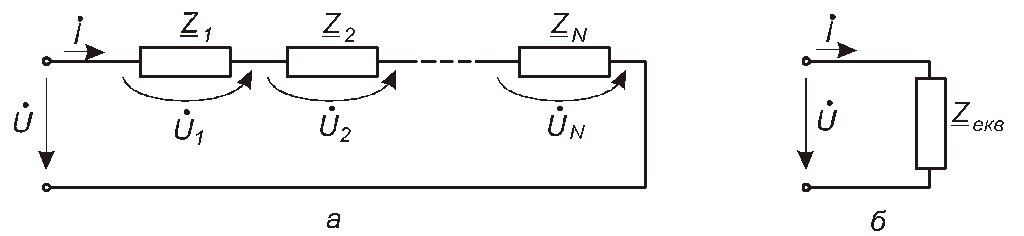
Рис. 4.41

Згідно з другим законом Кірхгофа маємо

Формулу для еквівалентного опору знайдемо, порівнявши останній вираз із формулою, записаною для еквівалентного кола (рис. 4.41,б):

.

Одержуємо, що