Лекція 17

4.6.3. Еквівалентна заміна комплексного опору комплексною провідністю та зворотна заміна

Розглянемо питання взаємозв’язку між комплексним опором та комплексною провідністю пасивної ділянки кола, якого ми частково торкалися в п. 4.6.1 та 4.6.2, але тепер поставимо це питання максимально широко: які співвідношення повинні існувати між активними та реактивними складовими комплексного опору та комплексної провідності пасивної ділянки кола за умови, що напруга на затискачах цієї ділянки та струми крізь ці затискачі є однаковими як при її зображені у вигляді комплексного опору, так і при її зображенні у вигляді комплексної провідності?

Для отримання відповіді на це питання розглянемо дві схеми, зображені на рис.4.36. Вимагатимемо, щоб величини тадля обох кіл були одними й тими самими. Тоді комплексний опір кола, схему якого зображено на рис.4.36,а дорівнює

. (4.25)

З іншого боку, за означенням 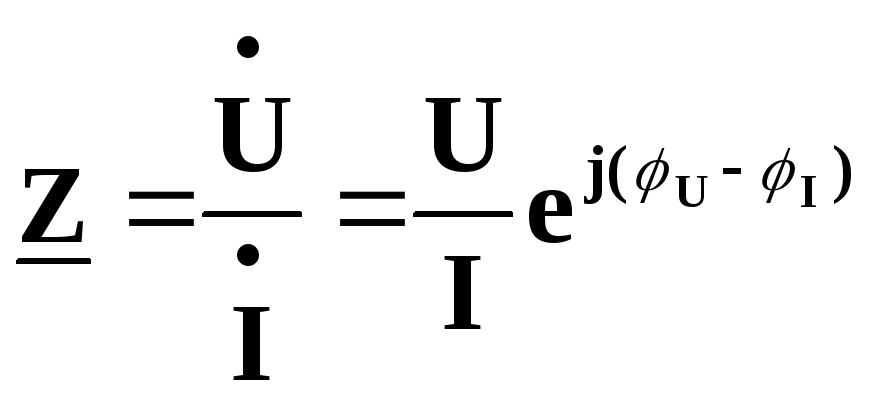. (4.26)

Порівнявши ці вирази, отримуємо, що

. (4.27)

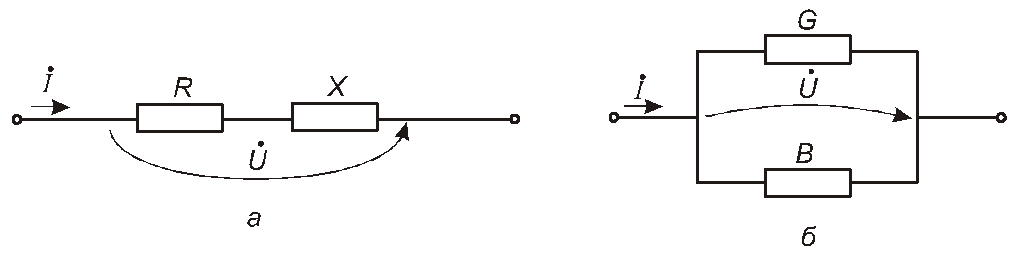
Рис. 4.36

Комплексна провідність кола, схему якого зображено на рис.4.36,б, дорівнює

. (4.28)

З іншого боку, за означенням

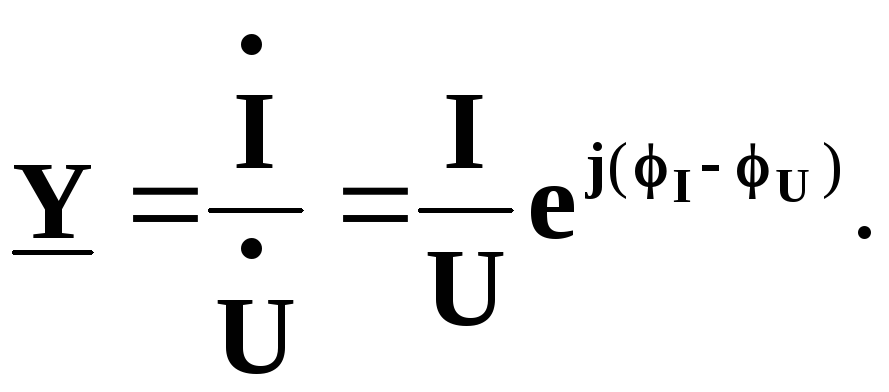(4.29)

Порівнявши (4.28) та (4.29), отримаємо, що

_Y= _I-_U= -(_U-_I). (4.30)

Тепер порівняємо пару виразів (4.27) з парою виразів (4.30). Очевидно, що

Тому немає потреби використовувати окремі позначення _Y та _Z: досить позначити =_U-_I =_Z, тоді _Y= –. В результаті можна записати, що

, (4.31)

де  має фізичний сенс різниці фазового зсуву між напругою та струмом. Водночас з (4.25) та (4.28) випливає, що

.

Тепер з’ясуємо зв’язок між активними та реактивними складовими комплексного опору та комплексної провідності. Нехай відомі величини G та B. Оскільки , тоді:

.

Помножимо чисельник і знаменник правої частини на (G+jB). Матимемо

. (4.32)

Звідси

, (4.33)

. (4.34)

Таким чином, після еквівалентної заміни паралельного кола (рис.4.36,б) на послідовне (рис. 4.36,а), як величина R, так і величина X залежатимуть від частоти, оскільки від неї залежить .

Нехай відомими є величини R та X. Оскільки Y =1/Z, то

.

Помножимо чисельник і знаменник правої частини на (R-jX). Матимемо

.

Звідси

, (4.35)

. (4.36)

Таким чином, після еквівалентної заміни послідовного кола (рис.4.36,а) на паралельне коло (рис.4.36,б), як величина G, так і величина B залежатимуть від частоти, оскільки від неї залежить .

4.6.4. Реальний паралельний коливальний контур

У багатьох практичних випадках реальні властивості паралельного коливального контуру можна досить точно описати, врахувавши активний опір поводу, яким намотано реальну котушку індуктивності, і знехтувавши активною складовою опору реального конденсатора. При цьому електрична принципова схема реального паралельного контуру набуває вигляду, представленого на рис. 4.37,а, де R_k – активний опір дроту, яким виконано котушку, L_k – індуктивність цієї котушки.

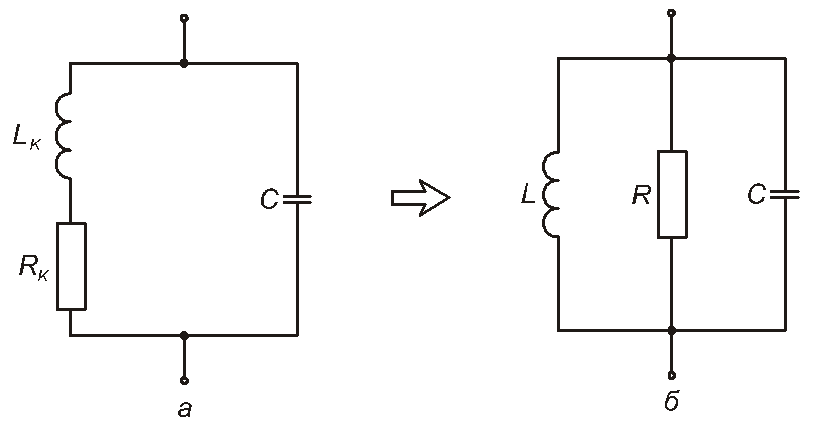
Рис. 4.37

Перейдемо від цієї схеми до більш зручної для розрахунків схеми, зображеної на рис. 4.37,б. Для цього замінимо ліву вітку кола а на еквівалентне з’єднання L та R у колі б, скориставшись співвідношеннями (4.35) та (4.36). Маємо для кола б

.

Вважатимемо, що заміна виконується на резонансній частоті ₀. В пристроях автоматики та зв’язку контури мають велику добротність, тому на цій частоті звичайно ₀L_kR_k і можна записати, що

.

З іншого боку, в колі б індуктивна провідність на частоті ₀ є . Порівнявши два останніх вирази, доходимо висновку, що, тобтоL  L_k. Отже, при переході від кола а до кола б на резонансній частоті індуктивність котушки можна вважати незмінною за умови, що .

Тепер знайдемо величину опору R кола б. Провідність цього резистора G=1/R згідно з формулою (4.35) дорівнює

.

Для реальних контурів з високою добротністю на резонансній частоті ₀ виконується нерівність , тому можна записати, що, звідки. Але ж, як показано раніше, індуктивністьL котушки кола б на резонансній частоті приблизно дорівнює індуктивності L_k котушки кола а. Тоді R(₀L)²/R_k. В підрозділі 4.6.2 ми позначили ₀L= та дали означення добротності паралельного коливального контуру якQ=R/. Тому для реального паралельного коливального контуру маємо змогу записати, що

(4.37)

і що

.

Формула (4.37) дозволяє обчислити опір реального паралельного контуру на резонансній частоті (де він є чисто активним), що потрібно, наприклад, при розрахунку резонансних підсилювачів.

На відміну від кола з паралельним з’єднанням постійних R, L та C (рис. 4.33), у реального паралельного коливального контуру (рис. 4.37,а) резонансна частота ₀ залежить від опору R_k проводу, яким намотано котушку. Одержимо формулу для неї, використавши для кола, схему якого зображено на рис. 4.37,б, умову резонансу струмів:

Розв’язавши ці рівняння відносно ₀, отримаємо

,

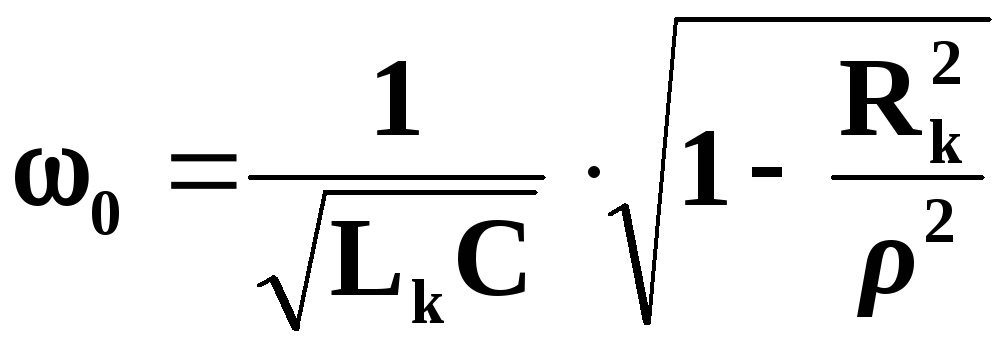де .

Очевидно, що при R_k<< ця формула спроститься до вже відомої: .

Опір реального паралельного коливального контуру суттєво залежить від частоти прикладеної до нього напруги (рис.4.38). Цю властивість широко використовують у пристроях, в яких потрібно відокремити синусоїдні коливання певного діапазону частот від загальної сукупності коливань (так звані фільтруючі кола). З огляду на обмеженість обсягу даного підручника ми не будемо детально обговорювати питання, які постають при підімкненні контуру до джерела сигналу. Зауважимо лише, що для того, щоб резонансні властивості реального паралельного коливального контуру виявилися в повній мірі, необхідно, щоб внутрішній опір R_г джерела сигналу (генератора), підімкненого до цього контуру, був набагато більший величини ²/R_k. Детальне обговорення частотно-виборних властивостей паралельного коливального контуру можна знайти в підручнику [11].

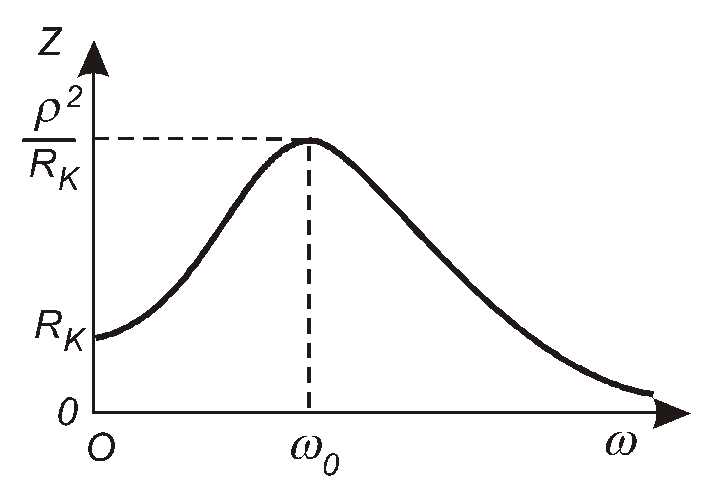
Рис. 4.38