4.5.2. Резонанс напруг. Добротність послідовного коливального контуру

Повернемося до виразу (4.16) для кола, схему якого зображено на рис. 4.27.

де X=X_L-X_C.

Підбираючи величини , L та С, можна добитися того, що реактивні опори індуктивного та ємнісного елементів дорівнюватимуть один одному:

X_L = X_C = X₀. (4.17)

При цьому реактивний опір усього кола дорівнюватиме нулю:

X = X_L – X_C = X₀ – X₀ = 0,

а комплексний опір буде чисто активним і дорівнюватиме величині R:

Z = R + j(X₀-X₀) = R+j0 = R.

Повний опір також дорівнюватиме величині активного опору:

Крім того, з виразу випливає, щоR є мінімальним значенням, яке може приймати величина повного опору. Наприклад, якщо залишити недоторканими L та C і змінювати лише величину , то величина змінюватиметься так, як показано на рис.4.28. РівністьX_L=X_C виконується на деякій кутовій частоті ₀. На цій же частоті аргумент комплексного опору дорівнюватиме нулю:

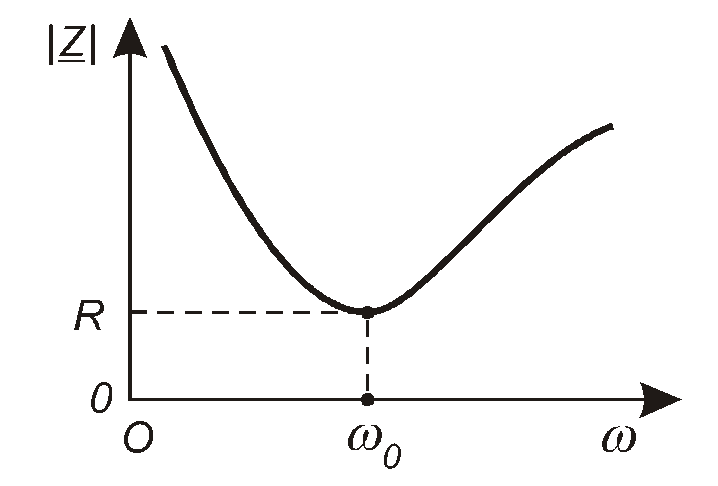
рис. 4.28

У підрозділі 4.5.1 вже показано, що початкова фаза струму обчислюється як , тому при виконанні умовиX_L=X_C маємо:

тобто за вказаної умови струм співпадає за фазою з напругою.

Режим роботи кола, утвореного послідовно з’єднаними індуктивним та ємнісним елементами (наявність резистора не є обов’язковою), при якому реактивний опір кола дорівнює нулю, називається резонансом напруг.

Кутову частоту ₀, на якій має місце резонанс напруг, називають резонансною кутовою частотою.

Коло, схему якого зображено на рис. 4.27, називають послідовним коливальним контуром.

За означенням, при резонансі напруг на частоті ₀маємо, тобтоЗвідси отримуємо дуже важливі для розрахунку пристроїв автоматики та зв’язку формули:

(4.18)

та

. (4.19)

Ці формули визначають величину резонансної частоти через параметри конденсатора та котушки, що складають послідовний коливальний контур.

Згідно з (4.17) та (4.18) маємо:

Величину називаютьхарактеристичним опором послідовного коливального контуру.

Оскільки крізь індуктивний та ємнісний елементи контуру протікає один і той самий струм, то при резонансі маємо рівні діючі значення (або амплітуди) напруг на цих елементах:

.

Але , до того ж при резонансітому в цьому режимі. Тоді.

Введемо добротність послідовного коливального контуру

Тоді при резонансі напруг діюче значення вхідної напруги пов’язане з діючими значеннями напруг на індуктивному та ємнісному елементах як

U_L = U_C = QU.

У пристроях автоматики та зв’язку величина , як правило, набагато більша за R, тому в них Q1. Отже, при резонансі напруг величини напруг на індуктивному та на ємнісному елементах послідовного коливального контуру в Q раз більші ніж вхідна напруга U, що й обумовило назву “резонанс напруг” для розглянутого режиму роботи кола.

Змінюватимемо подумки частоту вхідної напруги при постійних R, L, С та U. Якщо   ₀, то X_L= L   (бо X_L зростає з частотою і сягає величини , коли  досягне ₀), а . При цьому аргумент комплексного опору контуру є від’ємним, бо

Тому початкова фаза струму є більшою за початкову фазу напруги_U. Тобто, при   ₀ струм випереджає вхідну напругу за фазою. Кажуть, що за цієї обставини опір послідовного коливального контуру має ємнісний характер.

Векторні діаграми напруг та струмів для розгляданого випадку   ₀ наведено на рис. 4.29¹. Заштрихований прямокутний трикутник з катетами U_X та U_R і гіпотенузою U називають трикутником напруг.

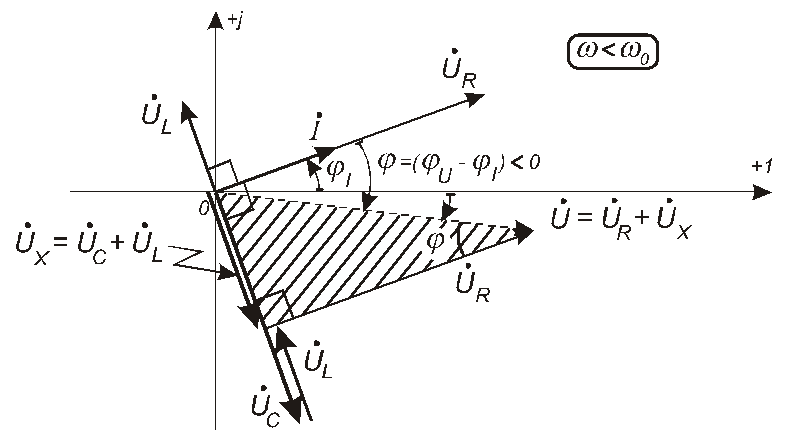
Рис. 4.29

На рис. 4.30 графічно проілюстровані співвідношення між активною та реактивною складовими комплексного опору Z послідовного коливального контуру за умови, що   ₀. Заштрихований на цьому рисунку трикутник називають трикутником опорів. З нього наочно випливає, що .

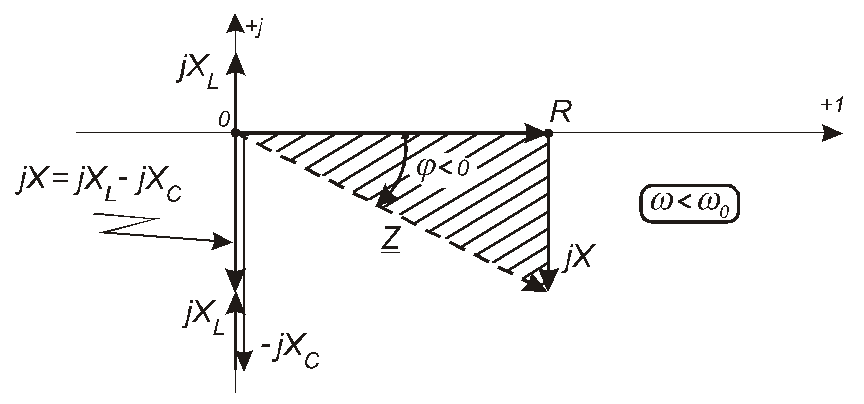
Рис. 4.30

Аналогічним чином для випадку  > ₀ можна показати, що величина  буде додатною і опір послідовного коливального контуру матиме індуктивний характер. Нескладно зробити й графічні побудови, аналогічні показаним на рис.4.29 та рис. 4.30.

У випадку, коли  = ₀ (тобто при резонансі напруг) маємо таjX=j(X_L-X_C)=0, і на відповідних векторних діаграмах залишаються тільки активна складова напругита активний опірR.