4.4. Закони Кірхгофа в символічній формі запису

Розглянемо вузол деякого кола, зображений на рис. 4.25.

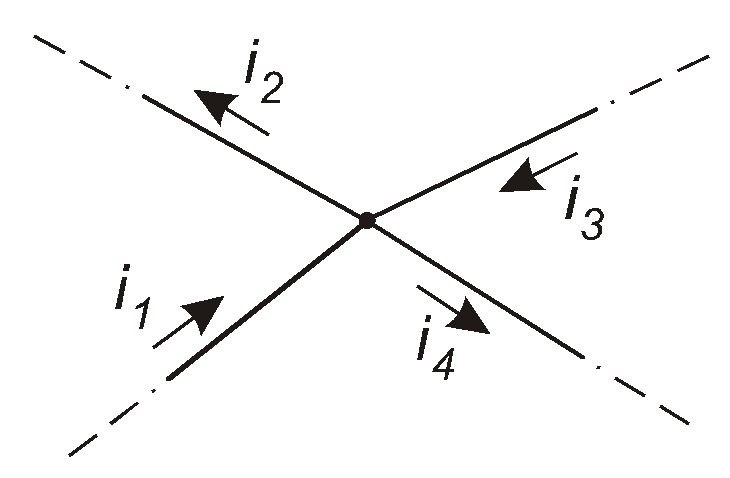
рис. 4.25

Нехай миттєві значення струмів дорівнюють

Їм відповідають такі значення комплексних амплітуд та комплексів діючих значень:

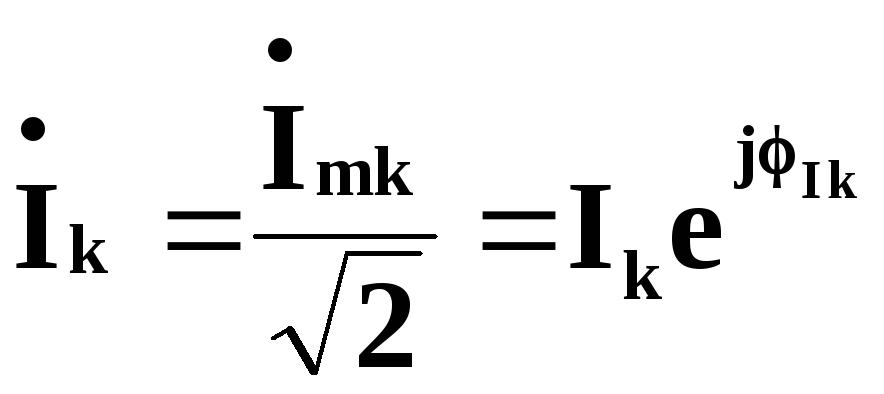, ,k=1,…..,4.

Згідно з першим законом Кірхгофа для миттєвих значень у будь-який момент часу справедлива рівність

i₁ - i₂ + i₃ - i₄ = 0.

Переходячи від неї до комплексних амплітуд та комплексів діючих значень, отримуємо

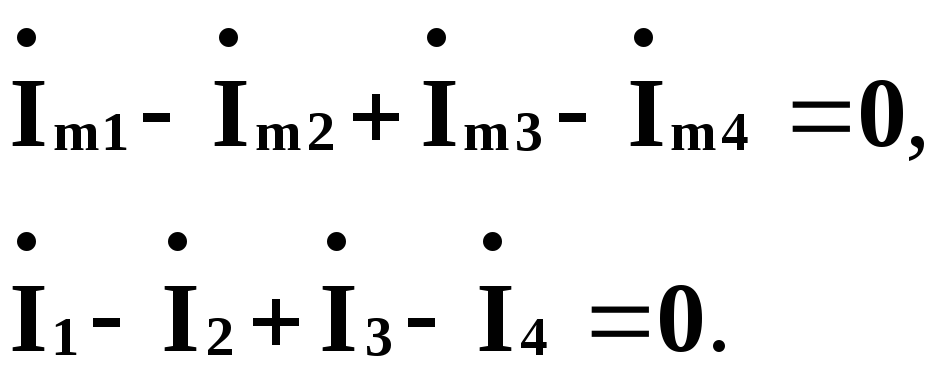
Тобто алгебраїчна сума комплексних амплітуд або комплексів діючих значень струмів у вузлі дорівнює нулю (втікаючі струми входять до цієї суми із знаком “плюс”, а витікаючі – із знаком “мінус”). Або: сума комплексних амплітуд (комплексів діючих значень) струмів, що втікають до вузла, дорівнює сумі комплексних амплітуд (комплексів діючих значень) струмів, які витікають з цього вузла.

Ці ствердження, розповсюджені на довільну кількість віток, що з’єднані в розглянутому вузлі, є першим законом Кірхгофа в символічній формі запису:

де K– кількість вищезгаданих віток.

Розглянемо замкнений контур деякого кола, зображений на рис. 4.26. Нехай миттєві значення ЕРС та струмів відповідно дорівнюють

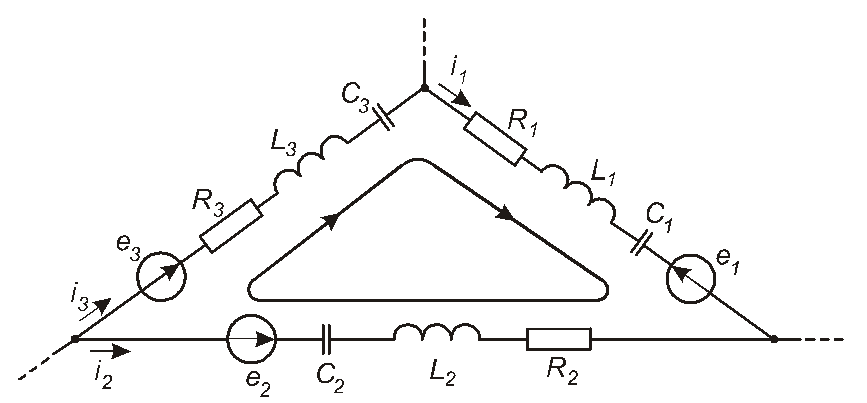
Рис. 4.26

Їм відповідають такі значення комплексних амплітуд та комплексів діючих значень:

, ,

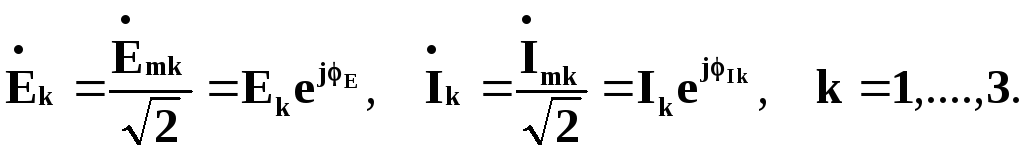
Комплексні опори індуктивних та ємнісних елементів відповідно дорівнюють

Z_Lk=jL_k,

Згідно з другим законом Кірхгофа для миттєвих значень у будь-який момент часу справедлива рівність

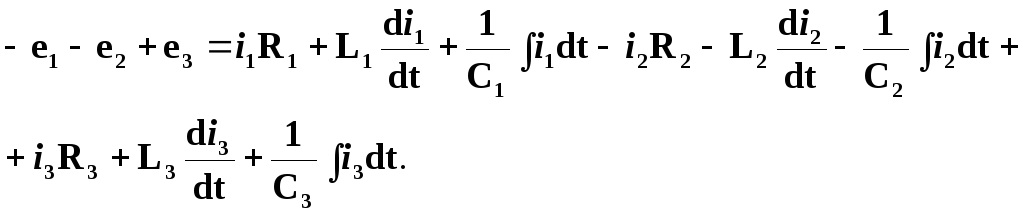
Переходячи від неї до запису для комплексних амплітуд, отримуємо:

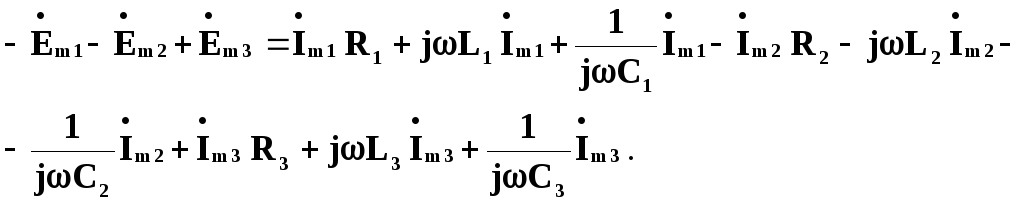
У правій частині стоять вирази для падінь напруги на резисторах., індуктивностяхта ємностях. З урахуванням цього перепишемо останній вираз у такому вигляді:

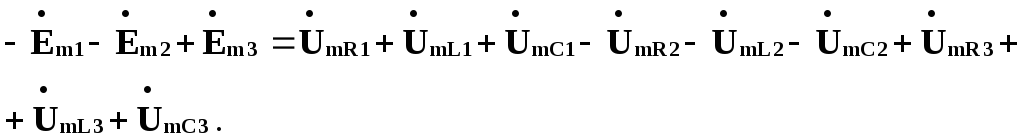
Тобто, в замкненому контурі алгебраїчна сума комплексних амплітуд ЕРС дорівнює алгебраїчній сумі комплексних амплітуд падінь напруг (при цьому ЕРС або падіння напруги входять до цієї суми із знаком “плюс”, якщо їх напрямок співпадає з напрямком обходу контуру, та із знаком “мінус” – якщо не співпадає). Аналогічний висновок відноситься й до комплексів діючих значень ЕРС та падінь напруг. Ці ствердження, розповсюджені на замкнутий контур, утворений довільною кількістю віток, є другим законом Кірхгофа в символічній формі запису.

Лекція 15

4.5. Коло синусоїдного струму з послідовним з’єднанням активного, індуктивного та ємнісного елементів

4.5.1. Основні співвідношення. Комплексний опір

Розглянемо коло, схему якого зображено на рис. 4.27.

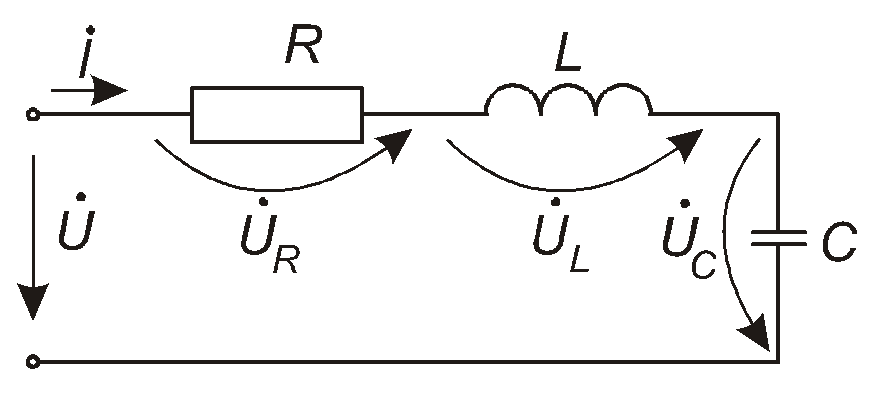
Рис. 4.27

Вважатимемо відомими величини R, L та С а також амплітуду, частоту та початкову фазу вхідної напруги . Необхідно визначити амплітуду та початкову фазу струму, який протікає в цьому колі (частота цього струму дорівнює частоті вхідної напруги, оскільки коло лінійне).

Запишемо рівність згідно з другим законом Кірхгофа для комплексів діючих значень напруг:

Виразимо напруги через струм та відповідні опори:

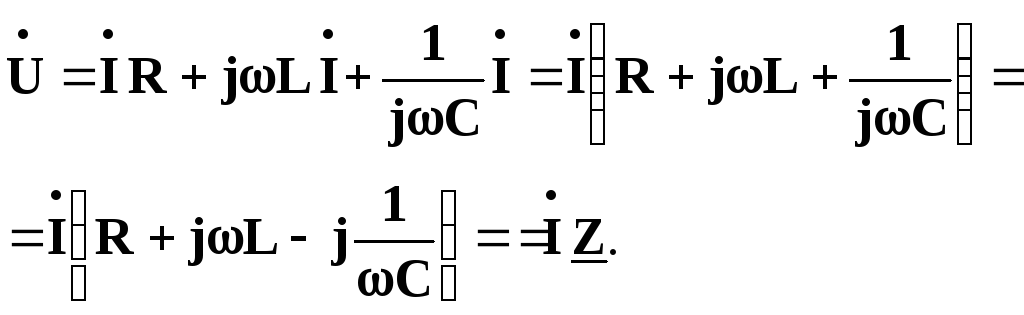(4.15)

Тут

(4.16)

є комплексним опором даного кола.

Величина R є активним опором кола, а величина X=X_L-X_C є реактивним опором цього кола. Приведемо вираз (4.15) до показникової форми:

Величину називаютьповним опором кола, а кут  – аргументом комплексного опору кола.

З виразу (4.15) випливає, що

З іншого боку вираз для комплексу діючого значення струму має вигляд Порівнявши два останніх вирази, доходимо висновку, що

Частота струму, звичайно ж, є такою, яка й частота вхідної напруги. Амплітуда струму обчислюється як I_m=I2. Отже, задачу розрахунку параметрів струму розв’язано.

Розглянемо тепер одну важливу властивість, притаманну колу з послідовним з’єднанням активного, індуктивного та ємнісного елементів.