4.3. Пасивні елементи кола синусоїдного струму

4.3.1. Резистор (активний опір)

Нехай є деякий резистор R, крізь який протікає синусоїдний струм. Цей струм створює на резисторі падіння напругиu. За законом Ома маємо

(4.5)

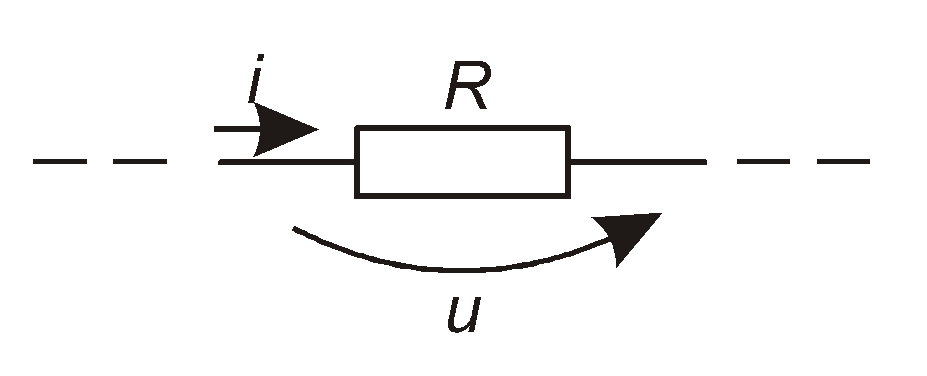
Рис. 4.6

Але з іншого боку . Порівнявши два останніх вирази, отримаємо, що для резистора

.

Таким чином, напруга на резисторі та струм у ньому співпадають за фазою (рис. 4.7).

Тепер перейдемо до символічної форми запису. Виразові (4.5) для миттєвих значень відповідає таке співвідношення між комплексною амплітудою струму та комплексною амплітудою напруги:

,

де причому_U=_I.

Тобто

.

Відповідну векторну діаграму наведено на рис. 4.8.

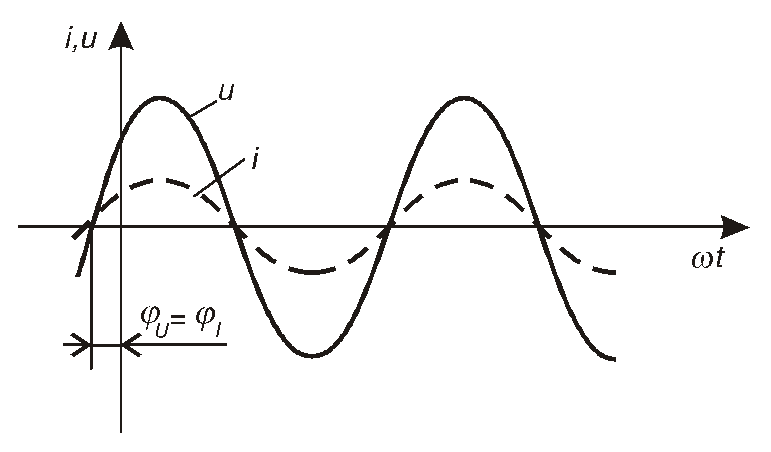
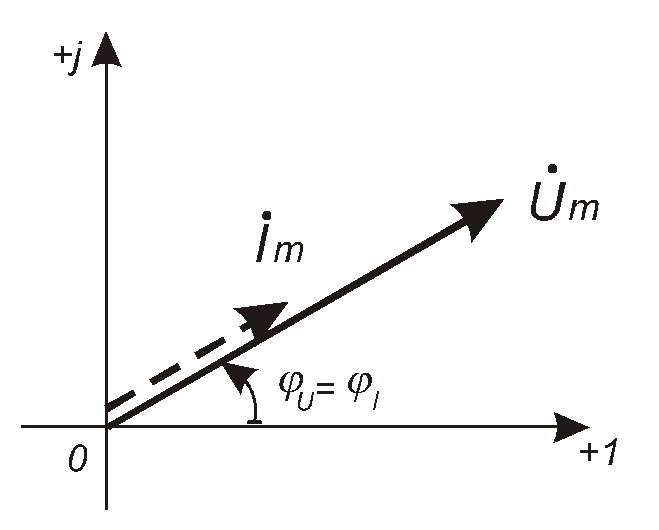
Рис. 4.7 Рис. 4.8

Миттєва потужність, споживана резистором, дорівнює добутку миттєвих значень напруги та струму

.

Підставивши сюди вирази для миттєвих значень, отримаємо:

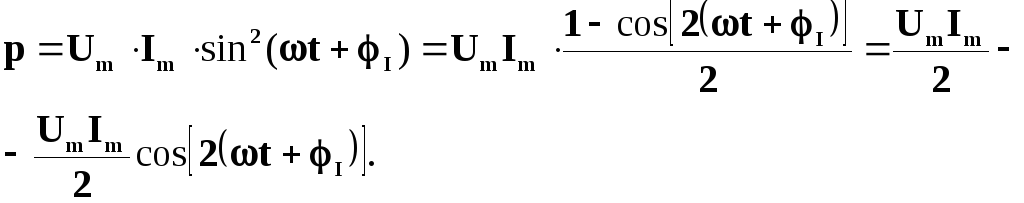
Згідно з цим виразом, миттєва потужність змінюється в часі так, як це зображено на рис. 4.9.

Активна потужність (тобто та потужність, яка необоротно споживається колом) є середнім за період значенням миттєвої потужності:

.

Другий інтеграл дорівнює нулю як інтеграл від косинуса за час, кратний періоду (нагадуємо, що =2/Т). Тому:

.

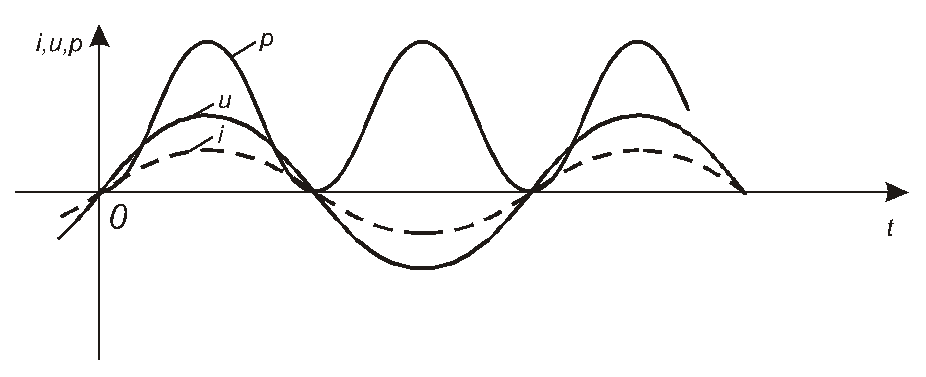
Рис. 4.9.

Якщо ж перейти до діючих значень ( ), то отримаємо, що

P=UI.

Лекція 13

4.3.2. Індуктивний елемент

Індуктивний елемент – це ідеалізований елемент електричного кола, який має властивість оборотно накопичувати енергію магнітного поля, а також утворювати на своїх затискачах ЕРС при зміні магнітного потоку крізь себе.

Типовим прикладом індуктивного елемента є котушка індуктивності, намотана ідеальним проводом, який має активний опір, що дорівнює нулю.

На рис. 4.10 наведене спрощене зображення такої котушки (показані тільки три витки із загальної кількості Wвитків). Умовне позначення індуктивного елемента наведене на рис. 4.11.

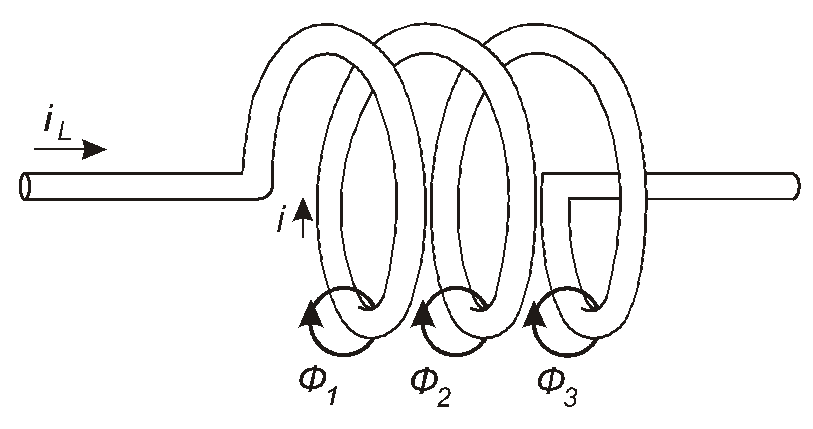
Рис. 4.10

Рис. 4.11

Нехай в котушці протікає струм довільної форми, миттєве значення якого дорівнює i. Завдяки цьому кожен виток котушки створює свій магнітний потікФ_к. Кажуть, що цей магнітний потік зчеплений зk-м витком. Власне потокозчеплення всієї котушки знаходять як суму потоків усіх витків:

.

Одиницею вимірювання величини є вебер (Вб).

Коефіцієнт пропорційності Lміж власним потокозчепленням ідеальної котушки та струмом, який його викликав, називаютьіндуктивністю котушки:

звідки L=/i_L.

Індуктивність вимірюють у генрі (Гн), при цьому 1 Гн=1 Вб / 1 А¹⁾.

У лінійному колі величина Lє постійною і визначається лише формою та геометричними розмірами котушки (діаметри котушки та проводу; довжина котушки, крок намотування і т. ін.) і відносною магнітною проникністю речовини, в якій розташовано котушку.

При зміні в часі струму iпропорційно змінюється й величина.

Закон електромагнітної індукції говорить, що при цьому в котушці наводиться ЕРС самоіндукції, миттєва величина якої дорівнює

.

Знак “мінус” вказує, що e_Lспрямована так, щоб протидіяти зміні струму, яка викликала цю ЕРС (це - правило Ленца).

1) На практиці використовують також часткові одиниці: мілігенрі (мГн) та мікрогенрі (мкГн), причому 1 мГн=10^-3 Гн, 1 мкГн=10^-6 Гн.

За традицією прийнято, щоб на схемі співпадали напрямки i_Lта e_L, а такожi_Lтаu_L(рис. 4.12).

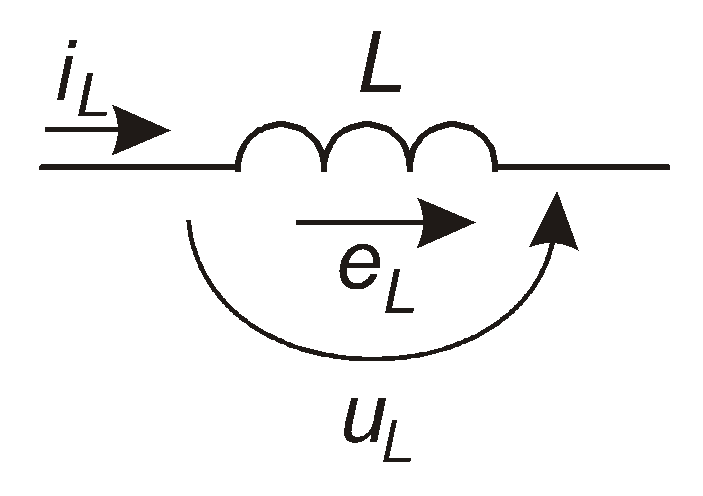
Рис. 4.12

Тоді за другим законом Кірхгофа напруга на ідеальній котушці за будь-якої залежності струму i_L(t) від часу дорівнює:

.

Якщо струм синусоїдний, то

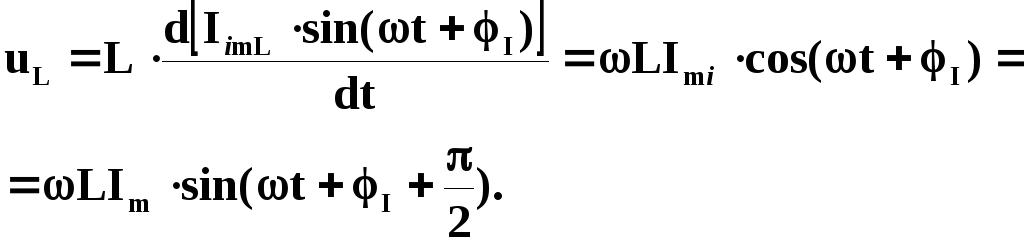(4.6)

Але з іншого боку Порівнявши два останніх вирази, отримаємо, що для індуктивності

(4.7)

Таким чином, напруга на індуктивному елементі (тобто на ідеальній котушці) прямо пропорційна не тільки силі струму крізь цю котушку, але ще й індуктивності котушки та частоті сигналу. Величину

називають реактивним опором котушки. Він прямо пропорційний частоті (рис. 4.13). Отже, можна записати, що

,

або для діючих значень напруги та струму:

.

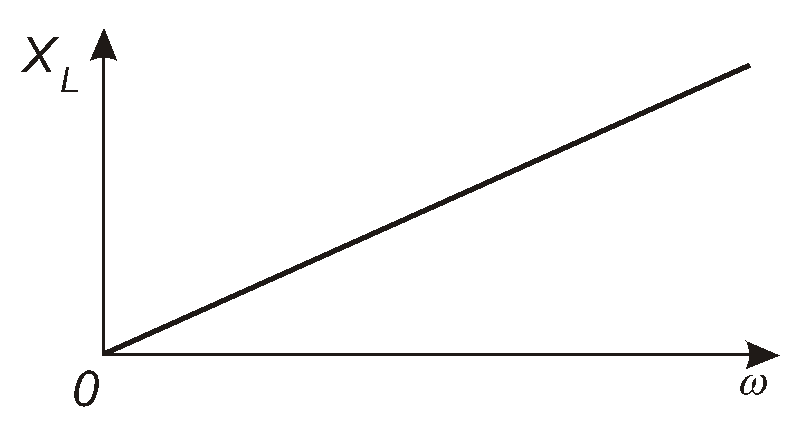
Рис. 4.13

Вираз (4.7) означає, що напруга на ідеальній котушці випереджає за фазою струм у ній на/2(рис.4.14).

Тепер перейдемо до символічної форми запису. Виразові (4.5) для миттєвих значень відповідає таке співвідношення між комплексною амплітудою струму та комплексною амплітудою напруги:

, (4.8)

де причому.

Тобто

.

Відповідну векторну діаграму наведено на рис. 4.15.

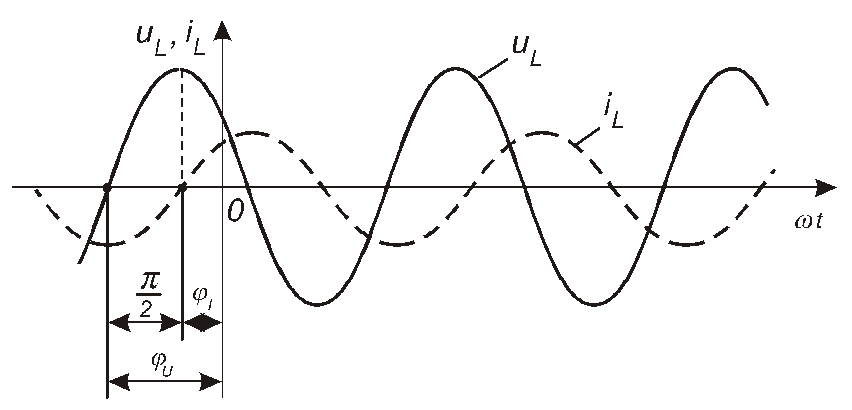
Рис. 4.14

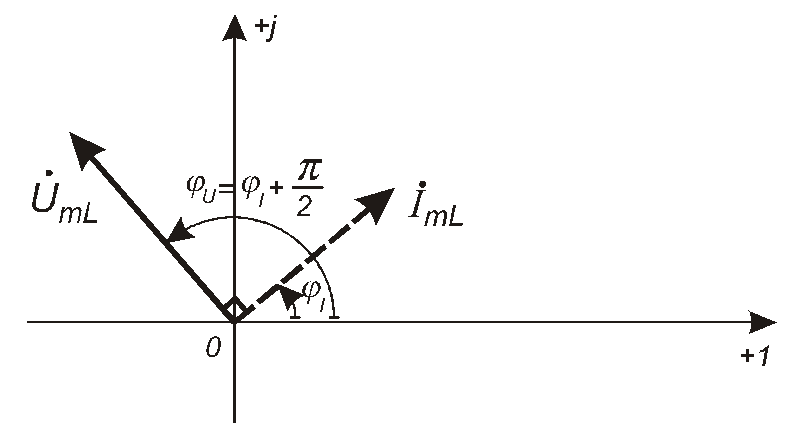
Рис. 4.15

Величину

Z_L=jL=jX_L,

яка фігурує у виразі (4.8), називають комплексним опоромідеальної котушки (індуктивного елемента). Це чисто умовна величина. Отже, можна записати, що

,

або для комплексів діючих значень напруги та струму, що

.

Залежність Z_L()на комплексній площині ілюструє рис. 4.16.

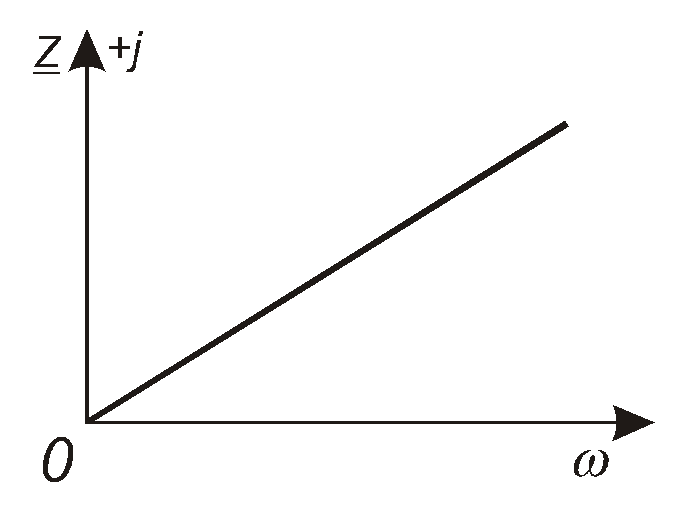
Рис. 4.16

Миттєва потужність, споживана індуктивним елементом, є

p_L=u_Li_L.

Підставивши сюди вирази для миттєвих значень напруги та струму, отримаємо:

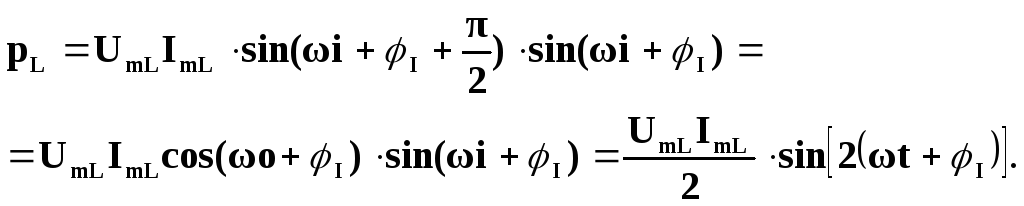
Згідно з цим виразом, миттєва потужність в індуктивному елементі змінюється в часі так, як це показано на рис. 4.17.

Активна потужність є середнім за період значенням миттєвої потужності:

.

Оскільки =2/Т, то цей інтеграл дорівнює нулю як інтеграл від синуса за час, кратний періоду. Томуактивна потужність, споживана індуктивним елементом, дорівнює нулю: P_L=0.

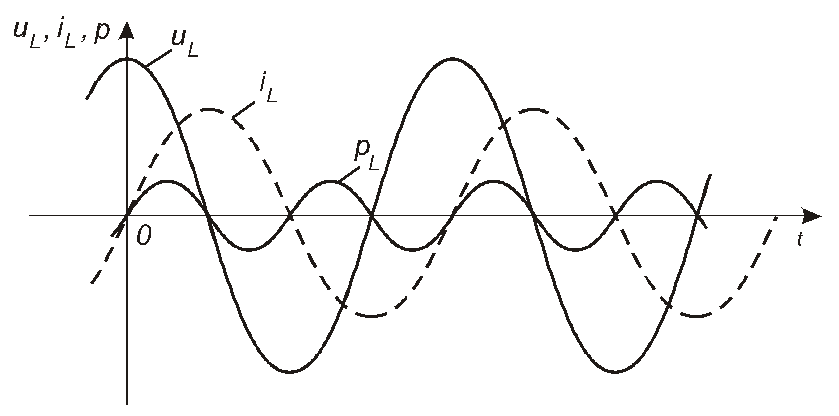
Рис. 4.17

Неважко показати, що енергія, накопичена в індуктивному елементі з моменту часу t=0по деякий поточний момент часуt=, дорівнює. Звідси випливає, що ця енергія періодично змінюється від величинив моменти максимального накопичення до нуля в моменти, коли індуктивний елемент повернув усю накопичену енергію в зовнішнє коло.