4.2.3. Комплекси струмів, напруг та ерс. Векторна діаграма. Суть символічного методу розрахунку

Розглянемо деякий обертовий вектор . Записавши комплексну експоненту за формулою Ейлера, отримаємо

. (4.3)

Якщо I_mмає фізичний сенс амплітуди деякого струму,– його кутової частоти, а_I– його початкової фази, то можна зробити висновок, що миттєве значення синусоїдного струмує проекцією введеного вище обертового вектораАна вісь уявних чисел, тобто. Звідси випливає, що будь-якому синусоїдному струмові можна зіставити індивідуальний обертовий вектор, який однозначно зв’язаний з цим струмом. Звичайно цей обертовий вектор позначають , поставивши крапку над позначенням миттєвої величини струму:

(4.4)

Величину називаютькомплексом миттєвого значення струму. Він є символічним зображенням реального синусоїдного струму, а відповідний обертовий вектор на комплексній площині є символічним графічним зображенням цього ж струму.

Вираз (4.4) може бути записаний у дещо іншому вигляді

,

де – так званакомплексна амплітуда струму.

У розрахунках також використовують комплекс дійсного значення синусоїдного струму

,

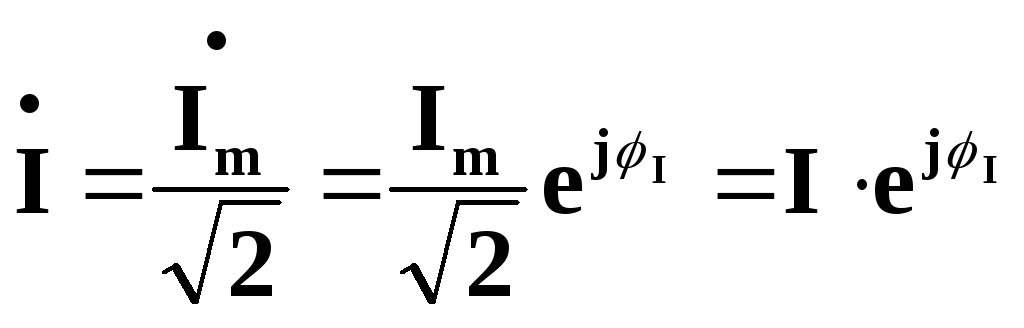де I– діюче значення струму (див. п. 4.1 3).

Аналогічно тому, як це було зроблено для струмів, вводять обертові вектори напруги та ЕРС, а також комплекси їх миттєвих значень та, де– комплексна амплітуда напруги,

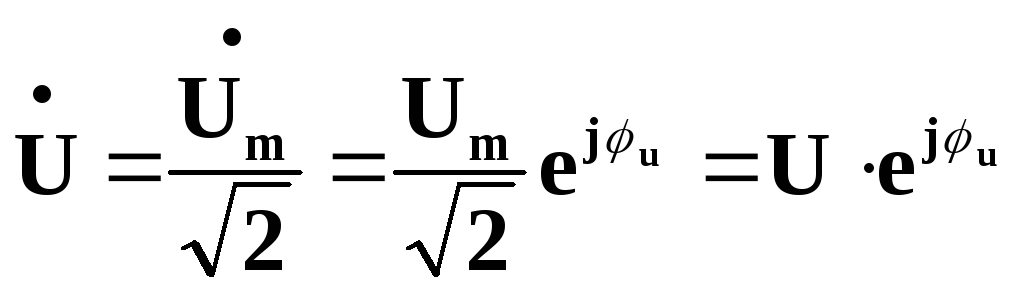– комплекс діючого значення напруги,

– комплексна амплітуда ЕРС,

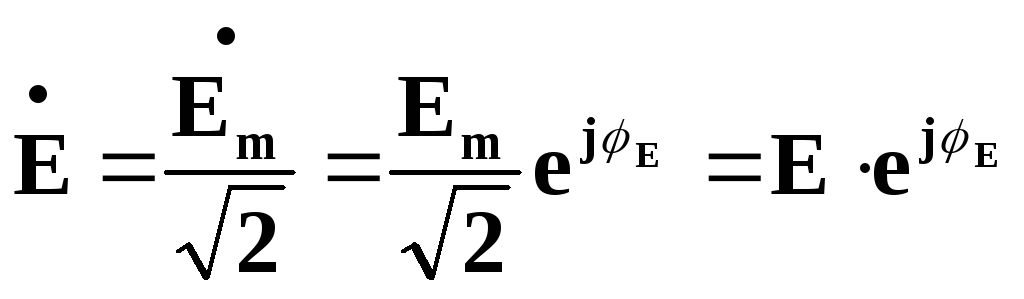– комплекс діючого значення ЕРС.

Якщо є кілька векторів (наприклад, ,та), які обертаються з однаковою кутовою частотою, то один відносно одного вони нерухомі. Тому в цьому випадку наявність обертання достатньо тільки мати на думці, а на комплексній площині слід зображувати розташування цих векторів приt=0.

Таке зображення синусоїдних струмів, напруг та ЕРС, як векторів на комплексній площині, називають векторною діаграмоювідповідно струмів, напруг або ЕРС.

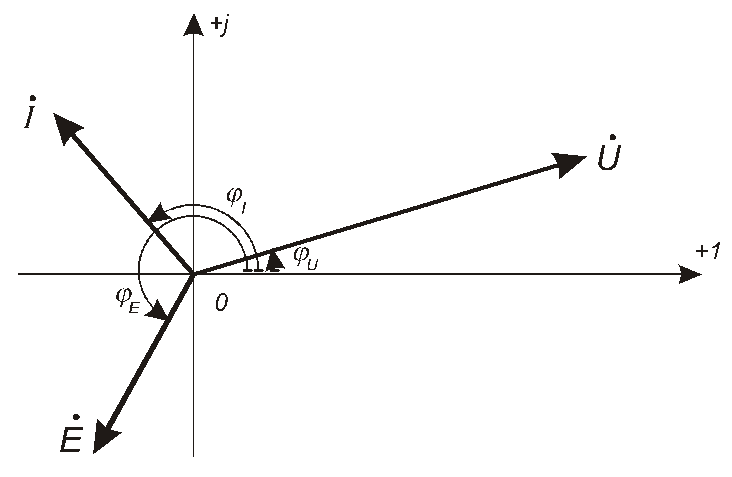
Рис. 4.5

Наприклад, на рис. 4.5 зображено векторну діаграму комплексів діючих значень (векторна діаграма може бути побудована і для комплексних амплітуд; різниця буде тільки в довжині векторів – вони будуть у 2разів довші). Нагадаємо, що напрямок позитивного відліку кута – проти годинникової стрілки.

У читача може виникнути питання: навіщо замінювати, наприклад, опис напруги у вигляді синусоїдної функції часу, яку можна наочно побачити на екрані осцилографа (приладу, який зображує розвиток електричних процесів у часі), на якийсь абстрактний вектор на комплексній площині або на комплексну амплітуду?

Відповідь полягатиме в такому. Якщо описувати струми, напруги та ЕРС кола виключно у вигляді їх миттєвих значень (наприклад, ), то й систему рівнянь за законами Кірхгофа, потрібну для обчислення шуканих струмів (або інших величин) складати треба теж для миттєвих значень. Але тоді в процесі розв’язання цієї системи рівнянь виникне потреба в громіздких тригонометричних перетвореннях. Перехід до комплексних амплітуд або комплексів діючих значень струмів, напруг та ЕРС дозволяє, як це побачить читач на наступних сторінках цього підручника, при розрахунку кола методом рівнянь Кірхгофа (або будь-яким іншим методом) складати необхідні рівняння та виконувати обчислення точнісінько так само, як це робилося для кіл постійного струму, тобто на базі звичайних алгебраїчних прийомів. “Платою” за цю зручність є необхідність використовувати для позначення коливань та опорів дещо нову символіку (наприклад,замістьU,замістьI,ZзамістьRі т. д). Заміна миттєвих значень електричних коливань, а також опорів, на їх символічні зображення з подальшим складанням та розв’язанням звичайних алгебраїчних (а не тригонометричних) рівнянь кола складає сутьсимволічного (іноді його звуть комплексним)методурозрахунку електричних кіл синусоїдного струму.

Існують певні обмеження застосування символічного методу, а саме: його можна застосовувати для розрахунку тільки тих кіл, в яких не відбувається нелінійних перетворень миттєвих значень електричних коливань. Прикладами нелінійних перетворень є логарифмування коливання, множення двох коливань і т. ін. Але доки ми розглядатимемо лінійні електричні кола на ці обмеження можна не звертати уваги.

Дещо детальніше про математичні основи символічного методу розрахунку кіл та про властиві йому обмеження можна дізнатися з класичної праці [10].