4.2.2. Основні відомості про комплексні числа

Комплексне число – це число виду А=а+jв, деатав– дійсні числа, аj=-1– так звана уявна одиниця. Величинуаназивають дійсною частиною комплексного числа (умовне позначення а =Re{A}), величинувназивають уявною частиною комплексного числа (умовне позначенняв= Im{A}). В радіоелектроніці комплексне число позначають літерою з підкреслюванням.

Вираз Аявляє собоюалгебраїчну форму запису комплексного числа. Розглянемо площину з декартовими прямокутними координатами, в яких вісь абсцис є віссю дійсних чисел, а вісь ординат – віссю уявних чисел. З алгебраїчної форми запису випливає графічне зображення комплексного числаАу вигляді точки з координатами (а,в) (рис.4.2).

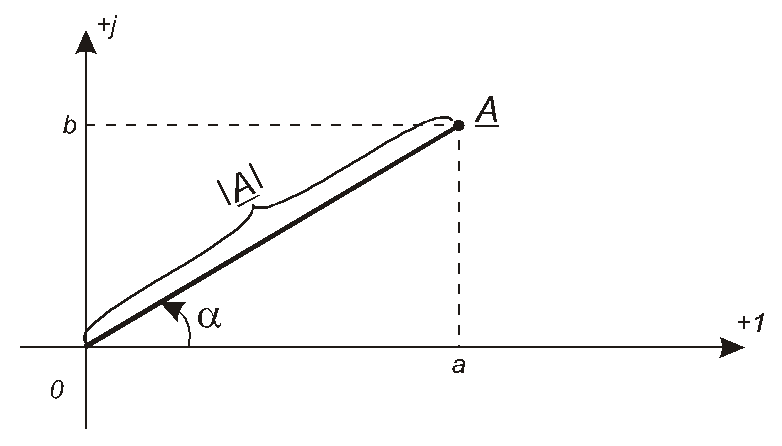
Рис. 4.2

Розглянемо нижній з двох прямокутних трикутників, наявних на рис.4.2. Довжина катета, який розташовано на осі дійсних чисел, дорівнює а, а довжина катета, який розташовано на осі уявних чисел, дорівнюєв,тому гіпотенузаОАдорівнює. Позначимо її як. Ця гіпотенуза утворює кутз віссю дійсних чисел, тому з того ж прямокутного трикутника випливає, що=cos,в=sin, а отже

.

Останній вираз називають тригонометричною формою запису комплексного числа, величинуназиваютьмодулем абоабсолютною величиною комплексного числа, а величину–аргументомкомплексного числаА.

Використання формули Ейлера

дозволяє перейти від тригонометричної форми запису комплексного числа до його показникової (експоненціальної) форми запису

.

Звідси випливає ще один спосіб графічного зображення комплексного числа – його зображення у вигляді вектора довжиною , спрямованого під кутомдо позитивного напрямку осі дійсних чисел.

Для переходу від алгебраїчної форми запису до показникової форми запису використовують такі співвідношення:

;

Отже, Числоназиваютькомплексно-спряженим числуА, якщо .

Додавання та віднімання комплексних чисел виконують, попередньо привівши їх до алгебраїчної форми запису:

;

;

.

Ці операції можна також виконати графічно (з точністю, обмеженою точністю графічних побудувань), користуючись правилами додавання та віднімання векторів (рис. 4.3).

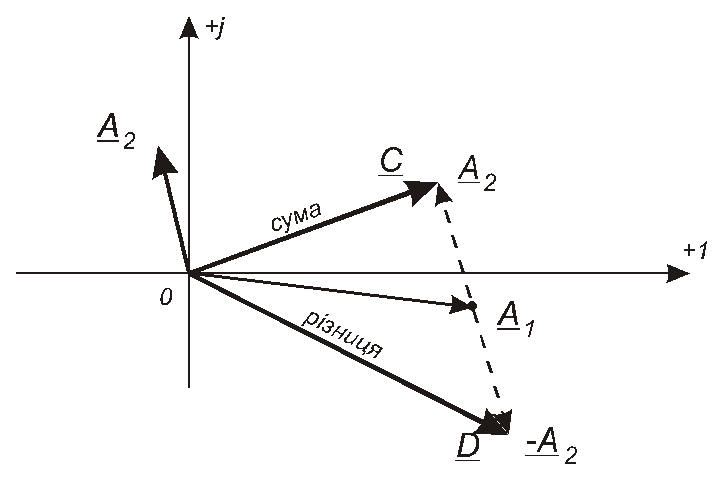
Рис. 4.3

Множення комплексних чисел виконують як в алгебраїчній, так і в показниковій формі запису:

де jj= - 1;

.

Ділення комплексних чисел теж можна виконувати як в алгебраїчній, так і в показниковій формі запису.

.

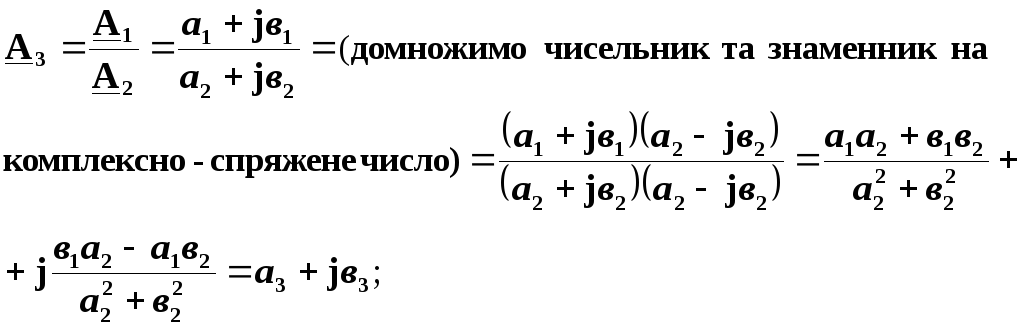
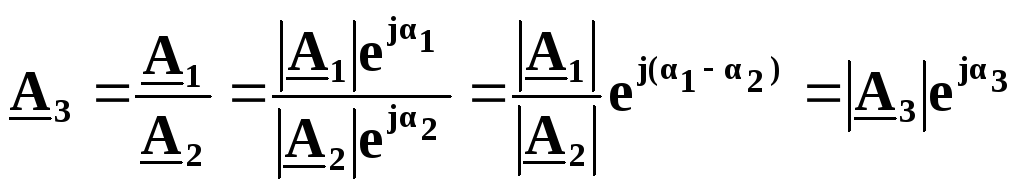Звичайно множення та ділення зручніше виконувати в показниковій формі запису.

Зауважимо, що згідно з формулами Ейлера, маємо:

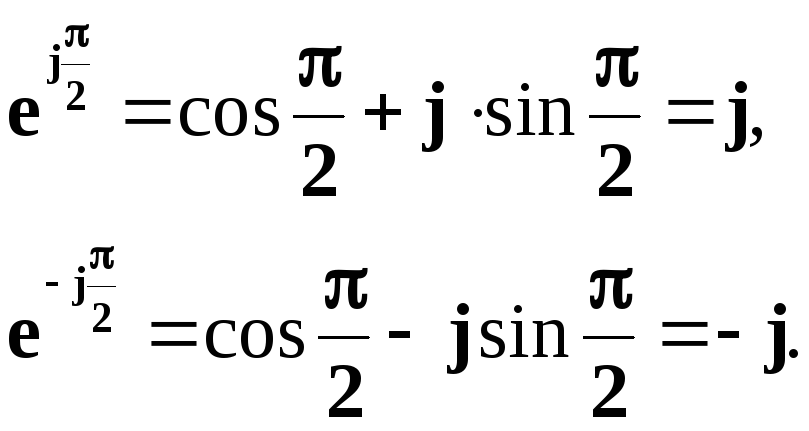
Тоді

.

Звідси випливає, що множення числа Анаj(або, що те ж саме, на) призводить до того, що вектор добутку утворюється з вектораАшляхом повороту останнього напроти годинникової стрілки без зміни довжини вектора. Множення ж на (-j) числаА(або, що те ж саме, його множення на) утворює вектор добутку шляхом повороту вектораАназа годинниковою стрілкою.Ці результати ілюстровані рис. 4.4.

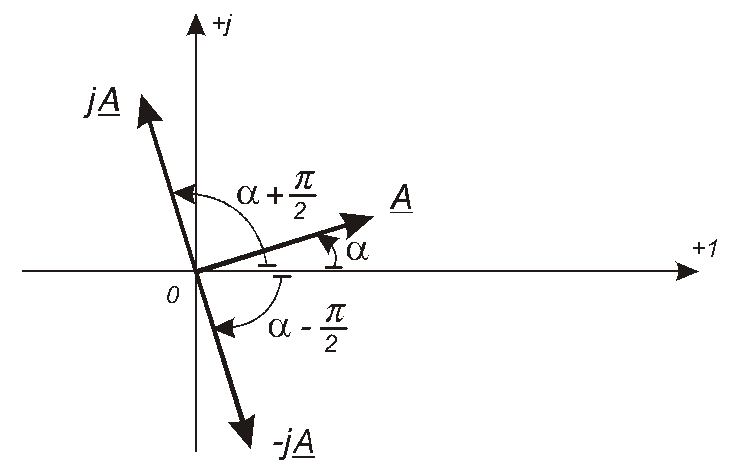
Рис. 4.4

Взагалі, множення комплексного числа на призводить до повороту вектора, який зображує це число, на кутпроти годинникової стрілки, якщо0, або за годинниковою стрілкою, якщо,0.

Отже, якщо кут повороту є пропорційним часу, тобто = t, то множення комплексного числаАнапризведе до утворення нового вектора, який являє собою той же векторА, який безупинно обертається проти годинникової стрілки з кутовою частотою, – так званий обертовий вектор.