Лекція 10

3.6. Розрахунок нерозгалуженого магнітного кола

3.6.1. Пряма задача

Нехай відомі геометричні розміри магнітного кола (рис. 3.8 та 3.9), матеріал магнітопроводу (тобто відома основна крива намагнічування) та магнітний потік Фабо індукціяВу зазорі. Треба знайти величину МРС (або струм у котушці при відомому числі витківW).

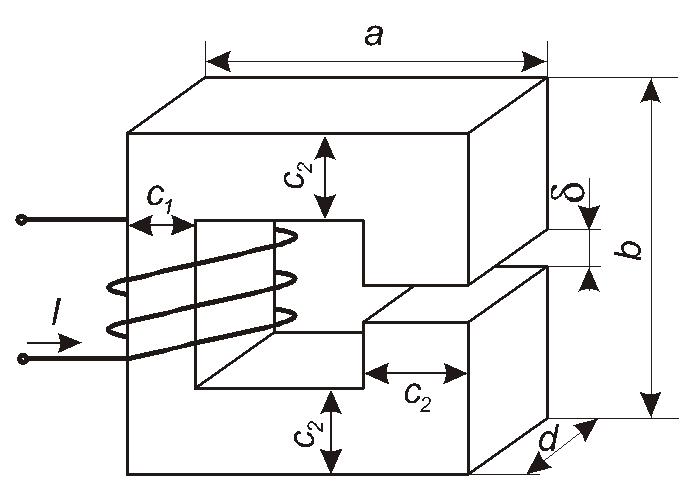
Рис. 3.9

При розв’язанні задачі спочатку знаходимо індукцію в кожній з ділянок магнітного кола:

Потім за основною кривою намагнічування знаходимо величини Н₁таН₂(рис. 3.10).

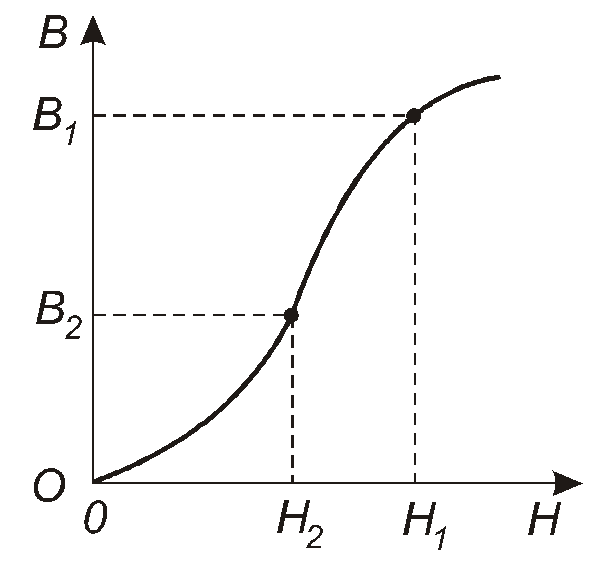
Рис. 3.10

Далі обчислюємо напруженість поля в зазорі як (в амперах на метр).

За відомими розмірами осердя знаходимо довжини ділянок магнітного кола. Нарешті, обчислюємо шукану величину МРС як

.

3.6.2. Зворотна задача

Нехай відомі геометричні розміри магнітного кола (рис. 3.8 та 3.9), матеріал магнітопроводу (тобто відома основна крива намагнічування) та величина F₀магніторушійної сили. Треба знайти величинуФ₀магнітного потоку в колі.

На початку розв’язання зобразимо електричне коло – аналог магнітного кола, зображеного на рис. 3.8. Цей аналог поданий на рис. 3.11.

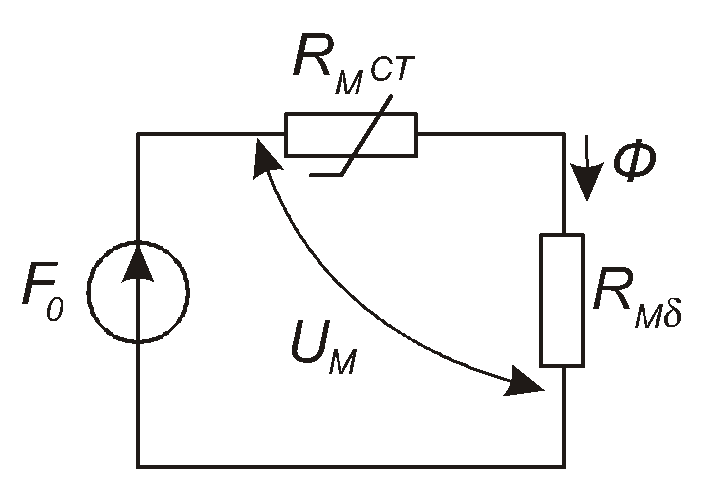
Рис. 3.11

Зазначимо, що магнітний опір R_мстосердя (електротехнічної сталі) є нелінійним, бо у виразі (3.6) фігурує величина, яка залежить відН, а отже – і від потокуФ. Магнітний опір зазоруR_мбне залежить відФ, оскільки його величина утворюється з (3.6) при=1 (відносна магнітна проникність повітря).

Щоб раціонально обмежити діапазон розрахунків, обчислимо максимально можливу величину Ф_maxмагнітного потоку в колі, схему якого зображено на рис. 3.11. Для цього припустимо, що магнітопровід ідеальний, тобтоR_мст=0. Тоді

.

Після цього виберемо на інтервалі [0, Ф_max] близько 10 розрахункових точок, розташованих з кроком приблизно 0,1Ф_max. Для кожного з цих значеньФ_kобчислимо величинупадіння магнітної напруги на пасивній частині кола, схему якого зображено на рис. 3.11.

Тепер за сукупністю обчислених точок (Ф_k,)побудуємовебер-амперну характеристику (ВбАХ) магнітного кола –залежність магнітного потоку в колі від величини прикладеної до цього кола магнітної напруги (рис. 3.12).

Оскільки величина магнітної напруги, прикладеної до пасивної частини кола, дорівнює F₀, то, відклавши на осі магнітних напруг величинуF₀, проведемо крізь неї вертикаль і знайдемоФ₀як величину потоку, що відповідає точці перетину ВбАХ з цією вертикаллю (рис. 3.12).

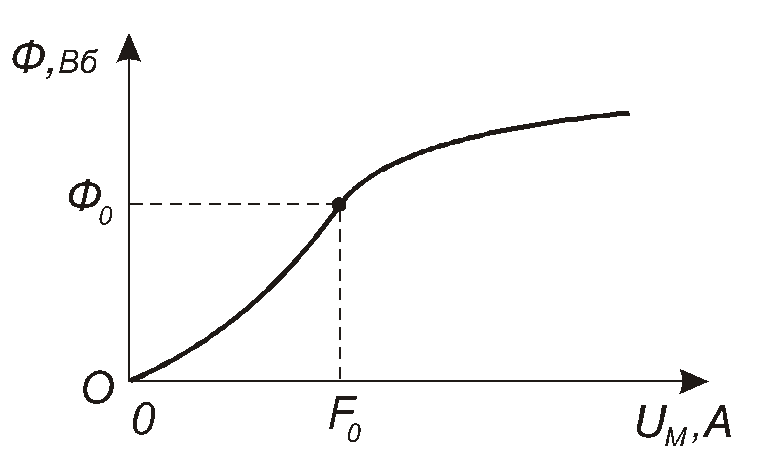
Рис. 3.12

3.7. Перший закон Кірхгофа для магнітних кіл

Оскільки кожна лінія індукції магнітного поля замкнена сама на себе, то кількість цих ліній, які входять у будь-яку замкнену поверхню, що знаходиться в магнітному полі,дорівнює кількості ліній, яківиходятьз цієї поверхні. Тобто сумарний магнітний потік крізь замкнену поверхню дорівнює нулю. Уявімо собі, що деяка замкнена поверхня охоплює місце зчленування кількох стрижнів осердя, в кожному з яких протікає свій магнітний потікФ_k. Тоді можна зробити висновок, що

, (3.7)

де K– кількість зчленованих стрижнів.

Величина потоку входить до цієї суми із знаком “плюс”, якщо цей потік втікає в місце зчленування (вузол магнітного кола), та із знаком “мінус” –якщо потік витікає.

Приклад

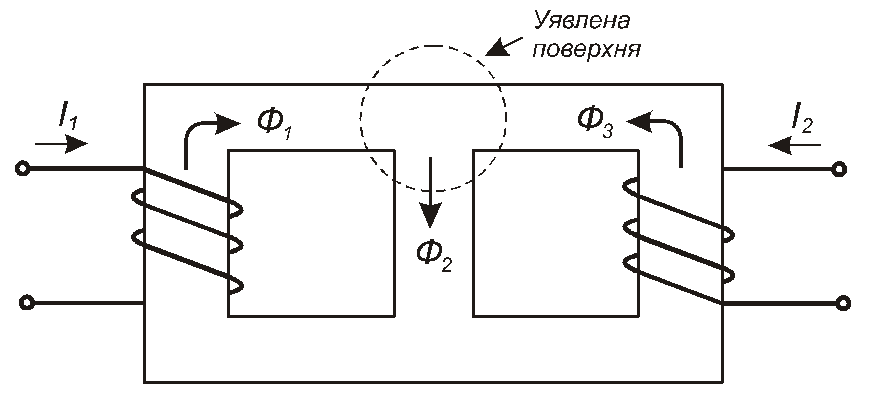
Рис. 3.13

Для магнітного кола, схематично зображеного на рис. 3.13, маємо

Ф₁-Ф₂+Ф₃=0

або

Ф₂ = Ф₁+Ф₃ .