3.4. Закон повного струму

Розглянемо одиночний прямий провідник, нескінченної довжини, яким протікає струм (фрагмент провідника на рис. 3.5). Як відомо з курсу фізики силові лінії магнітного поля, утворюваного таким провідником, являють собою концентричні окружності, площина яких перпендикулярна цьому провіднику. Вектор напруженості магнітного поля в будь-якій точці простору є дотичною до відповідної окружності. Напрям вектора визначається за правилом гвинта із правою різзю (рис.3.5), також відомим з курсу фізики.

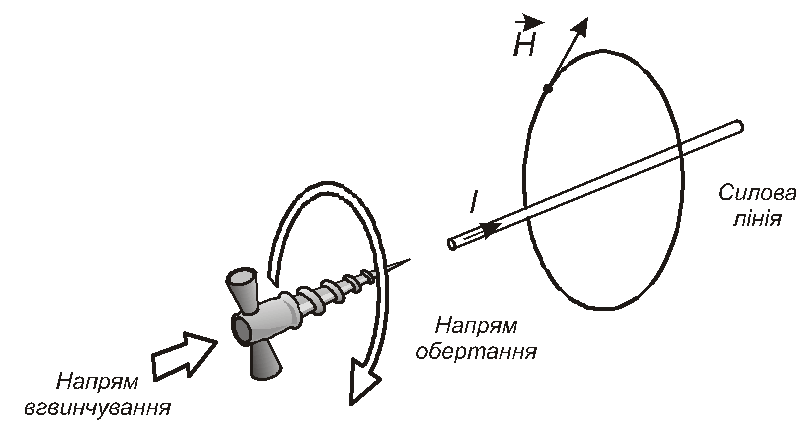
Рис. 3.5

Тепер нехай є кілька провідників, в яких протікають струми (рис. 3.6). Охопимо їх довільним замкненим контуром L. Будемо обходити цей контур у напрямку, який вказаний елементарним дотичним вектором. Згідно з експериментально встановленимзаконом повного струму, має місце таке співвідношення:

, (3.3)

де W– кількість струмів, охоплених контуром L.

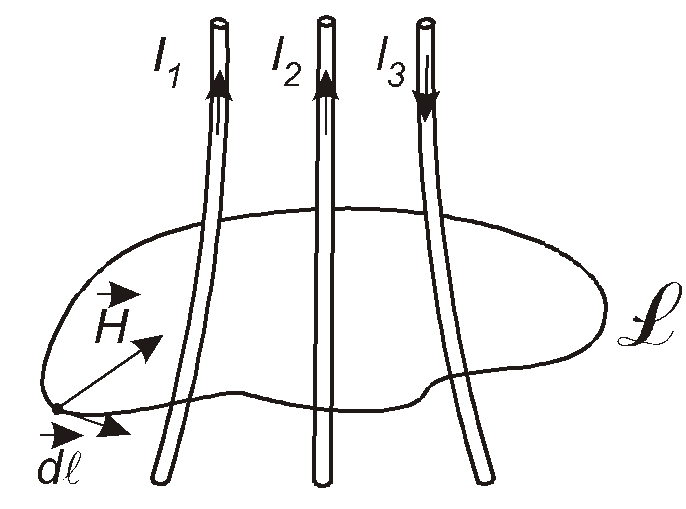
Рис. 3.6

Сума в правій частині співвідношення (3.3) є повним струмом.Додатний напрям кожного струмуI_kзв’язаний з проекцією векторана напрямза правилом гвинта з правою різзю. Тому для ситуації, зображеної на рис.3.6, маємо

.

Розглянемо як окремий випадок котушку індуктивності, яка має Wвитків (на рис. 3.7 схематично зображено три витки). Тут контурLохоплюєWвитків, у кожному з яких тече один і той самий струмI.

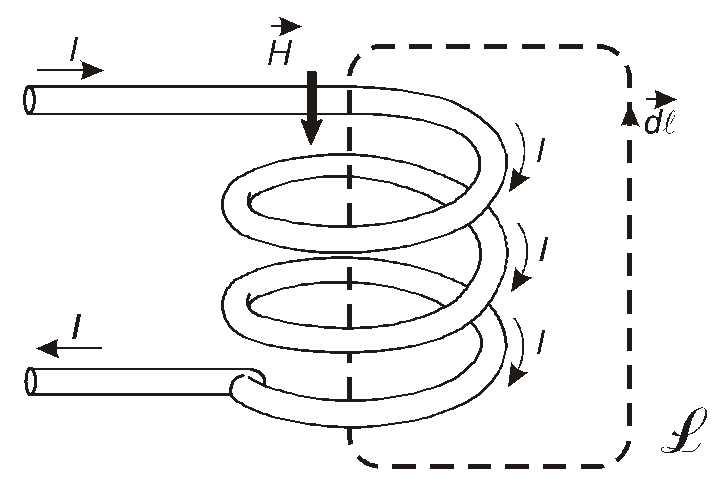
Рис. 3.7

Тому в даному випадку права частина співвідношення (3.3) набуває такого вигляду:

.

Скалярну величину Fназваномагніторушійною силою (МРС), яку розвиває котушка. Одиницею вимірюванняМРСє ампери.

3.5. Другий закон Кірхгофа та закон Ома для магнітних кіл. Аналогія між магнітним і електричним колами

Розглянемо конструкцію з феромагнітного матеріалу, проекцію якої на площину креслення зображено на рис. 3.8. Ця конструкція має певний розмір у напрямку, перпендикулярному площині креслення. Форма перерізу не є суттєвою для подальшого розгляду, але для конкретності умовимося вважати її прямокутною, причому площа перерізу на ділянці 6–1 становить S₁, а на ділянці 1-2-3-4-5-6 вона становитьS₂. На ділянку 6-1 намотано котушку з кількістю витківW; крізь цю котушку протікає постійний струм силоюI.

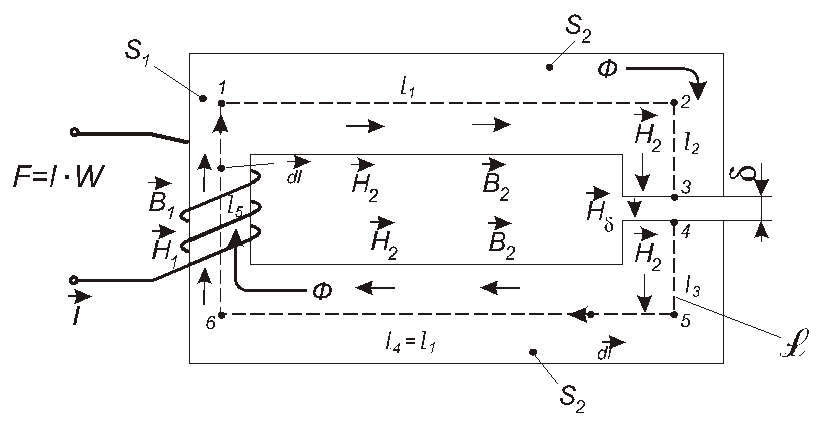
Рис. 3.8

При протіканні струму Iкотушка створює в даному магнітному колі магнітний потік величиноюФ¹.

Це так званий основний магнітний потік. Ту частину магнітного потоку, яка протікає поза феромагнетиком (так званий магнітний потік розсіювання), вважатимемо знехтувано малою. Тобто магнітний потік у розглянутому випадку тече тільки у феромагнітних стрижнях, які утворюють магнітопровід (осердя).

Будемо вимірювати довжини таділянок конструкції вздовж осі магнітопроводу, яка, до того ж, наближено збігається із середньою лінією магнітного поля (це наближення тим точніше, чим поперечні розміри стрижнів менше її довжин). Нехай довжиназазору набагато менша за сумарну довжину стрижнів, завдяки чому розсіюванням потоку із зазору можна знехтувати. Тому величинуФпотоку вважатимемооднаковоюв будь-якому перерізі даного магнітного кола, включно із зазором. Однак величинаВіндукції на різних ділянках кола єрізною, в залежності від площі перерізу:

,і = 1,2. (3.4)

Оскільки напруженість Нзалежить від індукціїВта магнітної проникності(3.4), то різними є і величиниН₁,Н₂таН_.

Запишемо закон повного струму для контуру, який збігається із середньою силовою лінією, враховуючи, що в будь-якій точці нашого магнітного кола вектори тапрактично збігаються за напрямком, звідки маємо=Hd. Тому

.

Відомо, що Н_і=В_і / (_і₀), і=1,2;

де _і–відносна магнітна проникність матеріалу на ділянці з площею перерізуS_і. Для феромагнетиків магнітна проникність залежить від величиниНнапруженості поля.

Тоді отримаємо, що

.

Підставивши сюди співвідношення (3.4), знайдемо, що

або

. (3.5)

Тут

, (3.6)

де – довжина ділянки магнітного кола;

 –відносна магнітна проникність цієї ділянки;

S– площа перерізу цієї ділянки.

Параметр R_Mназиваютьмагнітним опором. Проводячи аналогію між другим законом Кірхгофа для електричних кіл, у виразі (3.5) маємо МРСF– аналог ЕРС Е, магнітний потікФ– аналог струмуI, магнітний опірR_M–аналог електричного опоруR(звичайно, що розмірністюR_Mне є оми).

Величину

за аналогією називають падінням магнітної напруги (одиниця її вимірювання – ампери). Цей вираз є математичним формулювання закону Ома для магнітних кіл. Тоді вираз (3.5) означає, що в замкненому контурі магнітного кола величина МРС дорівнює сумі (можна довести, що ця сума –алгебраїчна) падінь магнітної напруги вздовж цього контуру. Це – другий закон Кірхгофа для магнітних кіл.

Наявність аналогії між електричним і магнітним колами дозволяє звести розрахунок магнітного кола до розрахунку електричного кола, яке є аналогом, і застосувати відомі методи розрахунку електричних кіл.