2.5. Розрахунок кола з одиночним нелінійним резистором методом еквівалентного генератора

Складне електричне коло, яке містить джерела електричної енергії та один-єдиний нелінійний резистор, можна розрахувати й методом еквівалентного генератора. Для цього цей нелінійний резистор слід виділити як навантаження, а решту кола слід уявити у вигляді активного двополюсника (наприклад, за теоремою Тевенена). Таку заміну проілюстровано рис. 2.13.

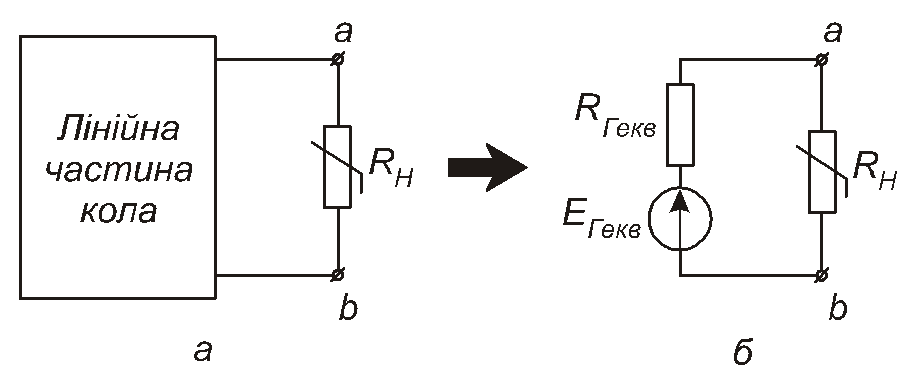
Рис. 2.13

Коло, що утворилося в результаті такої заміни (рис. 2.13,б), являє собою послідовне з’єднання лінійного резистора R_{г екв}та нелінійного резистораR_н. Розрахунок таких кіл вже розглянуто в підрозділі 2.4.1 (не забудьте прочитати зауваження в середині цього підрозділу).

2.6. Додаткова інформація щодо методів розрахунку нелінійних резистивних кіл

Базовані на графічних побудуваннях методом розрахунку більш складних кіл, аніж такі, що розглянуті в даному розділі, наведені в низці поширених підручників, наприклад, в [1, 2, 6].

Якщо нелінійне коло описане виключно рівняннями, складеними на базі законів Кірхгофа, то, як зазначено в підручнику [5], точне аналітичне розв’язання такої системи рівнянь (яка містить принаймні одне нелінійне рівняння) можливе лише у виключних випадках. Тому подібну систему рівнянь розв’язують наближеними числовими, графічними або графо-аналітичними методами.

Лекція 9

3. Магнітні кола при постійних магніторушійних силах

3.1. Магнітне поле та основні величини, які його характеризують

Як відомо з курсу фізики, два провідники, в яких течуть струми, або провідник, в якому тече струм, та магніти, або два магніти взаємодіють між собою (притягуються або відштовхуються). Ця взаємодія здійснюється крізь особливе середовище – магнітне поле. Це поле виникає як результат руху електричних зарядів, тобто внаслідок протікання деякого струму.

Магнітне поле виявляють за його дією на провідники, в яких тече струм (тобто рухаються електричні заряди) та на намагнічені тіла. Силу , що діє з боку магнітного поля на заряд величиноюq, який рухається із швидкістю, розраховують як

.

Вектор називаютьіндукцією магнітного поля. Його величина характеризує ступінь силової дії поля на заряд, що рухається, в будь-якій точці пронизаного полем простору, заповненого певною речовиною. Індукцію у вакуумі позначимо як. У фізиці вводять векторну величину

,

яку названо напруженістю магнітного поля. Одиницею вимірювання напруженості є ампер, поділений на метр (А/м). Величину₀називаютьмагнітною проникністю вакууму, її числове значення дорівнює410^-7Гн/м, деГн– генрі (відома з курсу фізики одиниця вимірювання індуктивності).

Індукцію магнітного поля, створюваного певним джерелом поля в певній речовині, розраховують через індукціюполя, створюваного тим же джерелом у вакуумі, як

(3.1)

Тут –відносна магнітна проникність даної речовини; вона показує, в скільки разів індукція в цій речовині відрізняється від індукції у вакуумі. Це безрозмірна величина . Величину індукціївимірюють у теслах(Тл), при цьому1 Тл=1.

Величини тане завжди збігаються одна з одною за напрямком, як це може здатися з огляду на формулу (3.1). Існують так звані анізотропні в магнітному відношенні матеріали, в яких величиназалежить від напрямку вектора. У даному курсі ми, однак, не будемо розглядати цей випадок.

Розглянемо область простору, пронизану однорідним магнітним полем, тобто таким полем, вектор напруженості якого має один і той самий напрямок та одну і ту саму довжину в будь-якій точці розгляданої області. Виділимо в цій області поверхнюSта розіб’ємо її на елементарні площадки, кожна з яких має площуdS, яка прямує до нуля (рис. 3.1). Задамо вектор зовнішньої нормалі, який має одиничну довжину і спрямований перпендикулярно даній площадціdS.

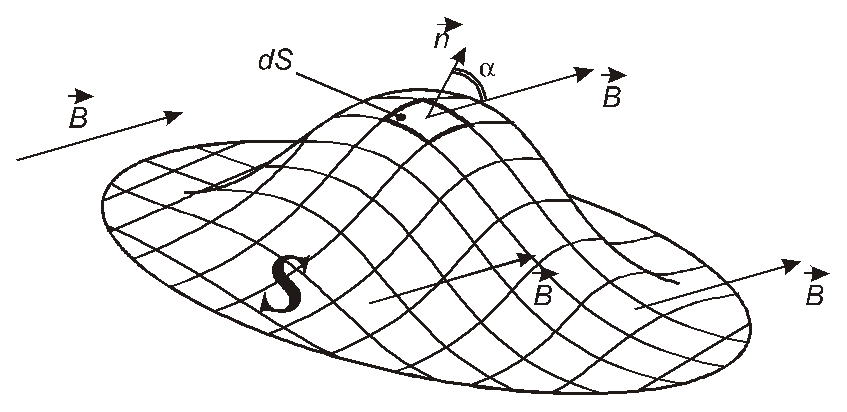
Рис. 3.1

У цих позначеннях потік Фвектораіндукції магнітного поля крізь поверхнюSрозраховують як інтеграл по цій поверхні:

, (3.2)

де .

Для окремої площадки маємо елементарний потік

,

де –кут між векторамита(рис. 3.1).

Якщо поверхня Sбуде плоскою, то кут  на ній всюди один і той самий. Оскільки в однорідному полі величинаВтеж одна і та сама в будь-якій точці поверхні, то з (3.2) маємо, що

,

де S– площа поверхніS.

Якщо ж вектор є ще й перпендикулярним доS, то отримаємо, що

Ф=ВS.

Одиницею вимірювання магнітного потоку є вебер (Вб), причому1Вб=1 Тлм².