2.2. Статичний та диференціальний опори

Нарівні з ВАХ нелінійний елемент може бути охарактеризований сукупністю числових значень його так званих статичних та диференціальних опорів при всіх числових значеннях напруги на цьому елементі.

Статичний опір R_ст – це відношення постійної напруги на нелінійному елементі до величини викликаного цією напругою постійного струму крізь нелінійний елемент.

Наприклад, у точці адеякої ВАХ, зображеної на рис. 2.4, величина статичного опору дорівнюватиме

R_ст =U_a / I_a

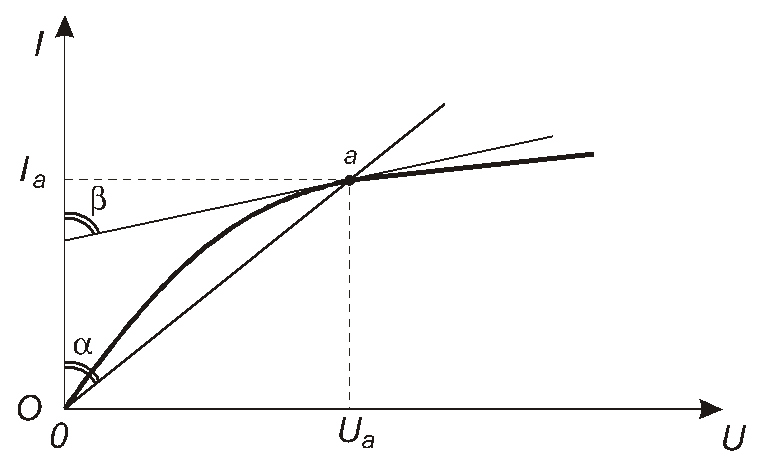
Рис. 2.4

або

,

де m_Uтаm_I– масштаби графічного побудування по осяхUтаI(відповідною розмірністюта).

При переході від однієї точки ВАХ до іншої величина R_стзмінюється, причому ця величина завжди більша за нуль.

Диференціальний опір R_д – це границя відношення зростання напруги на нелінійному елементі до зростання струму в ньому, коли це зростання прямує до нуля. При цьому зміни напруги або струму повинні відбуватися нескінченно повільно (дане зауваження відноситься перш за все до експериментального визначення величиниR_д).

Отже, диференціальний опір у будь-якій точці ВАХ дорівнює похідній , обчисленій у даній точці. Тому можна також вважати, що

,

де – кут нахилу дотичної до кривої ВАХ у розгляданій точці (наприклад, точкаана рис. 2.4).

Зображена на рис. 2.4 ВАХ є монотонно зростаючою, тому в будь-якій її точці величина R_дбільша за нуль. Але існують нелінійні елементи (наприклад – тунельний діод), ВАХ яких містить спадаючу ділянку, як це зображено на рис. 2.5.

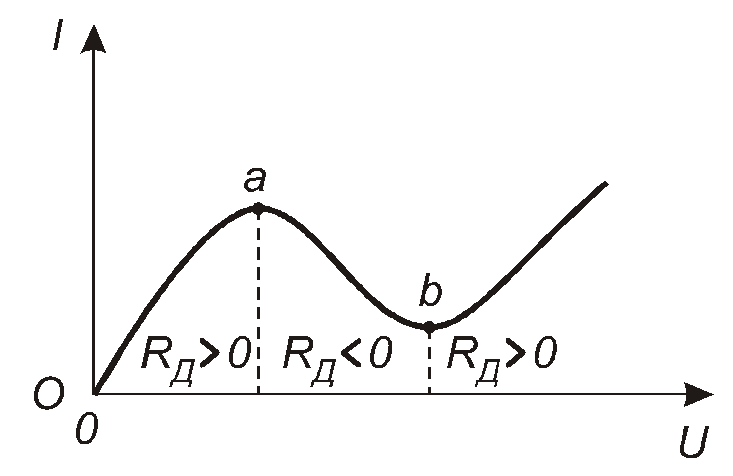
Рис. 2.5

Тут на ділянці авпризростаннінапругизменшується струм, тому в будь-якій точці цієї ділянки величинаєвід’ємною,отже – від’ємним тут є й диференціальний опір.

2.3. Закономірності, загальні для лінійних та нелінійних кіл постійного струму

Для нелінійних кіл зберігає свою чинність закон Ома, але тепер він відноситься тільки до статичних опорів, тобто записується як U=R_стI. Оскільки у нелінійного елементавеличина R_ст є різною в різних точках ВАХ, то не можна, обчислившиR_стпри одному деякому значенніU(абоI), користуватись цим опором при будь-якому іншому значенніU(абоI).

Обидва закони Кірхгофа також зберігають свою чинність для нелінійних кіл постійного струму. Чинним залишається ібаланс потужностей.

Однакдля нелінійних кіл не є справедливим принцип накладання, тобто для них результат сумісної дії кількох джерел не дорівнює сумі результатів дії кожного з цих джерел окремо. Тому для розрахунку нелінійних кіл не можна використовувати метод накладання та інші методи, які базуються на принципі накладання, наприклад, метод контурних струмів та метод пропорційних величин.

2.4. Прості нелінійні кола постійного струму

2.4.1. Коло з послідовним з’єднанням нелінійних резисторів

Розглянемо нелінійне коло, схема якого зображена на рис. 2.6. Нехай є відомими величина ЕРС та ВАХ обох нелінійних резисторів (рис. 2.7). Треба знайти струм I₀в колі.

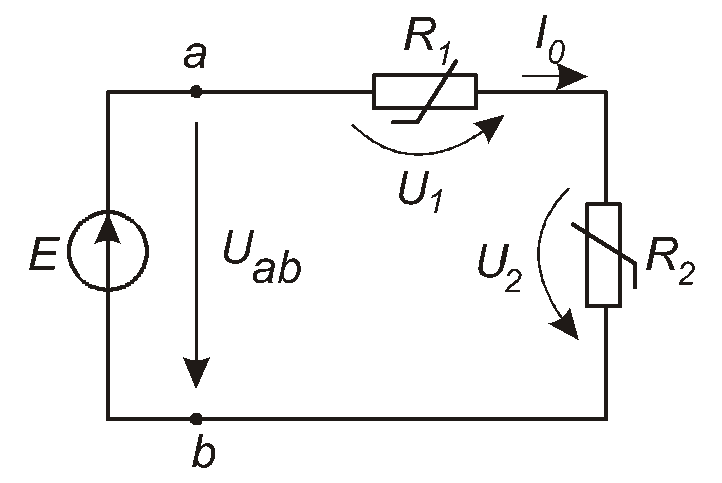
Рис. 2.6

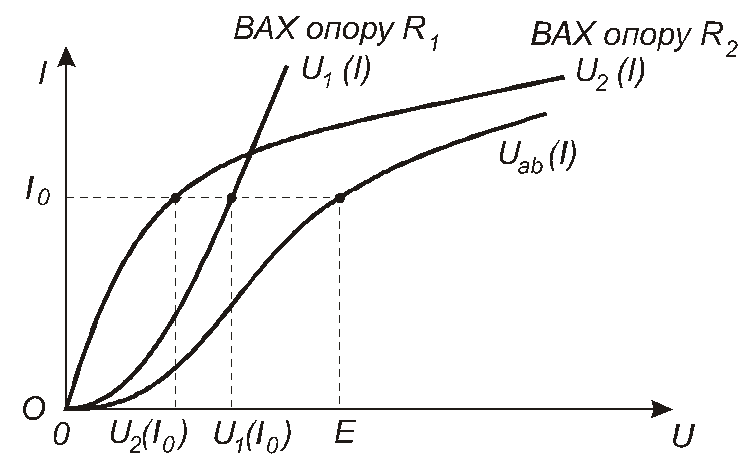
Рис. 2.7

По-перше, зазначимо, що при шуканому струмові I₀повинна використовуватись рівність

. (2.1)

По-друге, зазначимо, що при будь-якому струмові I, згідно з другим законом Кірхгофа, виконується рівність

. (2.2)

Оскільки U₁(I)таU₂(I)–це ВАХ окремих резисторів, тоU_ав(I)можна вважати ВАХ деякого нелінійного резистора, еквівалентного цим двом послідовно з’єднаним резисторам. Побудуємо графікU₁(I), підсумовуючи, згідно з рівністю (2.2), величини напругиU₁таU₂при кожному значенні струмуI, тобто додаючи графікиU₁(I)таU₂(I)за напругою. А тепер, згідно з рівністю (2.1), з цього сумарного графіка знаходимо величину струмуI₀, при якійU_ав = Е. Для цього відкладаємо на осі напруг величинуЕта проводимо крізь цю точку вертикаль до перетину з графікомU_ав(I). Величина струму, що відповідає точці перетину, є величиною шуканого струмуI₀.

Зауваження.Якщо один з двох резисторів у колі (рис.2.6) лінійний з відомим опоромR, то перед розв’язанням задачі слід побудувати його ВАХ як графік функціїU=IR.

Корисне узагальнення. При послідовному з’єднанні кількох нелінійних резисторів графік ВАХ еквівалентного нелінійного резистора утворюють шляхом додавання за напругою графіків усіх окремих резисторів, які входять у це з’єднання.

Можна знайти величину струму I₀, не будуючи графіка ВАХ еквівалентного опору. Запишемо для кола, схема якого наведена на рис.2.6, рівність за другим законом Кірхгофа:

.

Звідси

. (2.3)

Побудуємо допоміжний графік функції (рис. 2.8). Рівність (2.3) виконується в точці перетину графікаU_д(I)та графікаU₂(I). Величина струму, що відповідає цій точці, є величиною шуканого струмуI₀.

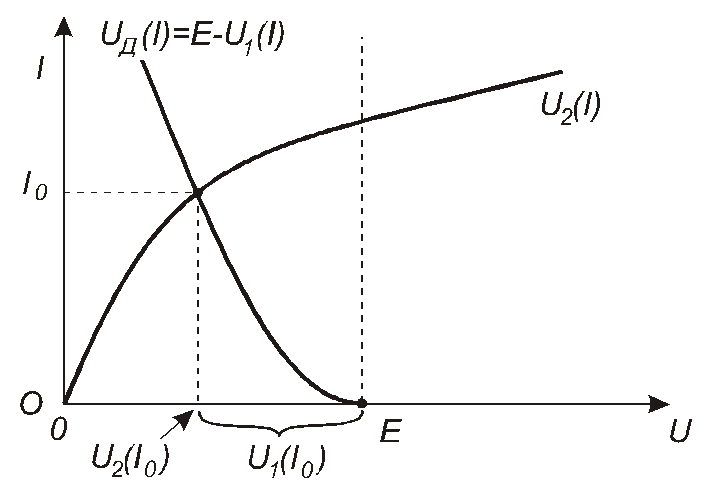
Рис. 2.8

Зазначимо, що графік U_д(I)– це графікU₁(I),який перенесено в точкуЕта дзеркально відображено відносно вертикалі, проведеної крізь цю точку. Тому метод, проілюстрований рис.2.8, інколи називаютьметодом дзеркального відображення.