П.5. Множественная корреляция.

На практике часто приходится исследовать статистические связи между тремя и большим числом признаков.

Пусть результаты измерения признаков X, Y, Z у объектов некоторой статистической совокупности представлены в следующей таблице:

X	Y	Z	Частота n
x1	y1	z1	n1
x2	y2	z2	n2
xi	yi	zi	ni
xn	yn	zn	nn

Если предположить, что зависимость признака Z от признаков X и Y имеет вид , а отклонения табличных значенийZ от соответствующих значений приведённой функции носят случайный характер, то коэффициенты α, β, γ могут быть определены по методу наименьших квадратов, который для их определения баёт следующую систему линейных алгебраических уравнений:

Решая эту систему, находим, что

, ,,

где – коэффициент корреляции междуX и Y и т.д.; 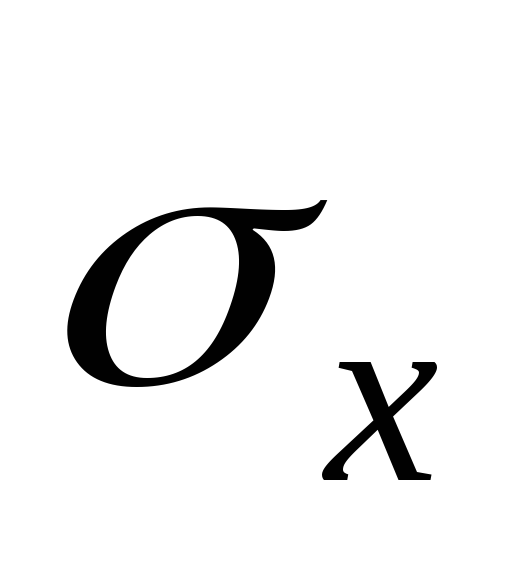,,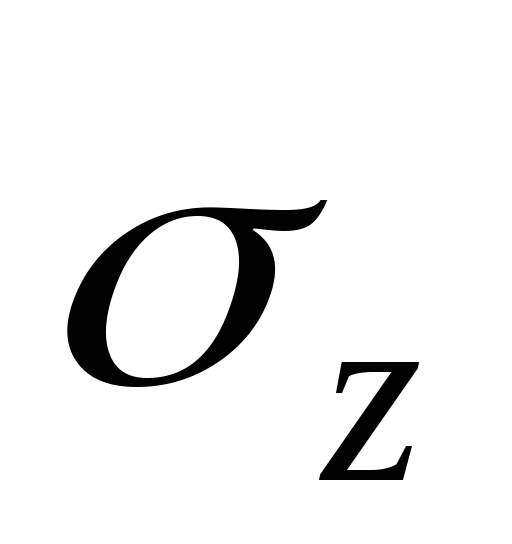- средние квадратические отклонения признаковX, Y, Z; а ,,– их выборочные средние значения.

За меру тесноты линейной связи между Z и X и Y принимают совокупный коэффициент корреляции:

.

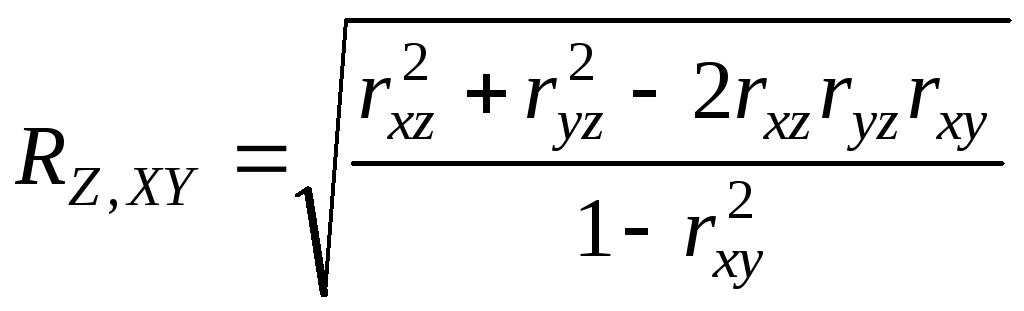Совокупный коэффициент корреляции обладает следующими свойствами:

1) ;

2) если , то между признакомZ и признаками X и Y отсутствует линейная зависимость;

3) если , тоZ находится в линейной функциональной зависимости от X и Y ().

Для установления влияния признака X (или признака Y) на изменение Z пользуются частным коэффициентом корреляции:

,

(аналогично определяется и ). Свойства частных коэффициентов корреляции такие же, как и свойства коэффициентов линейной корреляции.

9
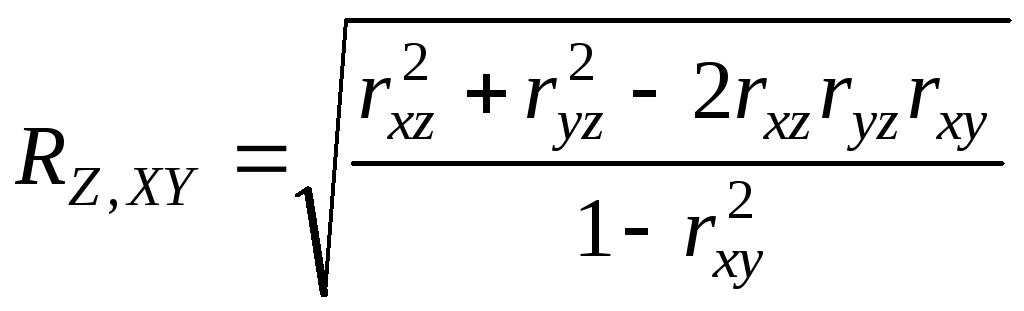