Тема 6. Средняя энергия молекул

Каждая молекула характеризуется числом степеней свободы (i) – это количество независимых движений, которые может совершать молекула:

1. одноатомная молекула может совершать три поступательных движения вдоль направлений координатных осей: i=3(пост);

2. двухатомная молекула с жесткими связями может совершать три поступательных и два вращательных движения: i=3(пост)+ 2 (вращ)=5;

3. трехатомная молекула и более может совершать три поступательных и три вращательных движения: i=3(пост)+ 3 (вращ)=6;

4. если связи между атомами внутри молекулы не жесткие, она совершает колебательные движения – добавляются колебательные степени свободы.

Полное число степеней свободы молекулы:

.

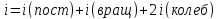Например, молекула Н₂ двухатомная с жесткими связями – число степеней свободы равно 5.

Закон равнораспределения энергии по степеням свободы молекулы: на каждую поступательную и вращательную степень свободы молекулы приходится одинаковая порция энергии , а на каждую колебательную степень свободы двойная порция энергии гдеk – постоянная Больцмана, Т – температура по шкале Кельвина.

Тогда полная энергия молекулы, равна: ,

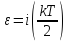где i – число степеней свободы молекулы.

Энергия одного моля газа, равна: , гдеR – универсальная газовая постоянная.

Энергия произвольной массы газа, равна: U.

Молярная теплоёмкость газа при постоянном объёме: .

Молярная теплоёмкость газа при постоянном давлении: .

Пример 6.1. Средняя кинетическая энергия молекул газа при температуре Т зависит от их структуры, что связано с возможностью различных видов движения атомов в молекуле. При условии, что имеют место только поступательное и вращательное движение, средняя энергия молекул азота (N₂) равна:

 (7/2)kT  (5/2)kT  (3/2)kT  (1/2)kT.

Решение 6.2. молекула азота двухатомная, число степеней свободы равно 5, следовательно, энергия молекулы равна .

Пример 6.3. При комнатной температуре отношение С_P/С_V при постоянном давлении и объеме равно 8/6 для:

гелия воздуха водяного пара кислорода

Решение: чтобы решить это задание нужно найти число степеней свободы молекулы с приведенным отношением теплоемкостей:

,

выведем формулу для расчета i: ,,

посчитаем .

Число степеней свободы молекулы равно 6 – это трехатомная молекула, из вариантов ответов – это водяной пар Н₂О.

Тема 7. Первое начало термодинамики. Работа при изопроцессах

первый закон термодинамики: в замкнутой макроскопической системе работа, произведенная над системой и количество теплоты, переданное системе, идут на изменение внутренней энергии системы:

.

Применение первого закона термодинамики:

1) изотермический процесс – все тепло, поступающее в систему идет на совершение работы: ,,.

2) изохорный процесс – изменение внутренней энергии системы происходит за счет передачи тепла:

, ,

3)изобарный процесс: ,.

Из последнего выражения видно, что теплоемкость газа при изобарном процессе больше теплоемкости при изохорном процессе, что раньше мы записали в виде соотношения Майера.

Величины молярных теплоемкостей вещества могут быть рассчитаны, если известно число степеней свободы молекул вещества:

Отношение теплоемкостей С_р и С_v – постоянная адиабаты: .

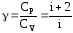При понижении температуры газа степени свободы молекулы «замораживаются» и ее теплоемкость уменьшается (см. рис. Для кислорода).

1. адиабатный процесс – процесс происходит без теплообмена с окружающей средой:

, ,

, ,.

5)циклические процессы – это круговые процессы: U=0, А= Q.

Пример 7.1. Идеальному газу сообщается одинаковое количество теплоты при изохорном (1), изобарном (2) и изотермическом (3) процессах. Для совершаемых газом работ справедливы соотношения:

   

_{Решение:} применение первого закона термодинамики дает, что при изохорном процессе работа равна нулю, при изобарном разности полученного тепла и изменения внутренней энергии, а при изотермическом – все тепло пошло на совершение работы, следовательно: .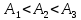

Пример 7.2. Диаграмма циклического процесса идеального одноатомного газа представлена на рисунке. Чему равно отношение работы при нагревании газа к работе при охлаждении?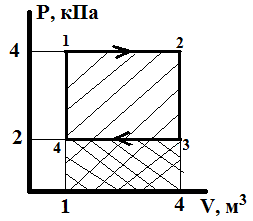

Решение: работа совершается только при изменении объема газа, т.е. на участках (1,2) и (3,4). Это изобарные процессы, при которых объем пропорционален температуре газа ( ), следовательно участок (1,2) – нагревание, а (3,4) – охлаждение.

Работа газа равна площади фигуры под графиком зависимости давления от объема. Работа при нагревании – площадь прямоугольника (141234):

А_н = 4(кПа)  4 (м³) =40004=16000 Дж.

Работа при охлаждении – площадь прямоугольника (1434):

А_о= 2(кПа)  4 (м³) =20004=8000 Дж.

Тогда отношение работ равно: А_н/А_о = 16000/8000 = 2. Ответ: 2.

Пример 7.3. Работа, совершаемая идеальным газом при его изобарном расширении, численно равна заштрихованной площади, показанной на рисунке …

Решение: чтобы дать ответ необходимо определить на каком графике изображен изобарный процесс (при постоянном давлении) – на рисунке 2. (Эти же рис. можно использовать в задании о работе при изотермическом процессе – ответ рис. 5., при круговом процессе – ответ рис. 1.)

Пример 7.4. При изотермическом расширении 0,5 моля газа при температуре 200 К объем увеличился в е раз ( е=2,7). Чему равна работа газа (в Дж)?

Решение: работа при изотермическом процессе определяется по формуле:

где m/=0,5 моль; V₂/V₁=e; ln(е)=1; R=8,31Дж/мольК; T=200К

Ответ:

Пример 7.5. Одному молю двухатомного газа было передано 5155 Дж теплоты, при этом газ совершил работу, равную 1000 Дж. Насколько повысилась его температура? Ответ: на 200 K.

Решение: по условию задачи дано Q=5155 Дж; A’=1000Дж;

i = 5(число степеней свободы двухатомной молекулы);  = 1 моль.

Первое начало термодинамики:

, где ,

Пример 7.6. Одноатомному идеальному газу в результате изобарического процесса подведено количество теплоты Q. На увеличение внутренней энергии газа расходуется часть теплоты U/Q, равная: 0,7 0,6 1,7 1,4

Решение: число степеней свободы молекул одноатомного газа равно трем (i=3). Запишем формулы для изобарного процесса:

Пример 7.7. Молярные теплоемкости гелия в процессах 1-2 и 1-3 равны С₁ и С₂ соответственно. Тогда С1 / С2 составляет…

 3/5  7/5  5/7  5/3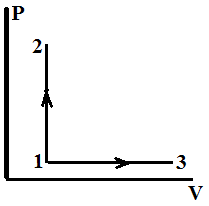

Решение: процесс 1-2 изохорный, а 1-3 изобарный.

_{Гелий одноатомный газ – число степеней свободы молекулы равно i=3, следовательно,}

Пример 7.8. Состояние идеального газа определяется значениями параметров:T₀, P₀, V₀, где Т – термодинамическая температура, Р – давление, V – объем газа. Определенное количество газа перевели из состояния (3Р₀, V₀) в состояние (Р₀, 2V₀). При этом его внутренняя энергия… увеличилась  уменьшилась  не изменилась

Решение: мерой внутренней энергии газа (и любого вещества) служит его температура. Если температура изменяется – так же изменяется внутренняя энергия, если температура неизменна – значит и внутренняя энергия не меняется. Т.о. чтобы решить это задание нам необходимо определить как меняеися температура газа.

Состояние газа характеризует уравнение Клапейрона-Менделеева:

, следовательно, температура пропорциональна произведению давления и объема ().

По условиям задачи: ,,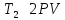 следовательно.

Пример 7.9. В цилиндре при сжатии постоянной массы воздуха давление возрастает в 3 раза. Если температура газа увеличилась в 2 раза, то отношение объемов до и после сжатия равно…

 3/2  6  1/6  2/3

Решение: по условию задачи Р₂ = 3Р₁, Т₂ = 2Т₁. Определим объемы газа из уравнения Клапейрона-Менделеева:

.

Пример 7.10. Если U – изменение внутренней энергии идеального газа, А – работа газа, Q – количество теплоты, сообщаемое газу, то для изохорного охлаждения газа справедливы соотношения…

 Q  0; A  0; U = 0

 Q = 0; A  0; U  0

 Q  0; A = 0; U  0

 Q = 0; A  0; U  0

Решение: изохорный процесс протекает при постоянном объеме, значит, работа равна нулю (А=0). При охлаждении температура и внутренняя энергия уменьшаются (U  0). Газ не совершает работу, охлаждается, значит, он отдает тепло (Q  0).

(если бы происходило адиабатное сжатие газа – тепло не поступает Q = 0; сжатие A  0; при сжатии газ нагревается U  0 – ответ вторая строчка). Самостоятельно рассмотрите адиабатическое расширение, изотермическое сжатие, изобарное охлаждение, изобарное нагревание.