2. Вычисление площадей

Площадь криволинейной трапеции прилежащей к оси(рис.1):

Дифференциал переменной площади равен

Если кривая, заданная уравнением и, то

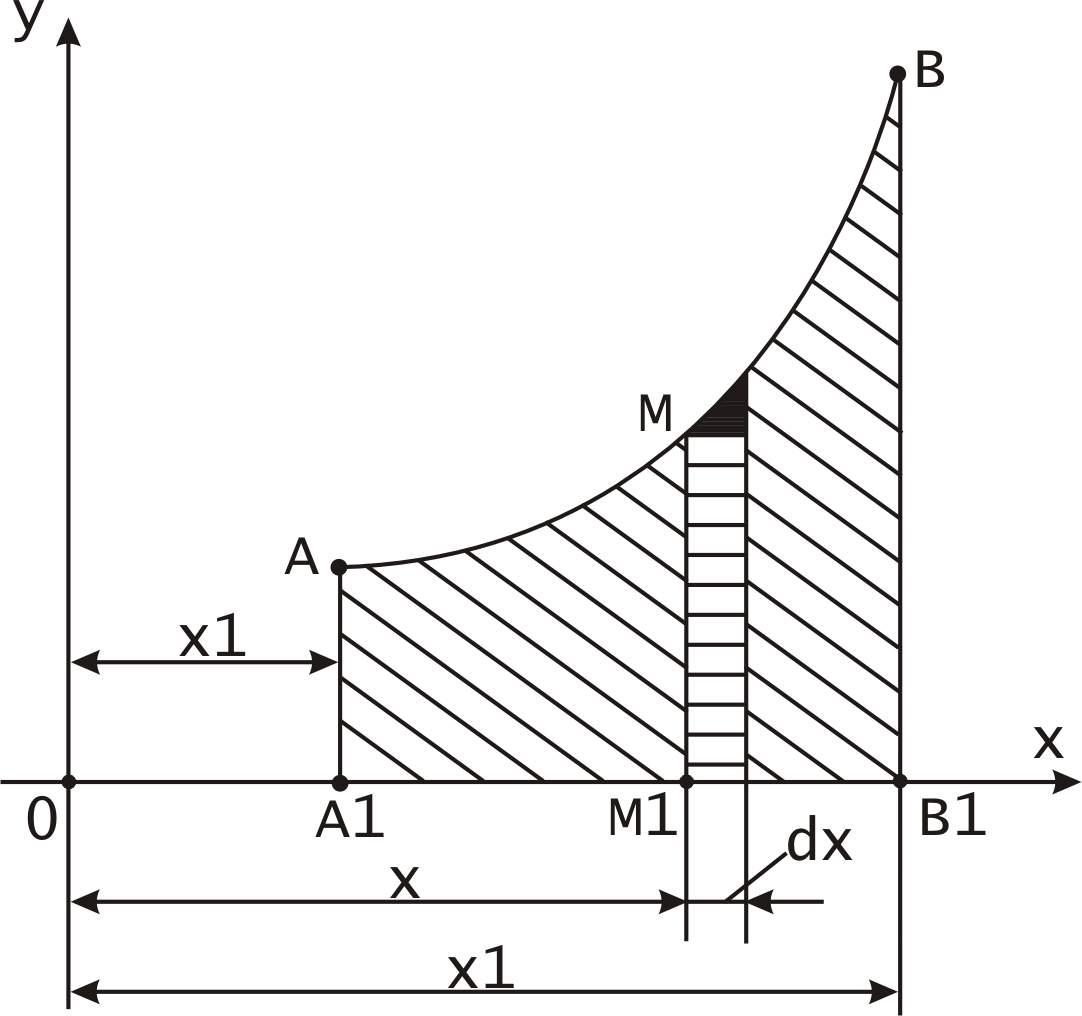
Рис.1 Рис.2

Площадь криволинейной трапеции, прилежащей к оси :

. (2.2)

Дифференциал переменной площади

Площадь сектора (рис.2) кривой, заданной вполярных координатах:

Дифференциал переменной площади

3. ОБЪЕМ ТЕЛА ВРАЩЕНИЯ

Объем тела, образованного вращением вокруг оси криволинейной трапеции(рис.3), где- дуга кривой, определяется формулой

(3.1)

Дифференциал переменного объема

Объем тела, образованного вращением круга вокруг осикриволинейной трапеции, прилежащей к оси, определяется формулой

(3.2)

Дифференциал переменного объема

4. ДЛИННА ДУГИ ПЛОСКОЙ КРИВОЙ

Длинна дуги кривой

(4.1)

Дифференциал дуги

Длинна дуги кривой

(4.2)

Длинна дуги кривой

(4.3)

5. ПЛОЩАДЬ ПОВЕРХНОСТИ ВРАЩЕНИЯ

Площадь поверхности, образованной вращение вокруг оси дугикривой

где

Площадь поверхности, образованной вращением вокруг оси дугикривой

где

6. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ

Определения.

1. Интегралом называется, если этот предел существует и конечен. Аналогично определяются интегралы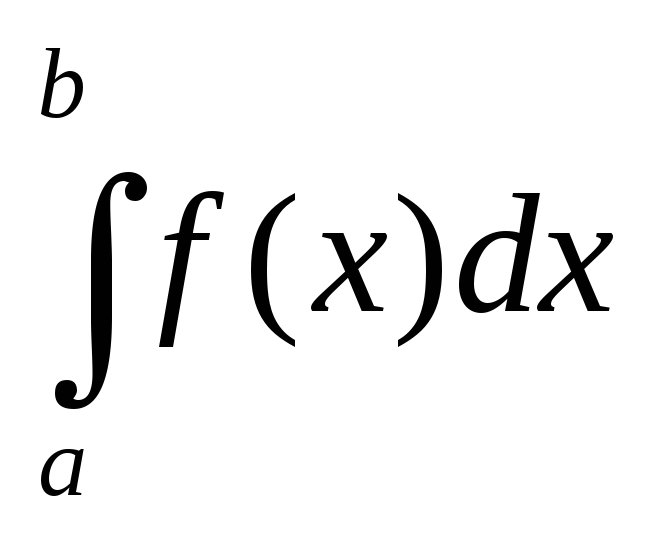и

2. Если непрерывна для всех значений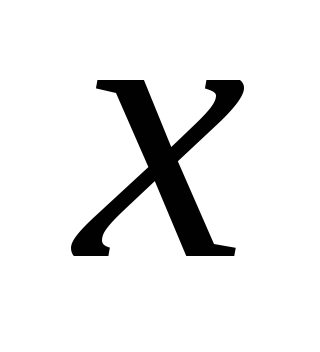отрезка, кроме точки, в которойимеет разрывIIрода, то интегралом отв пределах отдоназывается суммой

,

если существуют и конечны.

Интегралы с бесконечными пределами и интегралы отразрывных (неограниченных) функций называютнесобственными.

Если приведенные выше пределы конечны, то говоря, несобственные интегралы сходятся, если нет, - торасходятся.

Сходимость несобственного интеграла часто устанавливается методом сравнения:

Если при исходятся, то сходятся и

Аналогичный признак сходимости можно указать и для интеграла от разрывной функции.

7. Среднее значение функции

Теорема о среднем. Если на отрезке функциянепрерывна, то между пределами интеграланайдется такое, при котором

(7.1)

Значение функции

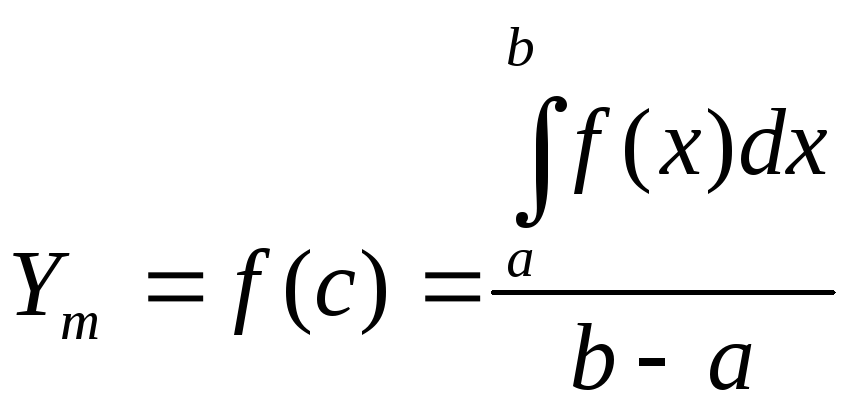(7.2)

называется средним значением функциина отрезке.

8. ФОРМУЛА ТРАПЕЦИЙ И ФОРМУЛА СИМПСОНА

Формула трапеций:

(8.1)

где - равностоящие ординаты кривойна отрезке. Погрешность формулы (I):

, (8.1)

Параболическая формула Симпсона для двух полос:

(8.II)

где

Формула Симпсона для полос:

, (8.III)

где Погрешность формул (II) и (III):

(8.2)

т.е. формула (III) является точной для парабол второй и третей степеней:

.

НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

Задачи

Найти интегралы:

1.;2.;3. ;4.;

5.;6.;7.;

8.;9.;10.;11.;

12.;13.;14.;15.;

16.;17.;18.;19.;

20.;21.;22.;

23.;24.;

Выполнить интегрирование, не прибегая к методу неопределенных коэффициентов:

25.;26.;27.;28.;

Найти интегралы:

29.;30.;31.;32.;

33.;34.;35.;36.;

37.;38.; 39.;40.;

41.;42.;43.;44..

ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

Задачи

Вычислить:

1. ; 2.; 3. ; 4. ; 5.;

Вычислить площадь, ограниченную линиями:

6. отдо.

7.Общей части эллипсови(перейти к полярным координатам).

8.и.

9..

10.между смежными наибольшим и наименьшим радиус – векторами.

Определить объем тела, образованного вращением фигуры, ограниченной линиями:

11.вокруг прямой.

Указание. .

12.Одной арки циклоидывокруг оси.

13.вокруг оси.

14.вокруг оси.

15.,вокруг оси.

Определить длину кривой дуги:

16. отдо.

17., отсеченной прямой

18.между точками пересечения с осью.

19., отсеченной прямой.

20.Гибкая нить подвешена в точкахи, находящихся на одной высоте на расстоянии, и имеет стрелу пробега. Считая форму нити параболой, показать, что длина нитипри достаточно малом.

Указание. Применить приближенную формулу .

Определить площадь поверхности, образованной вращением вокруг оси :

21.Дуги кривой, отсеченной прямой.

22.Всей кривой.

23.Дуги кривоймежду точками пересечения с осями координат.

24.Дуги кривойотдо.

25.Определить площадь поверхности, образованной поверхностью вращения кривой:

вокруг оси.

26.Вычислить площадь, заключенную между кривойс осями координат.

27.Найти объем тела, образованного вращением вокруг осиплощади бесконечной длинны, заключенной между линиями:

28.Определить объем тела, образованного вращением кривойвокруг ее асимптоты.

Вычислить интегралы:

29.;30.;31.;32.

Указание. В примере 32 при нахождении применить правило Лопиталя.

Определить среднее значение функции:

33.на отрезке;

34.на отрезке;

35.на отрезке;

36.на отрезке;

37.на отрезке

38.Вычислитьпо общей формуле Симпсона (III) (при) и оценить погрешность, полагая в формуле (2) приближенно

39.рассматривая площадь части круга, ограниченного кривой, показать, что

; найти, вычисляя интеграл по формуле Симпсона (при).

40.Вычислить по формуле Симпсона (III) длину дуги полуволны синусоиды, разбив отрезокна шесть равных частей.

41.Вычислить приближенно, применив к интегралу формулу Симпсона (II).

42.Найти длину дуги эллипса, применив к интегралу, определяющему первую четверть всей дуги, формулу Симпсона (II).