6. Средние величины и показатели вариации Средние величины

Средняя величина – обобщающая характеристика совокупности однотипных явлений, показывающая типичный уровень признака, отнесенный на одну единицу совокупности, является показателем центра распределения исследуемой совокупности или показателем центральной тенденции.

Правила расчета средних

1. Совокупность, по которой рассчитывается средняя, должна быть достаточна, многочисленна (не менее трех единиц), чем больше совокупность, тем точнее расчет средней.

2. Единицы совокупности должны быть однородны как в качественном плане (при расчете среднего роста не должны попасть данные веса), так и в количественном (средний уровень жизни по стране является лишь описательной характеристикой, но не типической характеристикой, и в данном случае все население страны необходимо разбить на группы, которые отражают достаток, и рассчитывать групповые средние).

Общая формула степенной простой средней:

. (6.1)

Общая формула степенной взвешенной средней:

, (6.2)

где  степенная средняя;

индивидуальное значение для i-й единицы совокупности;

знак степени;

знак суммирования;

частота, с которой в совокупности появляется i-о значение варианты.

Средняя арифметическая простая:

. (6.3)

Средняя арифметическая взвешенная:

. (6.4)

Основные свойства средней арифметической

1. Средняя арифметическая постоянной величины равна этой постоянной.

2. Если каждую варианту 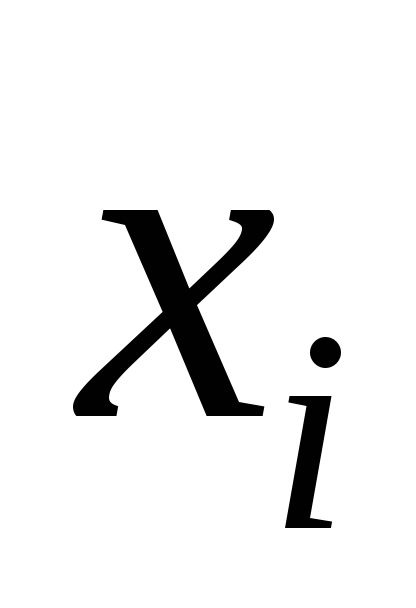увеличить или уменьшить на одно и то же постоянное число, то новая средняя увеличится или уменьшится на это же число.

3. Если каждую вариантуумножить или разделить на одно и то же постоянное число, то новая средняя увеличится или уменьшится во столько же раз.

4. Сумма всех отклонений вариантов от средней (как простой, так и взвешенной) всегда равна нулю:

и , (6.5)

5. Сумма всех квадратов отклонений вариантов от средней (как простой так и взвешенной) всегда меньше суммы квадратов отклонений от любой другой произвольной величины:

, (6.6)

6. Если все частоты разделить (умножить) на одно и то же постоянное число, средняя от этого не изменится.

7. Средняя многочлена равна многочлену средних:

. (6.7)

Средняя гармоническая применяется при обобщении обратных значениях изучаемого явления.

Прямые значения признака  такие значения, которые увеличиваются при увеличении определяющего показателя и характеризуемых ими явлений и уменьшаются при уменьшении.

Обратные значения признака  такие значения, которые увеличиваются при уменьшении определяющего показателя и характеризуемых ими явлений и уменьшаются при увеличении.

Средняя гармоническая простая:

, (6.8)

Средняя гармоническая взвешенная:

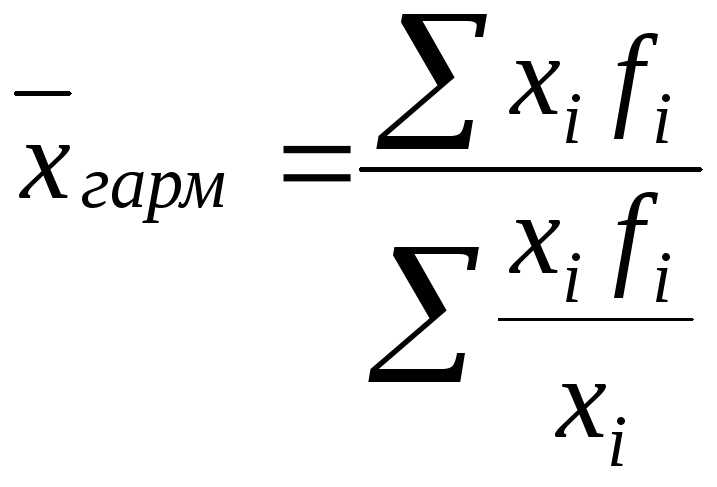, (6.9)

Средняя квадратическая простая:

, (6.10)

Средняя квадратическая взвешенная:

, (6.11)

Средняя кубическая простая:

, (6.12)

Средняя квадратическая взвешенная:

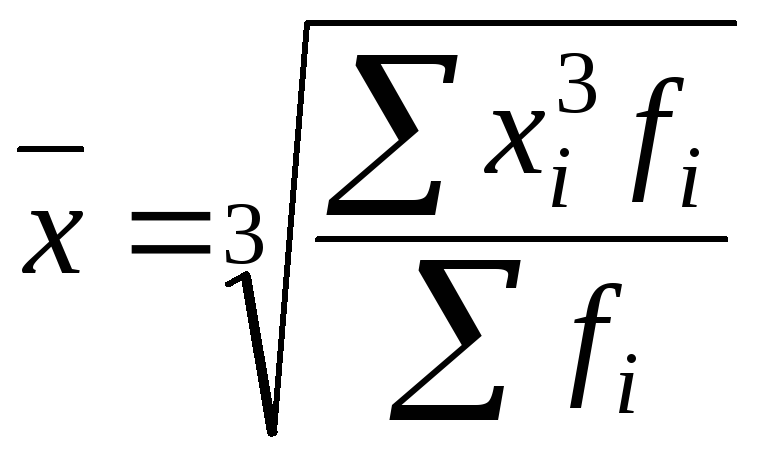. (6.13)