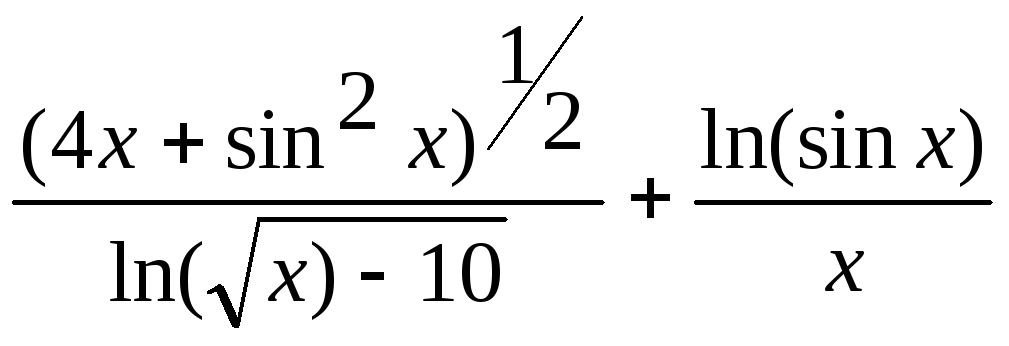D. Лабораторный практикум d.1 Лабораторная работа № 1
Тема: Линейные программы, выражения, встроенные функции.
Цель: Написание и отладка линейных программ вычисления значений выражений.
Прежде чем приступить к написанию и отладке программ, решающих задачу первой лабораторной работы, необходимо по конспектам лекций и учебникам ознакомиться со следующим материалом:
Общая структура программ на Паскале;
Разделы описаний Паскаль – программы; описание переменных;
Стандартные типы данных в Паскале;
Операторы ввода –вывода, присваивания;
Правила записей выражений, знаки арифметических операций, их приоритеты;
Встроенные функции Паскаля, типы их аргументов и результатов.
Только после уяснения материала можно приступать к выполнению работы. Вначале необходимо проанализировать условие поставленной задачи: если в ней отсутствуют какие – либо ограничения на значения исходных данных, то следует добиться, чтобы программа корректно работала при любых значениях исходных данных.
Для этого необходимо рассмотреть заданное выражение и выяснить, можно ли получить значение этого выражения для произвольных исходных данных, т.е. определить те значения исходных данных, при которых нельзя получить численные результаты. Далее на основе проведенного анализа составляют алгоритм (обычно – схему алгоритма).
После этого пишут программу на Паскале. В программе используют математические встроенные функции, к которым относятся:
abs (x) –х ln (x) – ln (x)
arctan (x) – arctg x sin (x) – sin x
cos (x) –
cos x sqr (x) - x
exp (x) –
e
sqrt
(x) -
В Паскале ограничен набор средств для возведения в степень, поэтому во многих случаях можно использовать следующее равенство:
аb=ebln(a),
a>0
Для выполнения данной лабораторной работы необходимо изучить способы записи числовых констант. Ниже приведены примеры записи числовых констант
1,34
,
-0,015
Bарианты заданий
|
ВАРИАНТ ВЫРАЖЕНИЕ |
|
1. z=
|
|
2.y
= sin x + |
|
3.y
=
|
|
4.z
=
|
|
5.z
=
|
|
6.y
= e |
|
7.y
= e |
|
8.y
= e |
|
9.z
=
|
|
10.
z = |
|
11.
y = (sin x) |
|
12.
y = e |
|
13.
y = ln |
|
14.
y = 3 sin x +
|
|
15.
y =
|
|
16.
y = ln
|
|
17.
y = arctg(x + 1) + e |
|
18.
z = 2 cos |
|
19.
z =
|
|
20.
y =
|
|
21.
y = e |
|
22.
y = e |
|
23.
z =
|
|
24.
z =
|
|
25.
z =
|
+sin
,
a = sin x
,z =
e
+
4, 48
10
+ e
- 0, 36
10
+
cos(2x + 5) +
+
+ ln(x
+
5)
+
cos
x
+
+ 1,15
+
+ 10y , y = ln
e
- 0,0012
+
e
-
ln(x
+1)
+
sin
x
+
- 0,14
+
x
- 0,5
+
(x + 5)
+
ln (x
+2)
+
-
ln (x
+4)
+
+
ln (
)
+ 14,48
10
ln
+
+
+
+
- 0,024
10
D.2. Лабораторная работа № 2
Тема:Разветвляющиеся программы.
Цель:Приобретение навыков составления разветвляющихся алгоритмов и программ, приобретение знаний об использовании операторов, обеспечивающих разветвление вычислительных процессов.
Для выполнения этой работы необходимо повторить материал, используемый в лабораторной работе № 1, и изучить следующие вопросы:
Условный и составной операторы, оператор выбора;
Данные логического типа;
Логические выражения, логические операции, операции отношения, их приоритеты. Встроенные функции, дающие результат логического типа.
При отсутствии ограничений на значения исходных данных необходимо проанализировать приведенное в задании выражение с целью выявления области определения указанной функции, т.е. определить те значения исходных данных, при которых получение численного результата невозможно. При этом следует обратить внимание на следующие типовые ситуации, которые могут появляться в процессе вычислений:
Деление на ноль;
Извлечение корня квадратного из отрицательного числа;
Вычисление логарифма отрицательного или нулевого аргумента.
Выполняя работу, следует помнить, что некоторые операции требуют использования общеизвестных математических равенств, например,
аb=
ebln(a) ,
tg x =
, sh x =
и т.д.
Здесь также могут появляться ограничения на возможность получения численного результата работы программы.
После выявления всех вариантов, при которых конечный результат невозможно получить, составляют алгоритм, в котором численный результат выводится в том случае, если это возможно при конкретном сочетании значений исходных данных. Во всех остальных случаях нужно вывести сообщение о невозможности получения численного результата с обязательным указанием причин.
Варианты заданий
|
ВАРИАНТ ВЫРАЖЕНИЕ |
|
1. y =
ln ( |
|
2.y
= ln
|
|
3. |
|
4.y
=
|
|
5. |
|
6.y
= e |
|
7.y
=
|
|
8. |
|
9.y
=
|
|
10.y
= x |
|
11.
y =
|
|
12.y
=
|
|
13.y
=
|
|
14.y
=
|
|
15.y
=
|
|
16.y
=
|
|
17.z
= ln
|
|
18.z
= ln |
|
19.z
=
|
|
20.z
= x |
|
21.z
=
|
|
22.z
=
|
|
23. у
= |
|
24. у
= |
|
25. у
= |
)
- e
+
, a = 0,5
+
,
a = 54
10
-
,
a = 10
+
(sin2x+5x)
,
a = 0,25
;a = 0,4
ln x +
; a = 2,34
10
+
- ln
+arctg
+
;a = 3,5;b = 1,44
/
ln(1+x);a = 16
;a = 0,0034
+
;
a = 0,74
;y = 10
;y = 1,2
+
-
;y = 6,8 ;a
= 0,15
; y = 0,72
