
мат.анализ_23пс / ОКИШЕВ МатАн ТПС / СЕМЕСТР3 группа 22п / Справочник ФРЯ студ / Справочник алгоритмы / Справочник ряд Фурье
.docТРИГОНОМЕТРИЧЕСКИЕ РЯДЫ
Если
![]() является функцией периодической, то
естественно раскладывать ее в
функциональный ряд также по периодическим
функциям, например, по косинусам и
синусам.
является функцией периодической, то
естественно раскладывать ее в
функциональный ряд также по периодическим
функциям, например, по косинусам и
синусам.
О п р е д е л е н и е 8.
Тригонометрическим рядом называется функциональный ряд вида:
 (8)
(8)
или, в более общем виде, ряд:
 ,
(9)
,
(9)
где
![]() – постоянное число, а постоянные числа
– постоянное число, а постоянные числа
![]()
![]() называются коэффициентами
тригонометрического ряда.
называются коэффициентами
тригонометрического ряда.
КОЭФФИЦИЕНТЫ ФУРЬЕ ФУНКЦИИ
На
основе условий ортогональности Фурье
получил формулы коэффициентов
тригонометрического ряда (8), соответствующего
функции
![]() :
:
 ;
(10)
;
(10)
 ,
,
![]() ;
(11)
;
(11)
 ,
,
![]() . (12)
. (12)
ДОСТАТОЧНЫЕ УСЛОВИЯ СХОДИМОСТИ РЯДОВ ФУРЬЕ
( УСЛОВИЯ ДИРИХЛЕ )
Пусть функция
![]() :
:
Д 1. Имеет период
![]() ;
;
Д 2. Кусочно-монотонна на отрезке
![]() ;
;
Д 3. Ограничена на отрезке
![]() .
.
Если функция
![]() удовлетворяет условиям Дирихле, то в
точках непрерывности
удовлетворяет условиям Дирихле, то в
точках непрерывности
![]() на отрезке
на отрезке
![]() имеет место разложение:
имеет место разложение:
 ,
(13)
,
(13)
причем коэффициенты вычисляются по формулам (10) – (12).
РАЗЛОЖЕНИЕ
![]() -ПЕРИОДИЧЕСКИХ
ФУНКЦИЙ В РЯДЫ ФУРЬЕ
-ПЕРИОДИЧЕСКИХ
ФУНКЦИЙ В РЯДЫ ФУРЬЕ
Алгоритм Разложение функции в ряд Фурье.
( краткий вариант )
1)
построить график периодической функции
![]() ;
;
2)
проверить условия Дирихле Д 1 – Д
3, чтобы гарантировать сходимость
ряда Фурье к функции
![]() в точках непрерывности. При невыполнении
этих условий завершить решение задачи;
в точках непрерывности. При невыполнении
этих условий завершить решение задачи;
3)
вычислить коэффициенты Фурье функции
![]() ;
;
4) составить разложение вида (13), указав подмножество числовой прямой, на котором это разложение справедливо.
Ряды для четных и нечетных функций
Если
функция
![]() – четная, а
– четная, а
![]() –нечетная, то
–нечетная, то
 ;
(14)
;
(14)
 .
(15)
.
(15)
Графики
четной и нечетной
![]() -периодических
функций изображены на рис. 3.
-периодических
функций изображены на рис. 3.

а) Четная периодическая функция б) Нечетная периодическая функция
Рис. 3
В случае
четной периодической функции
![]() (рис. 3а) имеем:
(рис. 3а) имеем:
 ;
(16)
;
(16)
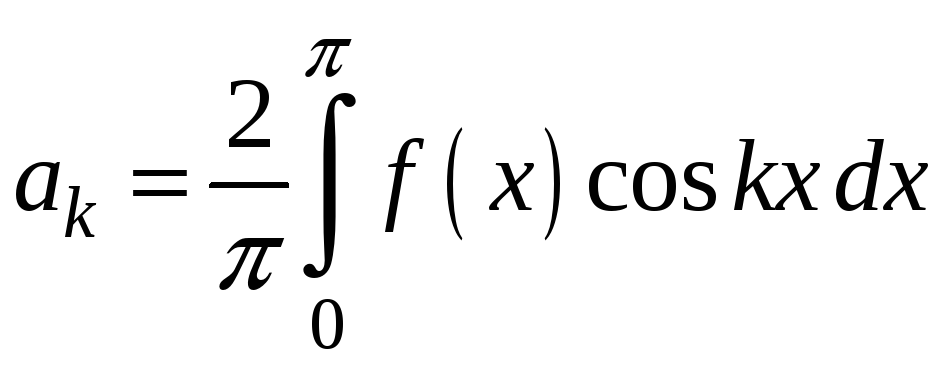 ,
,
![]() ;
(17)
;
(17)
![]() ,
,
![]() .
(18)
.
(18)
Таким
образом, четная функция
![]() раскладывается в ряд Фурье только по
косинусам, а коэффициент
раскладывается в ряд Фурье только по
косинусам, а коэффициент
![]() «регулирует» сдвиг графика функции по
оси ординат.
«регулирует» сдвиг графика функции по
оси ординат.
В случае
нечетной периодической функции
![]() (рис. 3б) имеем:
(рис. 3б) имеем:
![]() ;
(19)
;
(19)
![]() ,
,
![]() ;
(20)
;
(20)
 ,
,
![]() .
(21)
.
(21)
Нечетная
функция
![]() раскладывается в ряд Фурье только по
синусам, а сдвиг графика функции по
оси ординат отсутствует
раскладывается в ряд Фурье только по
синусам, а сдвиг графика функции по
оси ординат отсутствует
![]() .
.
РАЗЛОЖЕНИЕ
![]() -ПЕРИОДИЧЕСКИХ
ФУНКЦИЙ В РЯДЫ ФУРЬЕ
-ПЕРИОДИЧЕСКИХ
ФУНКЦИЙ В РЯДЫ ФУРЬЕ
Так как
число
![]() – произвольное , то в данном разделе
рассматриваются функции с произвольным
периодом Т =
– произвольное , то в данном разделе
рассматриваются функции с произвольным
периодом Т =
![]() .
.
Разложение по основной тригонометрической системе функций
![]() -периодической
функции
-периодической
функции
![]() соответствует ряд Фурье вида:
соответствует ряд Фурье вида:
 ,
(22)
,
(22)
т. е.
![]() раскладывается в ряд по основной
тригонометрической системе
раскладывается в ряд по основной
тригонометрической системе
 .
.
Все изложенное выше для рядов Фурье вида (13) можно перенести на ряды вида (22).
Условия Дирихле и Формулы коэффициентов Фурье
Д 1. Функция
![]() имеет период
имеет период
![]() ;
;
Д 2. Кусочно-монотонна на отрезке
![]() ;
;
Д 3. Ограничена на отрезке
![]() .
.
Общие
формулы коэффициентов Фурье
![]() -периодической
функции
-периодической
функции
![]() :
:
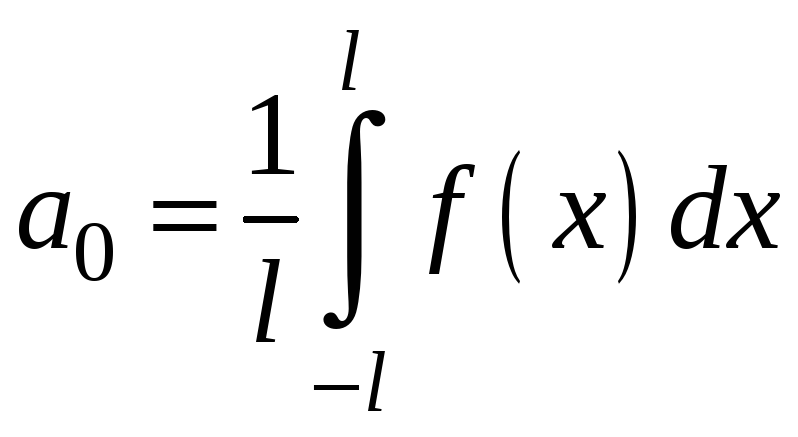 ;
(23)
;
(23)
 ,
,
![]() ;
(24)
;
(24)
 ,
,
![]() . (25)
. (25)
Для
четной
![]() -периодической
функции
-периодической
функции
![]() выполняется:
выполняется:
 ;
(26)
;
(26)
 ,
,
![]() ;
(27)
;
(27)
![]() ,
,
![]() ,
(28)
,
(28)
Для нечетной
![]() -периодической
функции
-периодической
функции
![]() справедливо:
справедливо:
![]() ;
(29)
;
(29)
![]() ,
,
![]() ;
(30)
;
(30)
 ,
,
![]() .
(31)
.
(31)
