мат.анализ_23пс / ОКИШЕВ МатАн ТПС / СЕМЕСТР3 группа 22т / Справочник ФРЯ студ / Справочник приложения / Справочник ряды Фурье

П Р И Л О Ж Е Н И Е ФУРЬЕ-1

СВОЙСТВА ПЕРИОДИЧЕСКИХ ФУНКЦИЙ

Функция , определенная на множестве D, называется периодической с периодом T > 0, если при каждом значение и выполняется равенство .

Очевидно, что, если число Т является периодом функции , то числа вида тТ, где N, также являются ее периодами. Например, . Поэтому обычно рассматривают наименьший период функции.

Простейшими периодическими функциями являются тригонометрические. Функции и имеют наименьший период , и – наименьший период . Для рассматриваемых в данной работе функций из ПТС , наименьший период , а для функций из ОТС , , где N.

Для построения графика периодической функции периода Т достаточно построить его на любом отрезке длины Т и периодически продолжить его во всю область определения.

Основные свойства периодических функций

1) Алгебраическая сумма периодических функций, имеющих один и тот же период Т, есть периодическая функция с периодом Т.

2) Если функция имеет период Т, то функция имеет период : действительно, .

3) Если функция имеет период Т и интегрируема, то при любых R.

П Р И Л О Ж Е Н И Е ФУРЬЕ-2

ВАЖНЕЙШИЕ ОРТОГОНАЛЬНЫЕ СИСТЕМЫ ФУНКЦИЙ

Название ОС	Обозначение и вид функции	Промежуток ортогональности	Весовая функция
Полиномы Чебышева
Полиномы Лежандра			1
Полиномы Лагерра
Полиномы Эрмита
Основная тригонометрическая система			1
Простейшая тригонометрическая система			1
Простейшая система косинусов			1
Простейшая система синусов			1

П Р И Л О Ж Е Н И Е ФУРЬЕ-3

ПОЛЕЗНЫЕ ФОРМУЛЫ ДЛЯ ВЫЧИСЛЕНИЯ КОЭФФИЦИЕНТОВ ФУРЬЕ

1) Интегралы произведений степенной и тригонометрической функций:

(п. 3.1)

(п. 3.2)

(п. 3.3)

(п. 3.4)

2) Интегралы произведений синусов и косинусов:

(п. 3.5)

(п. 3.6)

(п. 3.7)

3) Значения синусов и косинусов:

(п. 3.8)

(п. 3.9)

(п. 3.10)

(п. 3.11)

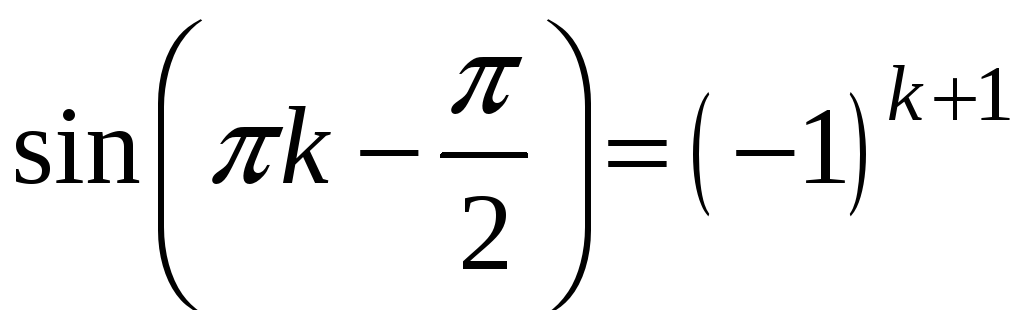
(п. 3.12)

(п. 3.13)

(п. 3.14)

П Р И Л О Ж Е Н И Е ФУРЬЕ-4

РАЗЛОЖЕНИЕ ПО ГАРМОНИКАМ

Пусть функции поставлен в соответствие ее ряд Фурье:

.

Для любого натурального k имеет место тождество:

, где , а , – величина, однозначно определяемая из уравнений:

, .

Следовательно, ряд Фурье можно записать также в виде функционального ряда:

,

члены которого называют гармоническими колебаниями (или гармониками). При этом A_k называют амплитудой колебания, к – циклической (круговой) частотой, а – начальной фазой колебания. Равенство

,

если оно имеет место, называют разложением функции в сумму гармонических колебаний (гармоник). При использовании функций времени в прикладных задачах циклическую частоту обозначают , причем называют основной частотой. Тогда

.

П Р И Л О Ж Е Н И Е ФУРЬЕ-5

АППРОКСИМАЦИЯ ТРИГОНОМЕТРИЧЕСКИМИ ПОЛИНОМАМИ

Выражение вида , обычно называют тригонометрическим полиномом (тригонометрическим многочленом), а параметр п – порядком тригонометрического многочлена. Как видим, есть не что иное, как «кусок тригонометрического ряда» до п – го члена включительно.

Т е о р е м а В е й е р ш т р а с с а.

Если функция непрерывна на отрезке и удовлетворяет условию , то эту функцию можно равномерно на отрезке приблизить тригонометрическими полиномами, т. е. существует бесконечная последовательность, такая что I на .

Итак, среди тригонометрических полиномов есть «хорошо аппроксимирующие» непрерывную периодическую функцию . Выбор наилучшей аппроксимации для функции на отрезке зависит от способа измерения расстояния между и .

Если за меру погрешности взять так называемое среднее квадратическое отклонение , которое определяется равенством:

то окажется, что наименьшую величину среди всех тригонометрических многочленов порядка п дает многочлен, коэффициенты которого являются коэффициентами Фурье функции . Итак, частичные суммы ряда Фурье являются наилучшими аппроксимациями порождающей функции . Доказательство этого факта изложено, например, в учебнике [1].

П Р И Л О Ж Е Н И Е ФУРЬЕ-6

СХОДИМОСТЬ КОЭФФИЦИЕНТОВ ФУРЬЕ К НУЛЮ

При аппроксимации функций тригонометрическими полиномами требуется, чтобы остаток ряда Фурье стремился к нулю при , что достигается, если коэффициенты и стремятся к нулю. Важна также скорость сходимости коэффициентов Фурье к нулю, чтобы оценить, сколько членов ряда следует сохранить в аппроксимирующем полиноме .

Если ряд Фурье функции сходится, то и исходя из необходимого признака сходимости функционального ряда (). Стремление коэффициентов Фурье к нулю может следовать из свойств порождающей функции .

У т в е р ж д е н и е. Если функция – кусочно непрерывна и ограничена на отрезке , то ее коэффициенты Фурье стремятся к нулю при , т. е. .

Скорость сходимости коэффициентов Фурье к нулю (порядок их малости) зависит от степени гладкости (дифференцируемости) раскладываемой в тригонометрический ряд функции.

Т е о р е м а. Пусть функция имеет на отрезке непрерывные производные до порядка т включительно и кусочно непрерывную производную порядка т + 1, причем выполняются условия:

, , …, .

Тогда ее коэффициенты Фурье удовлетворяют соотношениям:

, , .

Подробное доказательство приведенных теорем изложено в работах [1], [2]. Таким образом, по свойствам исходной функции можно подобрать требуемый порядок аппроксимирующего тригонометрического многочлена .

П Р И Л О Ж Е Н И Е ФУРЬЕ-7

КОМПЛЕКСНАЯ ФОРМА РЯДА ФУРЬЕ

Любой тригонометрический ряд может быть записан в комплексной форме. Для этого используются формулы Эйлера, выражающие косинус и синус через показательную функцию:

(п. 7.1)

Согласно курсу лекций [3], ряд Фурье функции преобразуется тогда к новому виду:

, (п. 7.2)

где , , . (п. 7.3)

Обычно формула (п. 7.2) записывается в более кратком виде:

. (п. 7.4)

Коэффициенты этого ряда вычисляются по формуле:

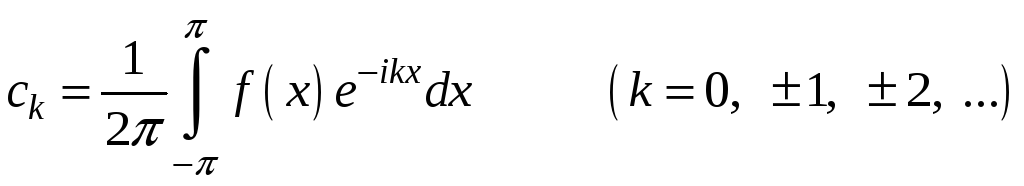. (п. 7.5)

Равенство (п. 7.4) называется комплексной формой ряда Фурье функции , а числа , найденные по формуле (п. 7.5) – комплексными коэффициентами ряда Фурье.

Если функция задается на отрезке , то комплексная форма ее ряда Фурье имеет вид:

, (п. 7.6)

а коэффициенты Фурье вычисляются по формуле:

. (п. 7.7)

В электротехнике и радиотехнике члены ряда называются гармониками, коэффициенты с_k – комплексными амплитудами гармоник, а числа – волновыми числами функции .

Совокупность величин называется амплитудным спектром. Спектр периодической функции , будучи гармоническим (частоты кратны одному и тому же числу ), является дискретным или линейчатым. Графически амплитудный спектр можно изобразить в виде вертикальных отрезков с длинами , расположенных в точках числовой оси.

Обратите внимание, что линейчатый спектр симметричен относительно начала координат, так как числа и являются комплексно сопряженными и их модули равны: .

П Р И Л О Ж Е Н И Е ФУРЬЕ-8

ПРОДОЛЖЕНИЕ ФУНКЦИИ, ЗАДАННОЙ НА ПРОИЗВОЛЬНОМ ОТРЕЗКЕ

В разделе 6 рассмотрены три основных периодических продолжения функции , заданной на отрезке . В случае задания на произвольном отрезке разложение в ряд Фурье несколько усложняется (см. рисунок).

Сначала перенесем начало системы координат в середину отрезка , а именно в точку , заменой переменных . Далее продолжим функцию периодическим образом на всю числовую прямую, т. е. рассмотрим новую функцию . Полупериодом этой функции будет половина длины отрезка , т. е. величина . Сопоставим функции ряд Фурье, имеем:

.

Последняя формула цепочки преобразований является разложением исходной функции в ряд Фурье на отрезке . При этом ортогональная система косинусов и синусов отлична от ПТС и ОТС.

17