
мат.анализ_23пс / ОКИШЕВ МатАн ТПС / СЕМЕСТР3 группа 22т / Справочник ФРЯ студ / Справочник алгоритмы / Справочник ряд Тейлора
.doc
РАЗЛОЖЕНИЕ В РЯД ТЕЙЛОРА И РЯД МАКЛОРЕНА
ОСНОВНЫЕ ПОНЯТИЯ
О
п р е д е л е н и е 7. Пусть функция f(x)
задана в некоторой окрестности точки
![]() и имеет в этой точке производные любого
порядка. Тогда степенной ряд
и имеет в этой точке производные любого
порядка. Тогда степенной ряд
 R,
(4)
R,
(4)
называют
рядом Тейлора
функции f(x)
в точке
![]() .
При
.
При
![]() = 0 ряд Тейлора называют рядом
Маклорена.
Он имеет вид:
= 0 ряд Тейлора называют рядом
Маклорена.
Он имеет вид:
 .
(5)
.
(5)
Ряд
Тейлора (4) есть степенной ряд общего
вида с коэффициентами
 и интервалом сходимости
и интервалом сходимости
![]() ,
где R
– радиус сходимости.
,
где R
– радиус сходимости.
Ряд
Маклорена (5) – это степенной ряд с
коэффициентами
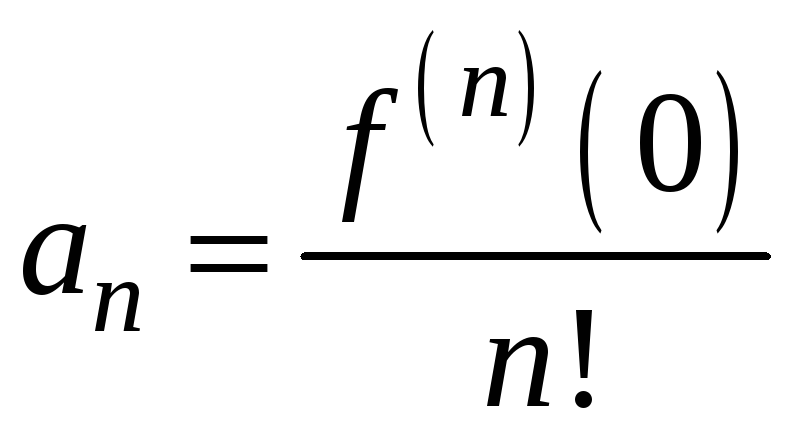 ,
а его интервал сходимости –
,
а его интервал сходимости –
![]() .
.
.
.
Равенства-разложения
 (6)
(6)
и
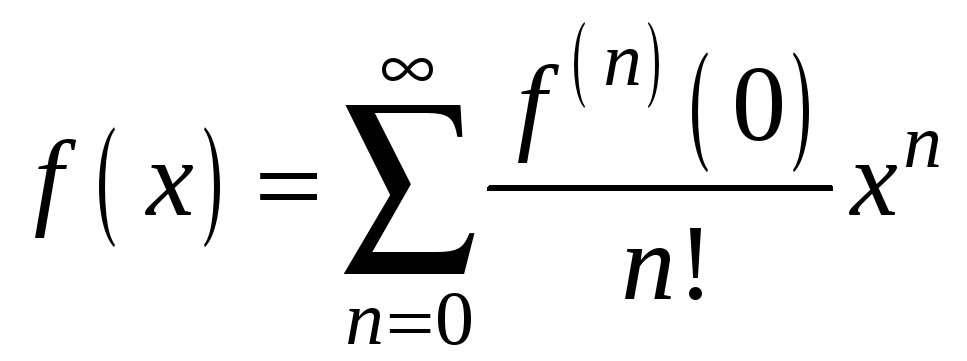 (7)
(7)
справедливы
лишь в том случае, если остаточный член
![]()
![]() при
при
![]() .
.
АЛГОРИТМ РАЗЛОЖЕНИЯ В РЯД ТЕЙЛОРА С ПОМОЩЬЮ
ДИФФЕРЕНЦИРОВАНИЯ ИСХОДНОЙ ФУНКЦИИ
Так
как основной частью коэффициента ряда
Тейлора
 является значение производной п-го
порядка функции f(x)
в точке
является значение производной п-го
порядка функции f(x)
в точке
![]() ,
то можно составить ряд Тейлора функции
f(x),
последовательно находя значения ее
производных при
,
то можно составить ряд Тейлора функции
f(x),
последовательно находя значения ее
производных при
![]() .
.
Алгоритм А1 Разложение в ряд Тейлора дифференцированием.
Функцию
f(x)
требуется разложить в ряд вида
 и определить интервал
и определить интервал
![]() ,
в котором это разложение верно, т. е.
выполняется равенство (6). Нужно выполнить
следующие действия:
,
в котором это разложение верно, т. е.
выполняется равенство (6). Нужно выполнить
следующие действия:
-
найти производные

-
вычислить значения производных в точке
 ;
; -
найти общую формулу
 и составить ряд (4);
и составить ряд (4); -
найти интервал сходимости ряда
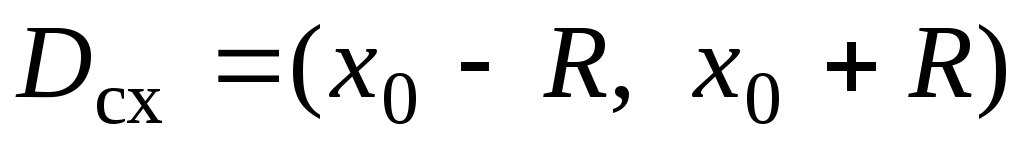 ;
; -
определить точки
 ,
где
,
где

 =
0, т. е. точки, в которых раз-
=
0, т. е. точки, в которых раз-
ложение функции f(x) справедливо.
З
а м е ч а н и е. В алгоритме А1
четвертый шаг мы будем выполнять
частично, не проверяя сходимость ф. р.
(4) в граничных точках
![]() ,
а пятый шаг будем считать выполнившимся
автоматически:
все f(x)
будут у нас элементарными, и поэтому
,
а пятый шаг будем считать выполнившимся
автоматически:
все f(x)
будут у нас элементарными, и поэтому
![]()
![]() при
при
![]() для всех
для всех
![]() .
.
На
практике часто ограничиваются получением
нескольких начальных членов ряда, что
соответствует аппроксимации функции
f(x)
многочленом Тейлора
![]() в некоторой окрестности точки
в некоторой окрестности точки
![]() .
Построение именно таких аппроксимаций
требуется выполнить в задачах типового
расчета на алгоритм А1.
.
Построение именно таких аппроксимаций
требуется выполнить в задачах типового
расчета на алгоритм А1.
СТАНДАРТНЫЕ РАЗЛОЖЕНИЯ В СТЕПЕННЫЕ РЯДЫ
При помощи алгоритма А1 для многих простейших функций f(x) были получены разложения в ряды Тейлора. Особенно часто используется таблица рядов Маклорена для некоторых основных элементарных функций, в которую в разных учебниках включается разное количество формул.
ТАБЛИЦА РЯДОВ МАКЛОРЕНА
1)
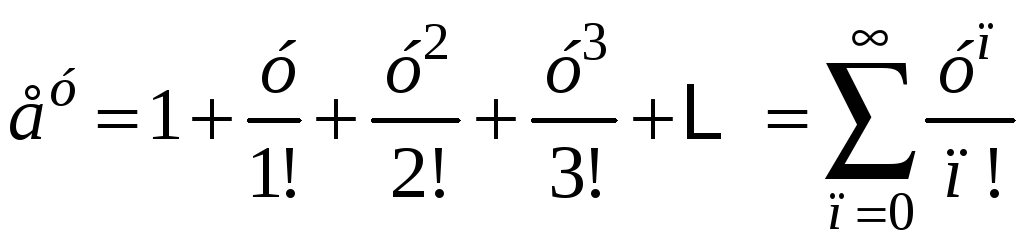 ,
,
![]() R.
R.
2)
 ,
,
![]() R.
R.
3)
 ,
,
![]() R.
R.
4)
 ,
,
![]() .
.
5)
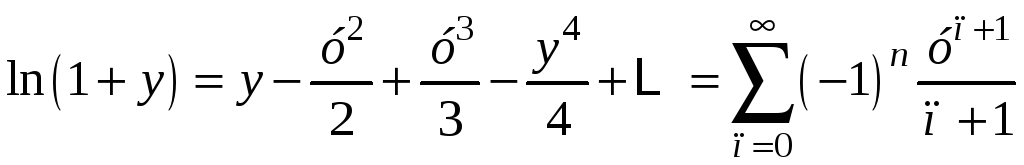 ,
,
![]() .
.
6)
 ,
,
![]() R.
R.
7)
 ,
,
![]() R.
R.
8)
 ,
,
![]() .
.
АЛГОРИТМ РАЗЛОЖЕНИЯ В РЯД ТЕЙЛОРА
КОМБИНИРОВАНИЕМ ИЗВЕСТНЫХ РЯДОВ
Алгоритм А2 Разложение в ряд Тейлора комбинированием.
Функцию f(x) требуется разложить в ряд Тейлора или Маклорена. Область, где найденное разложение будет верным, определяется на основе свойств операций над степенными рядами. Для решения задачи выполняются следующие действия:
-
представить функцию f(x) как комбинацию функций, разложения ко-
торых известны;
-
подставить в выражение f(x) ряды для отдельных компонент;
-
выполнить операции над рядами;
-
определить интервал сходимости комбинации рядов.
З а м е ч а н и е. Часто в задачах используются неполный (упрощенный) вариант алгоритма А2 и нестандартные, вновь полученные исследователем (студентом) разложения функций в ряды Тейлора.
Хотя
алгоритм реализуется на основе
таблицы
рядов Маклорена,
применение замен переменных позволяет
получать с его помощью ряды Тейлора
для
![]() .
Кроме того, идея алгоритма может быть
применена для комбинирования рядов
Тейлора по степеням
.
Кроме того, идея алгоритма может быть
применена для комбинирования рядов
Тейлора по степеням
![]() при одинаковом центре
разложения
при одинаковом центре
разложения
![]() .
.
