мат.анализ_23пс / ОКИШЕВ МатАн ТПС / СЕМЕСТР3 группа 22т / Справочник ФРЯ студ / Справочник задачи / Справочник задачи СХ

1. ПРИМЕРЫ НАХОЖДЕНИЯ ОБЛАСТЕЙ СХОДИМОСТИ

ФУНКЦИОНАЛЬНЫХ РЯДОВ

З а д а ч а 1. Найти область сходимости функционального ряда

.

Решение. Прежде всего найдем область определения ф. р. Знаменатели дробей не равны нулю, откуда . Поэтому R Определим вспомогательную функцию . Выпишем формулы -го и -го членов ф. р.: ; .

Тогда

Таким образом,

Решим неравенство . Обычно неравенства на простейшие функции удобно решать графически, но при этом требуется знать графики основных элементарных функций. Исходный вид неравенства задачи – это соотношение (1), но от него можно перейти к эквивалентным соотношениям (2) или (3):

(1)

(2)

(3)

Графическое решение неравенств (1), (2) и (3) показано соответственно на рис. 1, 2 и 3. В первом случае строится график нелинейной функции с бесконечным разрывом 2-го рода, во втором – сдвинутый в точку график модуля, в третьем – линейная зависимость. Получающаяся область сходимости выделена на оси жирной линией. Как видим, несмотря на различие графиков изображаемых на рисунках функций получается одной и той же и является объединением двух бесконечных интервалов.

Рис. 1 Рис. 2

Рис. 3

Выбор варианта графического решения неравенства остается за исследователем (студентом). Простейший вид функций привел к тому, что точка не попадает в найденные интервалы и , и требование выполнилось автоматически. При и ф. р. расходится. В граничных точках и сходимость неизвестна, но мы исключим их из . Тогда .

Более подробное исследование сходимости в точках и приводит к числовым рядам и . Сходимость первого устанавливается по признаку Лейбница, а второй ряд расходится по интегральному признаку Коши (см. приложение).

Ответ. Областью сходимости ф. р. можно считать . Полное исследование добавляет в одну точку , т. е. окончательно .

З а д а ч а 2. Найти область сходимости функционального ряда

.

Решение. Функции определены на всей числовой прямой, так как взятие синуса и извлечение кубического корня возможны для всех R. Таким образом, R, что никак не ограничивает . Найдем вспомогательную функцию . Имеем:

; . Тогда

Таким образом,

Решим неравенство Очевидно, что для всех R , так как . Остается лишь исключить точки, где , т. е. где . На рис. 4 видно, что это точки Z .

В точках и сходимость ф. р. неизвестна. Исключая точки , имеем: R Z . Этот же результат можно записать как счетное объединение интервалов: Форму записи результата исследователь (студент) выбирает самостоятельно.

Рис. 4

Более подробное исследование в точках, где , приводит к числовому ряду , а в точках, где , к числовому ряду . Для обоих рядов не выполняется необходимый признак сходимости, и ряды расходятся.

Ответ. Область сходимости ряда есть множество R Z . Полное исследование с помощью числовых рядов не вносит в результат никаких изменений.

З а д а ч а 3. Найти область сходимости функционального ряда

.

Решение. В данной задаче операция извлечения квадратного корня справедлива лишь при . Поэтому имеем область определения ряда . Найдем функцию . Имеем:

; . Тогда

.

Таким образом,

Решим неравенство . Получаем цепочку эквивалентных неравенств: Эта цепочка представляет собой аналитическое решение требуемого неравенства на функцию , но результат будет неверен, если не учесть область . Графическое решение второго из неравенств цепочки показано на рис. 5. Область определения ф. р. уже учтена на рисунке, а область сходимости представляет собой один промежуток числовой прямой: .

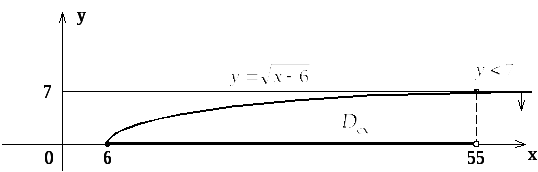
Рис. 5

Дополнительное исследование граничной точки , где , приводит к числовому ряду , сумма которого равна бесконечности.

Ответ. Область сходимости функционального ряда есть множество . Исследование с помощью числовых рядов не меняет этот результат.

____________________________________________________________________

Рассмотрев примеры работы алгоритма поиска области сходимости функционального ряда, мы обнаружили различные виды областей сходимости: объединение двух бесконечных интервалов; счетное объединение конечных интервалов равной длины; один конечный интервал. Далее переходим к получению областей сходимости степенных рядов.

2. ПРИМЕРЫ НАХОЖДЕНИЯ ОБЛАСТЕЙ СХОДИМОСТИ

СТЕПЕННЫХ РЯДОВ

При нахождении для степенного ряда нет необходимости решать неравенства и делать какие-либо графические иллюстрации. Поэтому будем лишь находить радиус сходимости и область сходимости в виде открытого интервала . Исследование концов интервала сходимости, т. е. граничных точек , оставляется читателю в качестве самостоятельного упражнения.

З а д а ч а 4. Найти радиус и интервал сходимости для следующих степенных рядов:

Решение. При нахождении радиуса и области сходимости степенного ряда вначале проверяется его полнота, а из общего члена ряда выделяются коэффициент и центр области сходимости – точка .

____________________________________________________________________

Ряд является полным, . Применим формулу Даламбера (RD) и, учитывая, что , имеем:

Таким образом, радиус сходимости , а область сходимости есть вся числовая прямая: R .

____________________________________________________________________

Ряд перепишем в виде . Рассматриваемый ряд является полным, . Для нахождения радиуса сходимости удобно применить формулу Коши (RK), удаляющую возведение в -ю степень:

.

Таким образом, радиус сходимости , а область сходимости состоит из одной точки , в которой ряд вырождается в бесконечную сумму нулей. Конечно, эта сумма равна нулю, но сам ряд вряд ли полезен для практического применения.

____________________________________________________________________

Ряд полный, причем . По формуле Даламбера (RD), учитывая, что , имеем:

Итак, , а область сходимости .

____________________________________________________________________

Ряд неполный, причем . Что касается остальных данных, то . Применим «измененную» формулу Даламбера (RDN) и, учитывая, что , имеем:

Получили куб радиуса сходимости: . Отсюда , а область сходимости четвертого ряда .

____________________________________________________________________

При решении задачи 4 обнаружились четыре основных ситуации сходимости степенных рядов: область сходимости, совпадающая с R; вырождение области сходимости в точку; интервал сходимости вида , несимметричный относительно ; интервал сходимости вида , симметричный относительно нуля.

9