Энтропия источника дискретных сообщений

А. Энтропия источника независимых сообщений

Мы определили количество информации, содержащееся в отдельном сообщении. Во многих случаях, например при согласовании канала с источником информации, возникает необходимость в характеристиках, позволяющих оценивать информационные свойства источника сообщений в целом. Одной из важнейших характеристик такого типа является среднее количество информации, приходящееся на одно сообщение.

В простейшем случае, когда все сообщения равновероятны, количество информации в каждом из них одинаково и равно

При этом среднее количество информации равно . Следовательно, при равновероятных независимых сообщениях информационные свойства источника зависяттолько от числа сообщений в ансамбле m.

Однако в реальных условиях сообщения, как правило, имеют разную вероятность. Например, буквы О, Е и А встречаются в тексте сравнительно часто, тогда как Щ, Ы и Ъ – достаточно редко. Поэтому знания числа сообщений m в ансамбле недостаточно и требуется иметь сведения о вероятности каждого сообщения . Так как вероятности сообщений неодинаковы, то они несут различное количество информации:

Среднее количество информации, приходящееся на одно сообщение источника, определяется как математическое ожидание :

Величина называетсяэнтропией. Этот термин заимствован из термодинамики, где он характеризует неопределенность состояния физической системы.

В теории информации энтропия также характеризует неопределенность ситуации до передачи сообщения, поскольку заранее неизвестно, какое из сообщений будет передано. Важно понимать, что чем больше энтропия, тем сильнее неопределенность и тем большую информацию в среднем несет одно сообщение источника.

В качестве примера вычислим энтропию источника сообщений, когда ансамбль сообщений состоит лишь из двух сообщений и, характеризуемых вероятностями. Энтропия такого источника в соответствии с (10) будет равна

Зависимость энтропии от величины p приведена на Рис. 1.

Рис. 1. Зависимость энтропии от вероятности

Максимум энтропии имеет место при , т.е. когда ситуация является наиболее неопределенной. Приили, что соответствует передаче одного из сообщенийили, неопределенностьотсутствует. В этих случаях энтропия равна нулю.

Среднее количество информации, содержащееся в последовательности из n сообщений, равно

Отсюда следует, что количество передаваемой информации можно увеличить не только за счет числа сообщений, но и путем повышения энтропии источника, т.е. информационной емкости его сообщений.

Обобщая эти результаты, можно сформулировать основные свойства энтропии источника независимых сообщений:

• Энтропия – величина всегда положительная, так как ;

• При равновероятных сообщениях, когда

энтропия максимальна и равна

• Энтропия равняется нулю лишь в тех случаях, когда все вероятности равны нулю, за исключением одной, величина которой равна единице;

• Энтропия нескольких независимых источников равна сумме энтропий этих источников

Б. Энтропия источника зависимых сообщений

Рассмотренный нами источник независимых сообщений является простейшим типом источника. В реальных условиях картина значительно усложняется из-за наличия статистических связей между сообщениями. Примером может служить обычный текст, где появление той или иной буквы зависит от предыдущих буквенных сочетаний. Так например, после сочетания ЧТ вероятность следования гласных букв О, Е или И значительно выше, чем согласных.

Статистическая связь ожидаемого сообщения с предыдущим сообщением количественно оценивается совместной вероятностью или условной вероятностью, которая выражает вероятность появления сообщенияпри условии, что известно предыдущее сообщение . Количество информации, содержащейся в сообщении при условии, что известно предыдущее сообщение согласно (1) будет равно

Среднее количество информации при этом определяется условной энтропией , которая вычисляется как математическое ожидание информации по всем возможным сообщениям.

Важным свойством условной энтропии источника зависимых сообщений является то, что при неизменном количестве сообщений в ансамбле источника его энтропия уменьшается с увеличением числа сообщений, между которыми существует статистическая взаимосвязь. В соответствии с этим свойством, а также свойством энтропии источника независимых сообщений можно записать неравенства

Таким образом, наличие статистических связей между сообщениями всегда приводит к уменьшению количества информации, приходящейся в среднем на одно сообщение.

Избыточность источника сообщений

Уменьшение энтропии источника с увеличением статистической взаимосвязи (14) можно рассматривать как снижение информационной емкости сообщений. Одно и то же сообщение при наличии взаимосвязи содержит в среднем меньше информации, чем при ее отсутствии. Иначе говоря, если источник создает последовательность сообщений, обладающих статистической связью, и характер этой связи известен, то часть сообщений, выдаваемых источником, является избыточной, так как она может быть восстановлена по известным статистическим связям. Появляется возможность передавать сообщения в сокращенном виде без потери информации. Например при передаче телеграммы из текста исключаются союзы, предлоги, знаки препинания, так как они легко восстанавливаются при чтении телеграммы на основании известных правил построения фраз и слов.

Говорят, что любой источник зависимых сообщений обладает избыточностью. Количественное определение избыточности может быть получено из следующих соображений. Для того чтобы передать количество информации , источник без избыточности должен выдать в среднемсообщений, а источник с избыточностьюсообщений.

Поскольку и, то для передачи одного и того же количества информации источник с избыточностью должен использоватьбольшее количество сообщений. Избыточное количество сообщений равно , а избыточность определяется как отношение

Величина избыточности согласно (14) является неубывающей функцией. Для русского языка, например, избыточность составляет порядка 50%.

Коэффициент

называется коэффициентом сжатия. Он показывает, до какой величины можно сжать передаваемые сообщения, если устранить избыточность. В связи с тем, что обладающий избыточностью источник передает излишнее количество сообщений, увеличивается продолжительность передачи и снижается эффективность использования канала связи. Требуется проводить сжатие сообщений, которое реализуется с помощью соответствующего кодирования. Информацию необходимо передавать такими сообщениями, емкость которых используется наиболее полно.

Вместе с тем избыточность источника далеко не всегда является отрицательным свойством. Наличие взаимосвязи между буквами текста дает возможность восстановить его при искажении отдельных букв, т.е. использовать избыточность для повышения достоверности передачи информации.

Лекция 6. Пропускная способность дискретных каналов и эффективность систем передачи информации

Скорость передачи информации и пропускная способность дискретного канала без помех

Так как передача информации происходит во времени, естественно ввести понятие скорости передачи как количество информации, передаваемой в среднем за единицу времени

Здесь - количество информации, содержащейся в последовательности сообщений, общая длительность которых равнаT.

Количество информации, создаваемое источником сообщений в среднем за единицу времени, называется производительностью источника . Эту величину удобно выразить через энтропию источника. Приможно считатьи, гдеn – число сообщений, а - средняя продолжительность одного сообщения. Подставляя в (1) значенияи, получим

Величина для независимых сообщений может быть вычислена как математическое ожидание

где - вероятность сообщениядлительностью. Если длительность всех сообщений одинакова и равна, формула (2) принимает вид

Отсюда следует, что наибольшей производительностью обладает источник с максимальной энтропией (см. ф.(12) прошлой лекции), т.е.

Выданная источником информация в виде отдельных сообщений поступает в канал связи, где осуществляется кодирование и ряд других преобразований, в результате которых информация переносится уже сигналами , имеющими другую природу и в общем случае обладающими другими статистическими характеристиками. Для сигналов также может быть найдена скорость передачи по каналу связи

Высокая скорость передачи является одним из основных требований, предъявляемых к системам передачи информации. В реальных условиях всегда существует ряд причин, ведущих к ее ограничению.

Во-первых, в реальном канале число используемых сигналов всегда конечно и энтропия в соответствии с ф.(12) прошлой лекции, есть величина ограниченная

С другой стороны, уменьшение длительности сигнала приводит к расширению спектра, что при учете ограниченной полосы пропускания канала ставит предел уменьшению средней длительности .

Максимально возможная скорость передачи информации по каналу связи называется пропускной способностью канала

Максимум скорости R здесь ищется по всем возможным ансамблям сигналов u .

Пусть число используемых сигналов не превышает m, а их длительность не может быть меньше  секунд. Так как инезависимы, то по формуле (8) следует искать максимуми минимум, что дает

Для двоичных сигналов m = 2 и пропускная способность

Оптимальное статистическое кодирование сообщений

Для дискретных каналов без помех Шенноном была доказана следующая теорема: если производительность источника меньше пропускной способности канала (), то всегда существует способ кодирования, позволяющий передавать по каналу все сообщения источника. Передачу всех сообщений приосуществить невозможно.

Смысл теоремы сводится к тому, что, как бы ни была велика избыточность источника, все его сообщения могут быть переданы по каналу, если .

Для рационального использования пропускной способности канала необходимо применять соответствующие способы кодирования сообщений.

Статистическим или оптимальным называется кодирование, при котором наилучшим образом используется пропускная способность канала без помех. При оптимальном кодировании фактическая скорость передачи информации по каналу R приближается к пропускной способности C, что достигается путем согласования источника с каналом. Сообщения источника кодируются таким образом, чтобы они в наибольшей степени соответствовали ограничениям, которые накладываются на сигналы, передаваемые по каналу связи. Поэтому структура оптимального кода зависит как от статистических характеристик источника, так и от особенностей канала.

Рассмотрим основные принципы оптимального кодирования на примере источника независимых сообщений, который необходимо согласовать с двоичным каналом без помех. Здесь процесс кодирования заключается в преобразовании сообщений источника в двоичные кодовые комбинации. Поскольку существует однозначное соответствие между сообщениями источника и комбинациями кода, то энтропия кодовых комбинаций равна энтропии источника

а скорость передачи в канале определяется с помощью (6) как

Здесь - средняя длительность кодовой комбинации, которая в общем случае неравномерного кода записывается по аналогии с (3) как

где - длительность одного элемента кода и- число элементов в комбинации, присваиваемой сообщению.

Подстановка в формулу (12) выражений

и (13) дает

в котором числитель определяется исключительно статистическими свойствами источника, а величина - характеристиками канала.

Возникает вопрос: можно ли так закодировать сообщение, чтобы скорость передачи (14) достигала своего максимального значения, равного пропускной способности двоичного канала . Легко заметить, что это условие выполняется, если

что соответствует минимуму и максимумуR.

Одним из кодов, удовлетворяющих условию (33), является код Шеннона – Фано, который мы рассмотрим позднее.

Необходимо подчеркнуть, что при оптимальном способе кодирования в сигналах, передающих сообщения источника, совершенно отсутствует избыточность. Устранение избыточности приводит к тому, что процесс декодирования становится весьма чувствительным к воздействию помех. Это особенно сильно проявляется при оптимальном кодировании зависимых сообщений. Иногда одна единственная ошибка может вызвать неправильное декодирование всех последующих сигналов. Поэтому оптимальные коды применимы только для каналов с чрезвычайно низким уровнем помех.

Скорость передачи информации и пропускная способность дискретных каналов с помехами

Каналы без помех характеризуются тем, что количество принятой на выходе канала информации всегда равно количеству информации, переданной источником сообщений.

При этом, если на вход канала поступил сигнал , то на выходе возникает сигнал,однозначно определяющий переданный сигнал . Количество информации, прошедшее по каналу без помех в случае передачии приема, равно количеству информации, содержащейся в сигнале:

Здесь величина вероятности характеризует ту неопределенность в отношении сигнала, которая существоваладо его передачи. После приема в силу однозначного соответствия междуинеопределенность полностью устраняется.

Совершенно другое положение имеет место для каналов, где присутствуют различного рода помехи.

Воздействие помех на передаваемый сигнал приводит к необратимой потере части информации, поступающей от источника сообщений. Так как в канале с помехами принятому сигналу может соответствовать передача одного из нескольких сигналов , то после приемаостается некоторая неопределенность в отношении переданного сигнала. Здесь соответствие междуиноситслучайный характер, и степень неопределенности характеризуется условной апостериорной вероятностью . Количество информации, необходимое для устранения оставшейся неопределенности

очевидно, равно той части информации, которая была потеряна вследствие помех. Количество принятой информации определяется как (см. ф. (9) прошлой лекции)

Для оценки среднего количества принятой информации при передаче одного сообщения выражение (17) необходимо усреднить по всему ансамблю и:

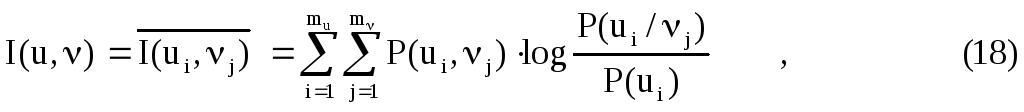
где - совместная вероятность переданного и принятого сигналов,- количество сигналов в ансамбле на входе канала и- количество сигналов в ансамбле на выходе канала (в общем случае).

Величина характеризует в среднем количество информации, которое содержит принятый сигналотносительно переданного сигналаи называетсясредней взаимной информацией между и.

Выражение (18) можно представить в виде

где

представляет энтропию источника сигналов и

- условная энтропия или ненадежность.

Формула (19) показывает, что среднее количество принятой информации равно среднему количеству переданной информации минус среднее количество информации, потерянное в канале вследствие воздействия помех.

Понятия скорости передачи информации и пропускной способности используются и для каналов с помехами. В этом случае скорость передачи информации по каналу можно представить в виде

Пропускная способность канала с помехами определяется как максимально возможная скорость передачи при ограничениях, накладываемых на передаваемые сигналы

Для каналов с сигналами одинаковой длительности , пропускная способность равна

где максимум ищется по всем возможным ансамблям сигнала .

Выведем выражение для пропускной способности двоичного канала с помехами, по которому передаются независимые дискретные сигналы с априорными вероятностями. На выходе канала образуются сигналы, при правильном приеме отражающие сигналы. В результате действия помех возможны ошибки, которые характеризуются при передачеусловной вероятностью, а при передаче- условной вероятностью.

Будем полагать, что канал симметричен, т.е. для него вероятности переходов одинаковы , а полная вероятность ошибки равна

При этих условиях можно показать, что пропускная способность двоичного симметричного канала равна

На Рис. 1. приведена зависимость пропускной способности канала С от вероятности ошибки для двоичного канала согласно формуле (26)

Рис. 1. Зависимость пропускной способности двоичного канала от вероятности ошибки .

Видно, что увеличение вероятности ошибки приводит к снижению пропускной способности, которая становится равной нулю при= 0,5. В этом случае полностью исчезает какая-либо зависимость между передаваемым и принятым сигналами. Таким образом, значение = 0,5 для бинарного симметричного канала является предельным.

Теорема Шеннона для дискретного канала с помехами

Данная теорема имеет фундаментальное значение для теории и техники передачи информации.

Если производительность источника не превышает пропускной способности дискретного канала с помехами (), то существует способ кодирования, позволяющий передать все сообщения источника со сколь угодно малой вероятностью ошибки. Притакая передача невозможна.

Таким образом, наличие помех в канале не препятствует передаче сообщений со сколь угодно малой вероятностью ошибок декодирования, а лишь ограничивает максимальную скорость передачи информации С. Высокая достоверность декодирования и конечная скорость передачи не исключают друг друга.

Вместе с тем теорема не указывает конкретного способа наилучшего кодирования. До сих пор продолжаются поиски способов кодирования, которые позволяли бы с аппаратурой приемлемой сложности достигать предельных возможностей, указанных теоремой Шеннона.

Пропускная способность непрерывного канала. Формула Шеннона

Шенноном была получена также формула для пропускной способности непрерывного канала, в котором помехой является аддитивный шум . Если средние мощности сигнала и шума ограничены величинами, и ширина их спектра равнаF, то формула Шеннона имеет вид

Данная формула очень важна, т.к. она показывает те предельные возможности, к которым следует стремиться при разработке систем передачи информации. Формула выведена для равномерных спектров сигнала и шума, но может быть распространена и на более реальный случай неравномерных спектров. Оказывается, при заданных спектрах сигнала и шума максимума пропускной способности можно добиться путем увеличения мощности сигнала на тех частотах, где уменьшается мощность шума и наоборот. Минимальная пропускная способность соответствует равномерному спектру шума, т.е. “белый шум” является самым вредным видом помех.

Эффективность систем передачи информации

Пропускная способность канала связи С является тем пределом, которого можно достигнуть при идеальном кодировании. Естественно, что в реальных каналах скорость передачи всегда будет меньше С. Степень отличия R от С зависит от того, насколько рационально выбрана и эффективно используется та или иная система передачи информации. Наиболее общей оценкой эффективности системы передачи информации является коэффициент использования канала

Для дискретных систем передачи информации справедливо соотношение , гдеи- эффективностьсистемы кодирования и эффективность системы модуляции соответственно.

Вводя избыточность сообщения и избыточностьсигнала , можно показать, что

где -полная избыточность системы. Согласно этому соотношению, эффективность системы (коэффициент использования канала) полностью определяется величиной ее избыточности, т.е. задача повышения эффективности системы передачи информации сводится к задаче уменьшения избыточности сообщения и сигнала.

Избыточность сообщения обусловлена тем, что элементы сообщения не являются равновероятными и между ними имеется статистическая связь. При кодировании можно перераспределить вероятности исходного сообщения так, чтобы распределение вероятностей символов кода приближалось к оптимальному.

Избыточность сигнала зависит от способа модуляции и вида переносчика. Процесс модуляции обычно сопровождается расширением полосы частот сигнала по сравнению с полосой частот передаваемого сообщения. Это расширение полосы и является избыточным.

Говоря об эффективности системы передачи информации, нельзя забывать о ее помехоустойчивости. Устранение избыточности повышает эффективность передачи, но снижает при этом помехоустойчивость. При кодировании в ряде случаев избыточность вводится специально с целью повышения достоверности передачи. Пример такого кодирования являются корректирующие коды, которые мы рассмотрим позднее.

Таким образом, имеется два основных критерия оценки качества систем передачи информации и наиболее совершенной системой считается такая, которая обеспечивает наибольшую эффективность при заданной помехоустойчивости.