
- •4. Множественная регрессия и корреляция
- •§ 4.1 . Спецификация модели
- •§ 4.2. Отбор факторов при построении множественной регрессии
- •§ 4.3. Выбор формы уравнения регрессии
- •§ 4.4. Оценка параметров уравнения множественной регрессии
- •§ 4.5. Частные уравнения регрессии
- •§ 4.6. Множественная корреляция
- •§ 4.7. Частная корреляция
§ 4.4. Оценка параметров уравнения множественной регрессии
Параметры уравнения множественной регрессии оцениваются, как и в парной регрессии, методом наименьших квадратов (МНК). При его применении строится система нормальных уравнений, решение которой и позволяет получить оценки параметров регрессии.
Так, для уравнения
![]() система нормальных уравнений составит:
система нормальных уравнений составит:
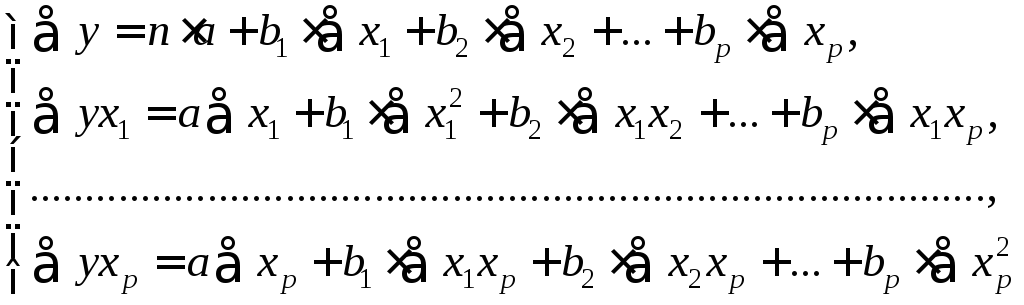
Ее решение может быть осуществлено методом Крамера:
![]() ,
,
![]() ,
…,
,
…,![]() ,
,
где
![]() – определитель системы;
– определитель системы;
![]() –частные
определители.
–частные
определители.
Возможен и иной подход к определению параметров множественной регрессии, когда на основе матрицы парных коэффициентов корреляции строится уравнение регрессии в стандартизованном масштабе:
![]() ,
,
где
![]() – стандартизованные переменные:
– стандартизованные переменные:![]() ,
,![]() ,
,
для которых среднее
значение равно нулю:
![]() ,
а среднее квадратическое отклонение
равно единице:
,
а среднее квадратическое отклонение
равно единице:![]() ;
;
![]() –стандартизованные
коэффициенты регрессии.
–стандартизованные
коэффициенты регрессии.
Применяя МНК к уравнению множественной регрессии в стандартизованном масштабе, после соответствующих преобразований получим систему нормальных уравнений вида
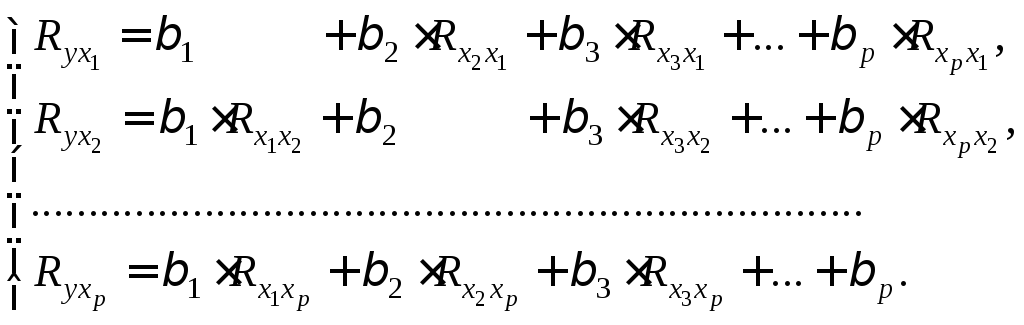
Решая ее методом
определителей, найдем параметры –
стандартизованные коэффициенты регрессии
(![]() -коэффициенты).
-коэффициенты).
Стандартизованные
коэффициенты регрессии показывают, на
сколько сигм изменится в среднем
результат, если соответствующий фактор
![]() изменится на одну сигму при неизменном
среднем уровне других факторов. В силу
того, что все переменные заданы как
центрированные и нормированные,
стандартизованные коэффициенты регрессии
изменится на одну сигму при неизменном
среднем уровне других факторов. В силу
того, что все переменные заданы как
центрированные и нормированные,
стандартизованные коэффициенты регрессии![]() сравнимы между собой. Сравнивая их друг
с другом, можно ранжировать факторы по
силе их воздействия на результат. В этом
основное достоинство стандартизованных
коэффициентов регрессии в отличие от
коэффициентов «чистой» регрессии,
которые несравнимы между собой.
сравнимы между собой. Сравнивая их друг
с другом, можно ранжировать факторы по
силе их воздействия на результат. В этом
основное достоинство стандартизованных
коэффициентов регрессии в отличие от
коэффициентов «чистой» регрессии,
которые несравнимы между собой.
Пример.
Пусть функция издержек производства
![]() (тыс. руб.) характеризуется уравнением
вида
(тыс. руб.) характеризуется уравнением
вида
![]() ,
,
где ![]() основные производственные фонды (тыс.
руб.);
основные производственные фонды (тыс.
руб.);
![]() –численность
занятых в производстве (чел.).
–численность
занятых в производстве (чел.).
Анализируя его,
мы видим, что при той же занятости
дополнительный рост стоимости основных
производственных фондов на 1 тыс. руб.
влечет за собой увеличение затрат в
среднем на 1,2 тыс. руб., а увеличение
численности занятых на одного человека
способствует при той же технической
оснащенности предприятий росту затрат
в среднем на 1,1 тыс. руб. Однако это не
означает, что фактор
![]() ,
оказывает более сильное влияние на
издержки производства по сравнению с
фактором
,
оказывает более сильное влияние на
издержки производства по сравнению с
фактором![]() .
Такое сравнение возможно, если обратиться
к уравнению регрессии в стандартизованном
масштабе. Предположим, оно выглядит
так:
.
Такое сравнение возможно, если обратиться
к уравнению регрессии в стандартизованном
масштабе. Предположим, оно выглядит
так:
![]() .
.
Это означает, что
с ростом фактора
![]() на одну сигму при неизменной численности
занятых затраты на продукцию увеличиваются
в среднем на 0,5 сигмы. Так как
на одну сигму при неизменной численности
занятых затраты на продукцию увеличиваются
в среднем на 0,5 сигмы. Так как![]() (0,5 < 0,8), то можно заключить, что большее
влияние оказывает на производство
продукции фактор
(0,5 < 0,8), то можно заключить, что большее
влияние оказывает на производство
продукции фактор![]() ,
а не
,
а не![]() ;
как кажется из уравнения регрессии в
натуральном масштабе.
;
как кажется из уравнения регрессии в
натуральном масштабе.
В парной зависимости
стандартизованный коэффициент регрессии
есть не что иное, как линейный коэффициент
корреляции
![]() .
Подобно тому, как в парной зависимости
коэффициенты регрессии и корреляции
связаны между собой, так и во множественной
регрессии коэффициенты «чистой»
регрессии
.
Подобно тому, как в парной зависимости
коэффициенты регрессии и корреляции
связаны между собой, так и во множественной
регрессии коэффициенты «чистой»
регрессии![]() связаны со стандартизованными
коэффициентами регрессии
связаны со стандартизованными
коэффициентами регрессии![]() ,
а именно:
,
а именно:
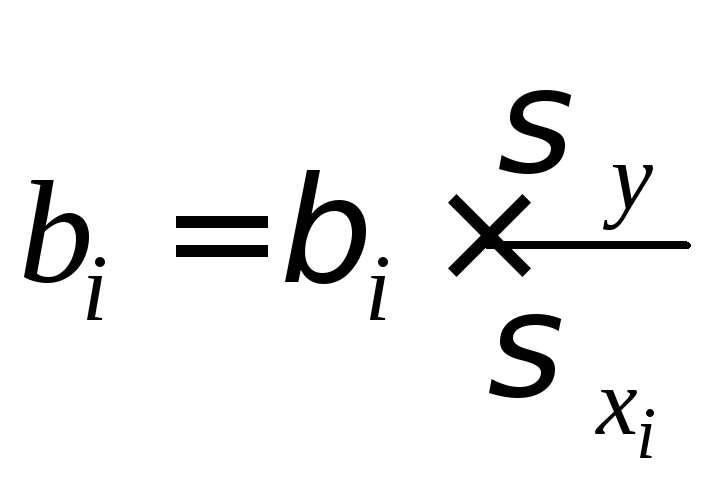 .
.
Это позволяет от уравнения регрессии в стандартизованном масштабе
![]()
переходить к уравнению регрессии в натуральном масштабе переменных:
![]()
Параметр
![]() определяется как
определяется как
![]()
Рассмотренный
смысл стандартизованных коэффициентов
регрессии позволяет их использовать
при отсеве факторов – из модели
исключаются факторы с наименьшим
значением
![]() .
.
Для уравнения
регрессии в стандартизованном масштабе
![]()
![]() -коэффициенты
могут быть определены по формулам,
вытекающим из решения системы нормальных
уравнений:
-коэффициенты
могут быть определены по формулам,
вытекающим из решения системы нормальных
уравнений:
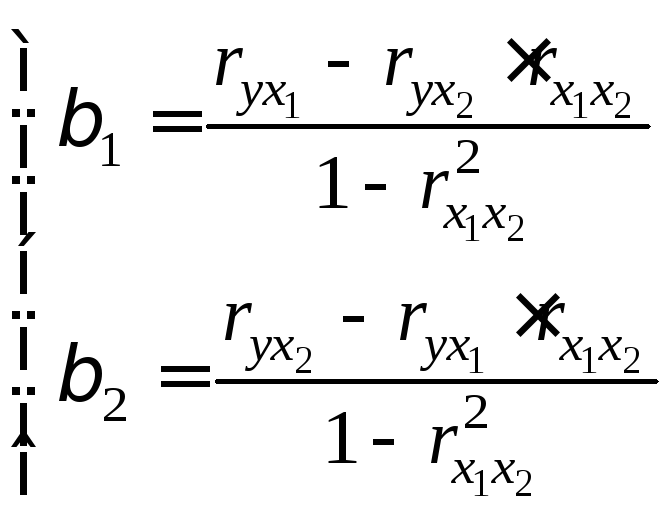
Компьютерные программы построения уравнения множественной регрессии в зависимости от использованного в них алгоритма решения позволяют получить либо только уравнение регрессии для исходных данных, либо, кроме того, уравнение регрессии в стандартизованном масштабе.
При нелинейной зависимости признаков, приводимой к линейному виду, параметры множественной регрессии также определяются МНК с той лишь разницей, что он используется не к исходной информации, а к преобразованным данным.
