3.3 Диаграмма низколегированной стали

Диаграмма растяжения низколегированной стали изображена на рисунке. Аналогичную диаграмму имеют и другие пластичные материалы, например красная медь, сплавы алюминия.

В начале диаграммы между нагрузкой и деформацией тоже соблюдается прямо пропорциональная зависимость (закон Гука). Точка, где эта зависимость нарушается, соответствует пределу пропорциональности. После точки А прямолинейный участок диаграммы плавно переходит в криволинейный – зону пластических деформаций.

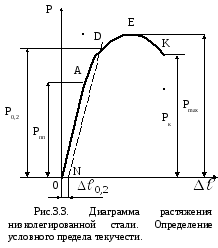
На диаграмме растяжения нет площадки текучести. Поэтому вместо физического предела текучести определяют условный предел текучести (точка D на рис. 3.3) – напряжение, при котором остаточное удлинение достигает 0,2% от рабочей длины образца:

. (3.7)

Для определения нагрузки Р_0,2 вычисляется значение заданного остаточного удлинения 0,2 % исходя из рабочей длины образца. Отрезок, соответствующий остаточной деформации АД, откладываем вправо от точки О (на рис.3.3 — отрезок ON). Из точки N проводится прямая, параллельная прямой ОА, до пересечения с диаграммой растяжения. Ордината точки пересечения D равна нагрузке P_0,2.

3.4 Диаграмма растяжения чугуна

Диаграмма растяжения чугуна, изображенная на рис. 3.4, является типичной для хрупких материалов. Диаграмма не имеет прямолинейного участка, так как упругие деформации не пропорциональны нагрузкам даже при небольших напряжениях. Нагрузка плавно увеличивается до наибольшего значения (точка Е). Напряжения при нагрузке P_max соответствуют пределу прочности . После точкиЕ без уменьшения нагрузки происходит разрыв образца. Образец разрушается при весьма незначительном удлинении и без образования шейки. Остаточные деформации очень малы, обычно менее 1% от расчетной длины образца.

Характер разрушения чугунного существенно отличается от разрушения стального образца. Разрушение чугунного образца происходит в результате отрыва по площадке, перпендикулярной направлению растягивающей силы. На поверхности излома видна крупнозернистая структура материала.

3.5 Допускаемые напряжения

Размеры деталей при инженерном расчете необходимо подбирать таким образом, чтобы под действием приложенных нагрузок элемент конструкции не разрушался и не получал деформаций, превышающих допустимые.

Как показывают механические испытания разрушение хрупких материалов начинается, когда напряжения в сечении элемента конструкции превысят величину временного сопротивления (предела прочности) . Поэтому для хрупких материалов, деформация которых, как правило, незначительна, за опасное (предельное) напряжение принимают именно предел прочности.

Для пластичных материалов опасным является предел текучести (или условный предел текучести, если отсутствует площадка текучести), так как за пределом текучести в пластичных материалах возникают значительные пластические деформации, приводящие при сбросе нагрузки до нуля к появлению остаточных напряжений.

Естественно, что эти напряжения не могут быть использованы в качестве допускаемых. Их следует уменьшить настолько, чтобы в эксплуатационных условиях действующие напряжения гарантированно были меньше опасных, деформации были упругими для этого выбирают коэффициент запаса прочности.

Допускаемые напряжения – это наибольшие напряжения, которые можно допустить в конструкции при условии его безопасной, надежной и долговечной работы.

Выбор коэффициента запаса прочности зависит:

- состояния материала (хрупкий, пластичный);

- характера нагрузки (статическая, динамическая или переменная);

- неточности задания величины внешней нагрузки;

- неточности расчетных схем и приближенности методов расчета;

- значимости проектируемого сооружения или конструкции и т.д.

Для пластичных материалов (конструкционных сталей) значение коэффициента запаса прочности принимается .