1.1. Краткие сведения из теории

Синтез (проектирование) новой машины начинается с составления кинематической схемы ее механизмов. Основными структурными элементами механизма являются звенья и кинематические пары.

Звено механизма – это одно или несколько жестко соединенных тел. Они имеют различное конструктивное оформление в зависимости от назначения. Неподвижное звено называется стойкой. У предложенных моделей стойкой считается панель, на которой собран механизм. Звенья соединяются между собой подвижно. Подвижное соединение двух звеньев, допускающее их относительное движение, называется кинематической парой.

Кинематическая цепь – это связанная система звеньев, образующих между собой кинематические пары. Цепи могут быть простыми (рис. 1.1,а,в), сложными (рис. 1.1,б), замкнутыми (рис. 1.1,в), незамкнутыми (рис. 1.1,а,б). Кроме того, цепи могут быть плоскими (когда все точки звеньев перемещаются в одной или в параллельных плоскостях) и пространственными (точки звеньев описывают неплоские траектории).

Механизмом является только такая кинематическая цепь, в которой при заданном движении одного или нескольких ведущих звеньев относительно неподвижного звена (стойки, панели механизма) все остальные ведомые звенья совершают определенные движения.

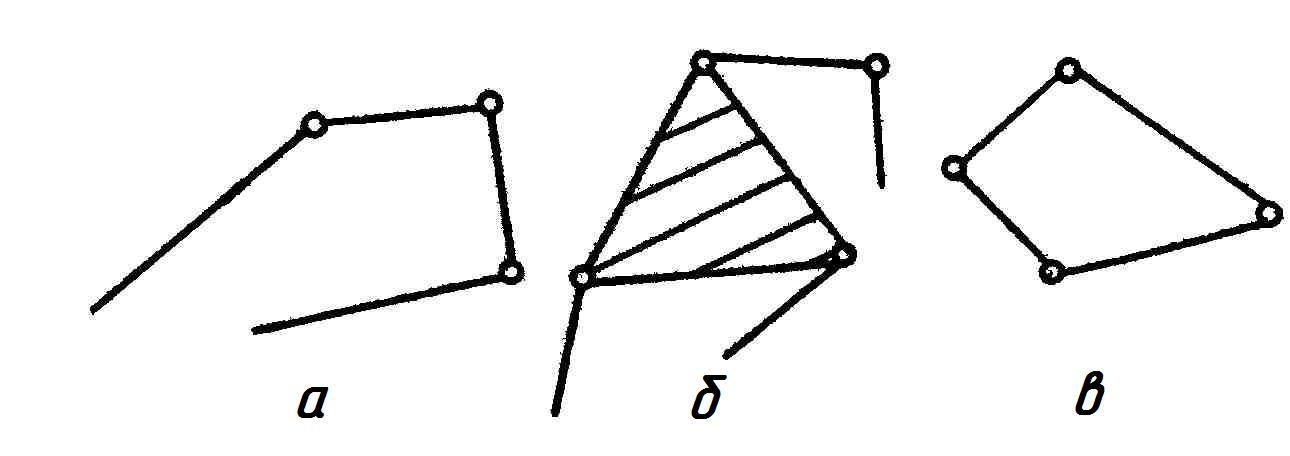
Рис. 1.1

Ведущим называется звено, к которому приложена движущая сила или момент сил, закон движения которого известен. На схемах ведущие звенья обозначаются стрелкой.

В рычажных механизмах вращающиеся на полный оборот звенья называются кривошипами, качающиеся – коромыслами, совершающие плоскопараллельные движения – шатунами, движущиеся поступательно – ползунами.

При проектировании новых или исследовании существующих механизмов следует определить степень подвижности – число, соответствующее количеству ведущих звеньев механизма.

Для плоской кинематической цепи степень подвижности определяется по формуле Чебышева:

, (1.1)

где n – общее количество звеньев, включая стойку;

p₅ и p₄ – количество кинематических пар пятого и четвертого класса;

2, 1 – количество ограничений движений (условий связи), накладываемых на относительные движения звеньев в парах пятого и четвертого класса соответственно;

3 – число степеней свободы каждого звена на плоскости;

3^* – число степеней свободы стойки (панели) как самостоятельного звена на плоскости.

Если при подсчете звеньев стойку не учитывать, то формула Чебышева будет иметь вид:

, (1.2)

где K – количество подвижных звеньев.

Определение степени подвижности механизма можно выполнять любым способом, используя формулы (1.1) или (1.2). Поясним на примерах: по формуле (1.1) – смотри пример 1, по формуле (1.2) – смотри пример 2.

П р и м е р 1. Определить число ведущих звеньев заданного механизма (рис.1.2,а). В точке контакта Р₄ зубчатых колес Z₁ и Z₂ кинематическая пара четвертого класса, все остальные – пятого.

В этом механизме одно ведущее звено Z₁.

П р и м е р 2. Определить число ведущих звеньев заданного механизма (рис.1.2,б). Здесь нет кинематических пар четвертого класса. В точке Д следует рассмотреть соединение звеньев 4 и 5 вращательной (VI) кинематической парой, а звеньев 5 и 6 (опора) – поступательной (VII).

За ведущее звено рекомендуется принять звено 1 – кривошип.

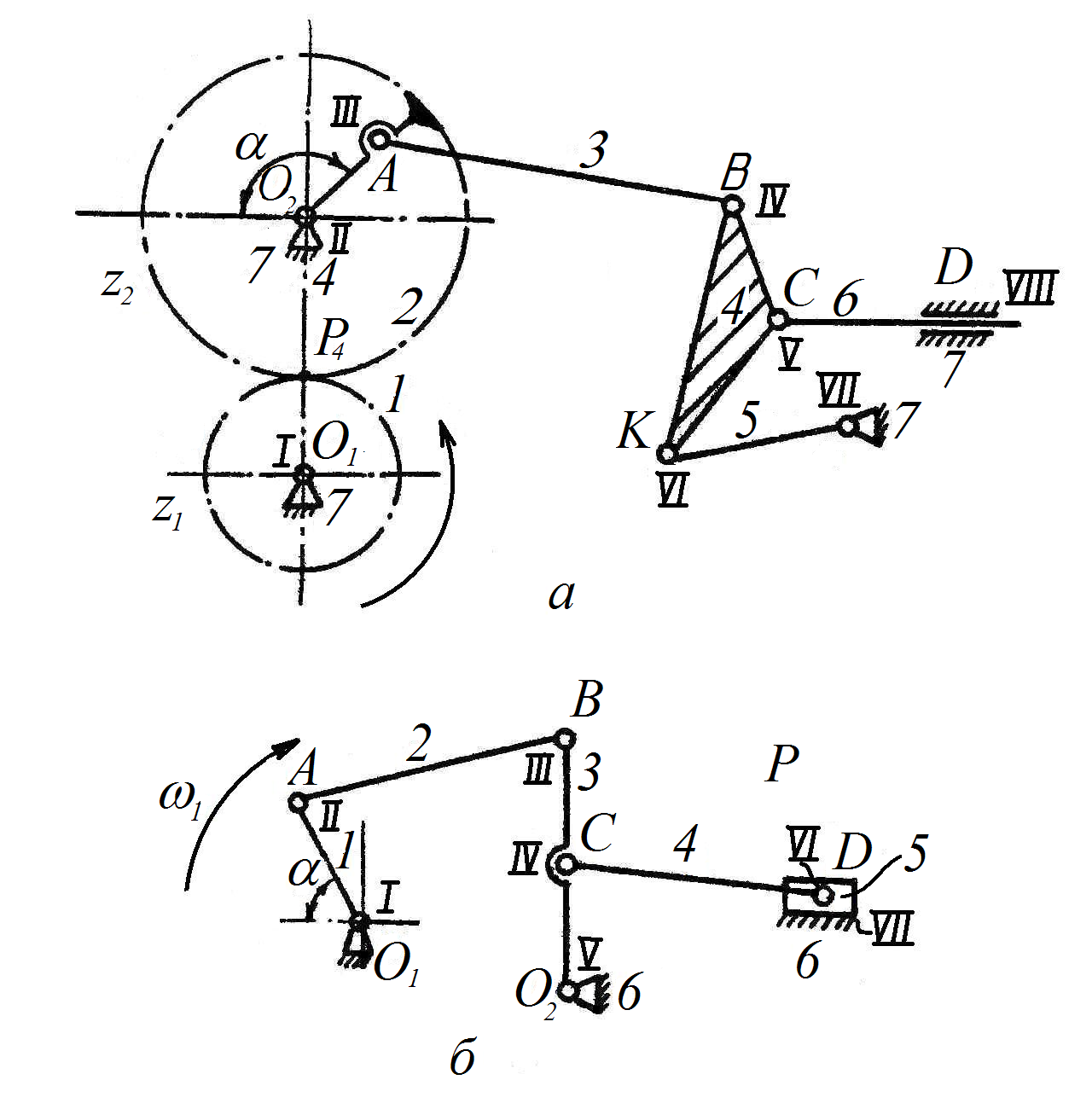
Рис. 1.2

При выполнении работы следует иметь в виду, что в некоторых механизмах могут встретиться звенья и кинематические пары, которые не влияют на характер движения механизма в целом, а вводятся для передачи движения какой-либо точки механизма на расстояние или для придания жесткости системе. На схеме рычажного механизма (рис. 1.3,а), исключив звено 5 вместе с кинематическими парами II и V (характер работы звеньев 1–3 не нарушится), получим действительную величину подвижности:

После удаления из расчета звена 5 и кинематических пар II и V

На схеме кулачкового механизма (рис. 1.3,б) ролик 2 входит во вращательную пару пятого класса со звеном 3 и в пару четвертого класса со звеном 1. Ролик можно свободно проворачивать вокруг оси О₂, не влияя на характер движения звена 3. Ролик 2 при этом дает лишнюю степень свободы, и если его убрать, соединив звено 3 со звеном 1, характер работы звеньев механизма не нарушится, т. е.

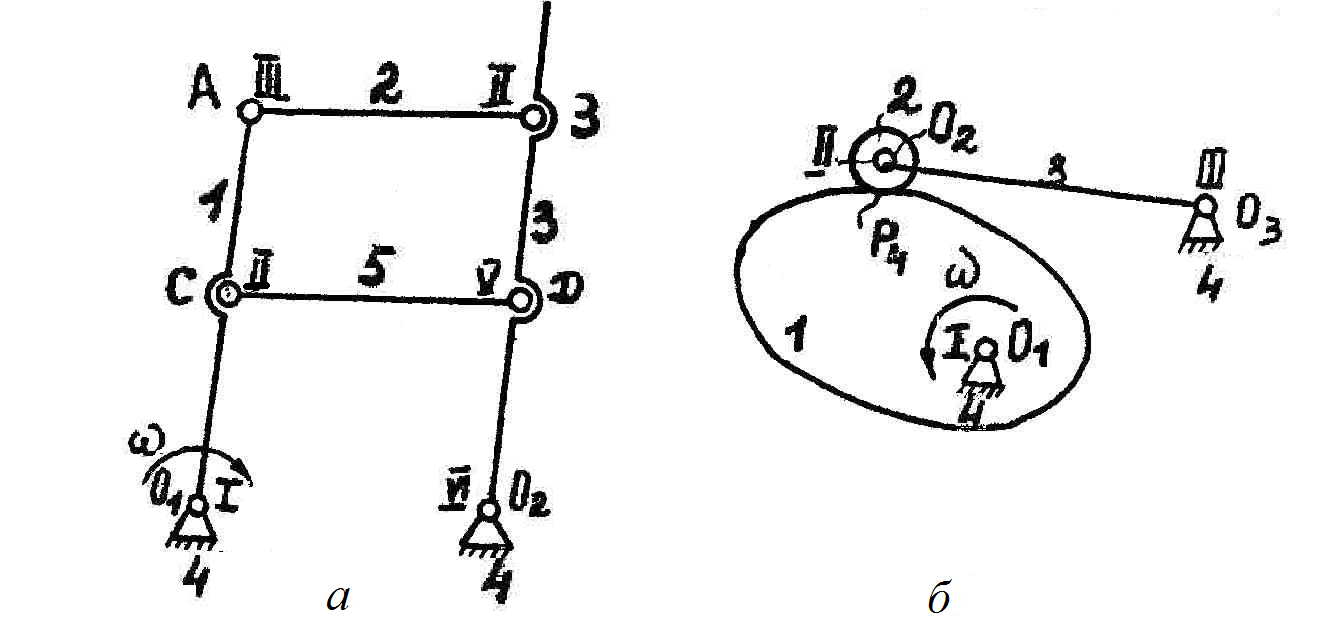
Рис. 1.3

После удаления ролика 2 из схемы

При изучении структуры и кинематики механизмов с высшими парами удобно заменять их на низшие. При этом должно соблюдаться условие структурной эквивалентности, т. е. должна сократиться степень подвижности и не должен изменяться характер мгновенного относительного движения всех звеньев механизма. Порядок замены следующий:

1. вместо высшей пары вводят условное звено, входящее в две вращательные пары;

2. центры вращательных пар помещают в центрах кривизны профилей, образующих высшую пару;

3. вновь введенными низшими (вращательными) парами соединяют условное звено с теми звеньями, которые входили в высшую пару.

Схемы некоторых механизмов приведены в табл. 1.1.

Рис. 1.4

Классификация плоских механизмов по Ассуру позволяет для механизмов одного класса применить методику кинематического и силового анализа, разработанную для этого класса. По классификации Ассура простейший двухзвенный механизм, состоящий из стойки О и кривошипа 1 (рис. 1.4), соединенных одной низшей кинематической парой I, называется механизмом I класса.

Любой более сложный механизм образуется последовательным присоединением к нему кинематических цепей, у которых Такие цепи называются группами Ассура. Поскольку для группы Ассура

(1.3)

то присоединение такой группы к звеньям какой-либо кинематической цепи не изменит степени подвижности этой цепи. Из уравнения (1.3) получим зависимость числа пар (р₅) от числа звеньев (n) группы Ассура:

. (1.4)

Т а б л и ц а 1.1

Схемы заменяющих механизмов

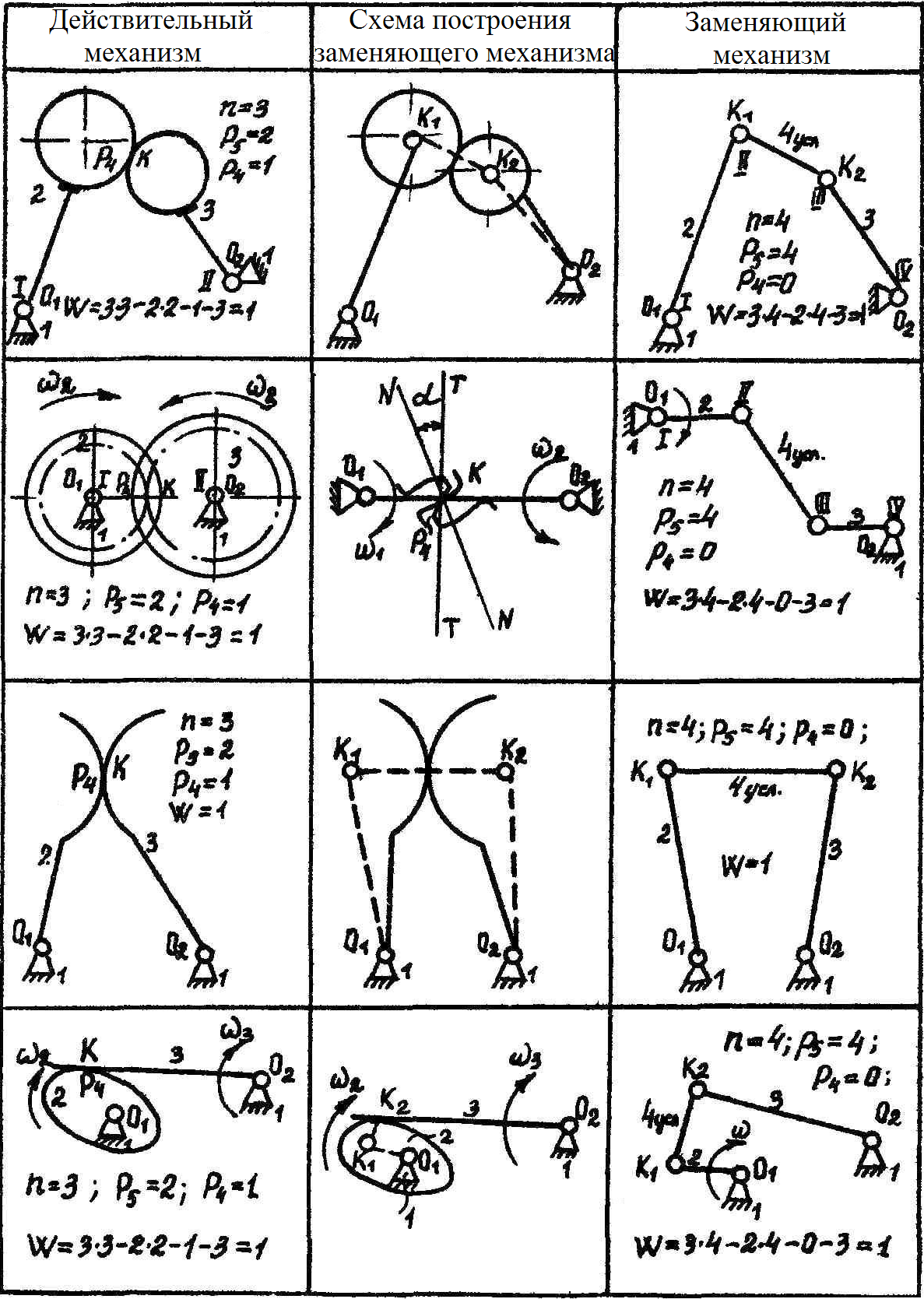
Таким образом, в группах Ассура могут быть сочетания чисел звеньев и кинематических пар пятого класса, приведенные в табл. 1.2.

Т а б л и ц а 1.2

Сочетания чисел звеньев (n) и кинематических пар (p₅)

n	2	4	6	9	…
p5	3	6	9	12	…

Во втором столбце табл. 1.2 приведены сочетания групп Ассура второго класса различных видов (рис. 1.5,а).

2-й класс: п = 2; Р = 3; W = 0

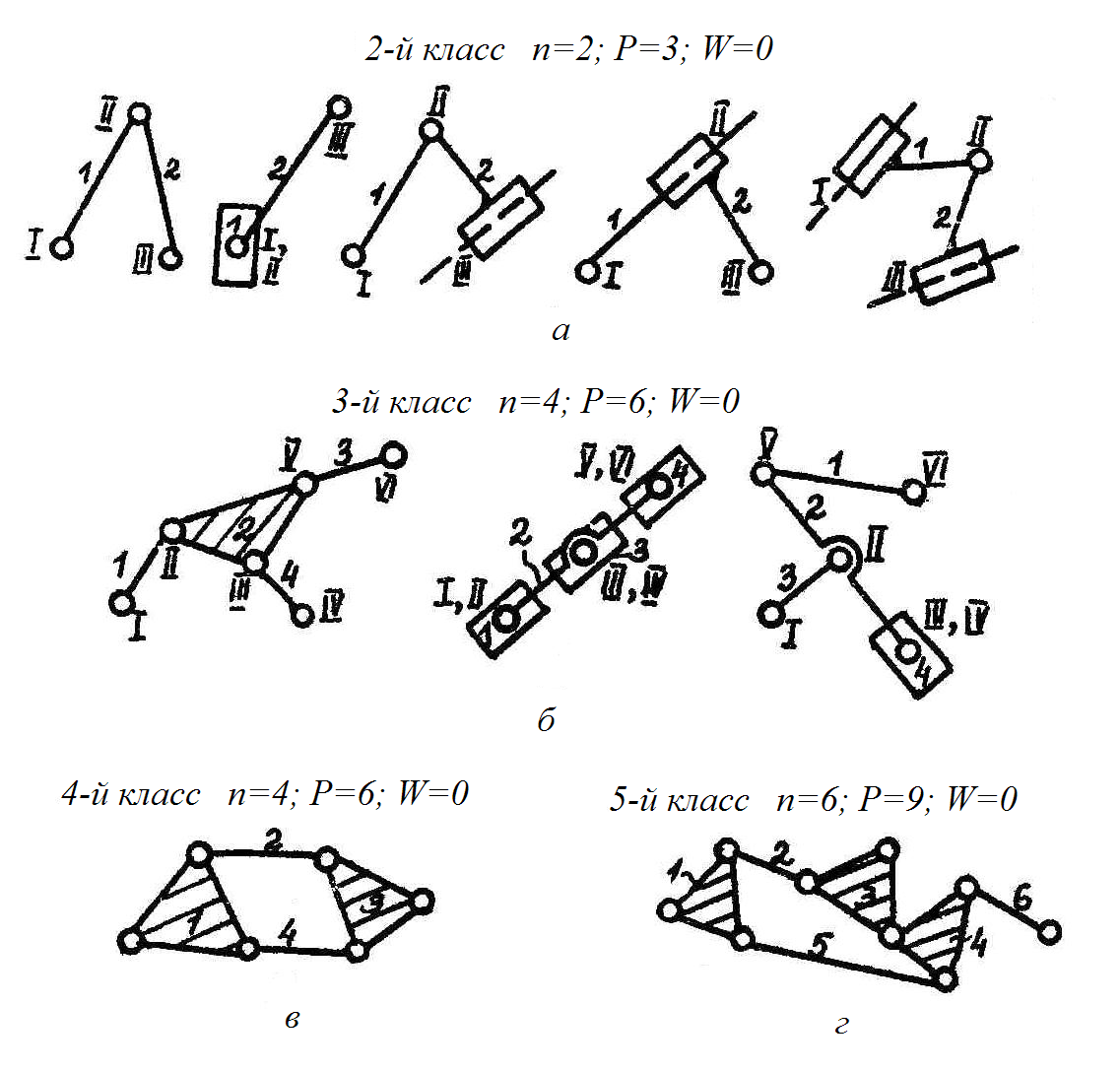
3-й класс: п = 4; Р = 6; W = 0

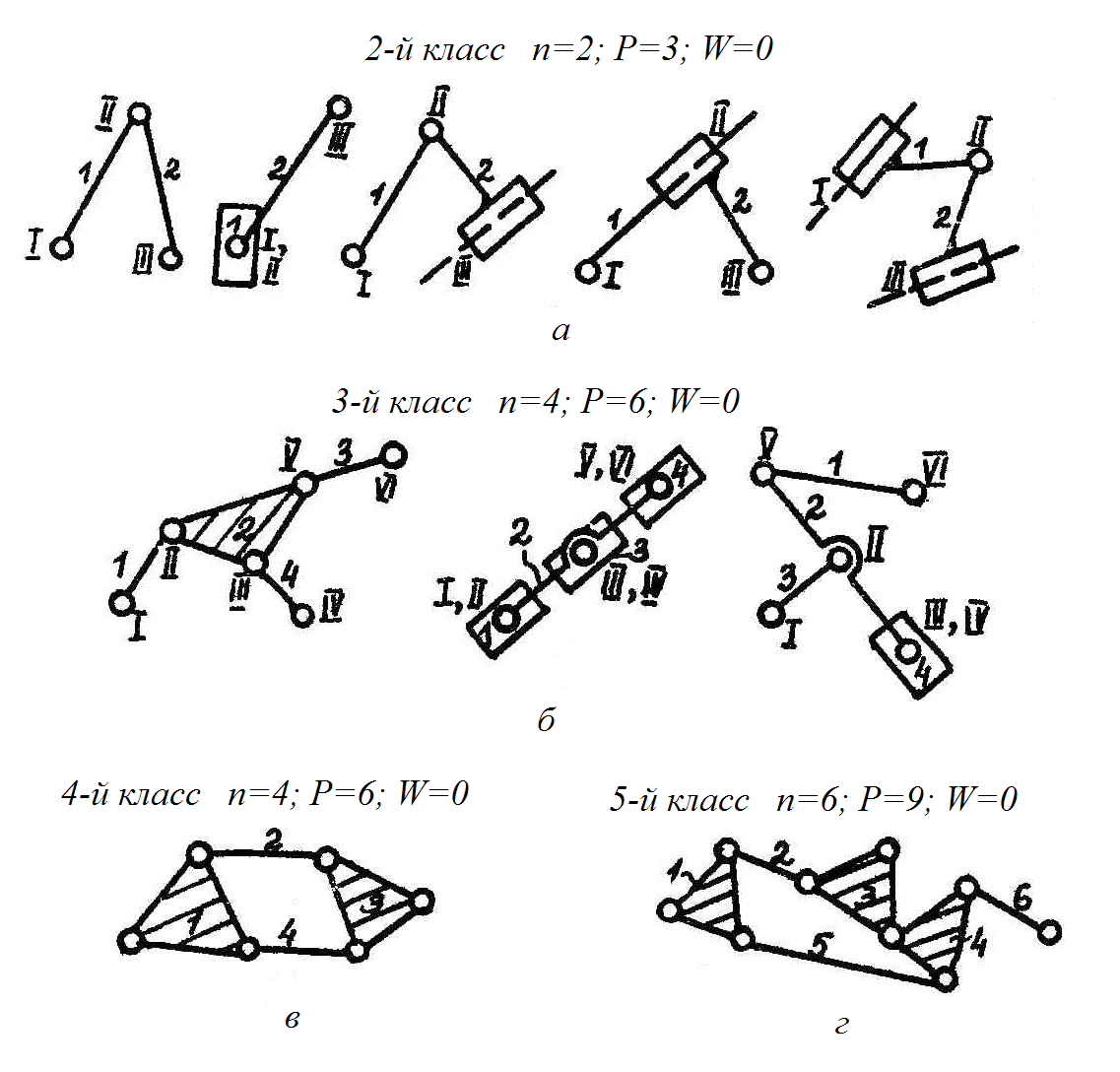
4-й класс: п = 4; Р = 6; W = 0 5-й класс: п = 6; Р = 9; W = 0

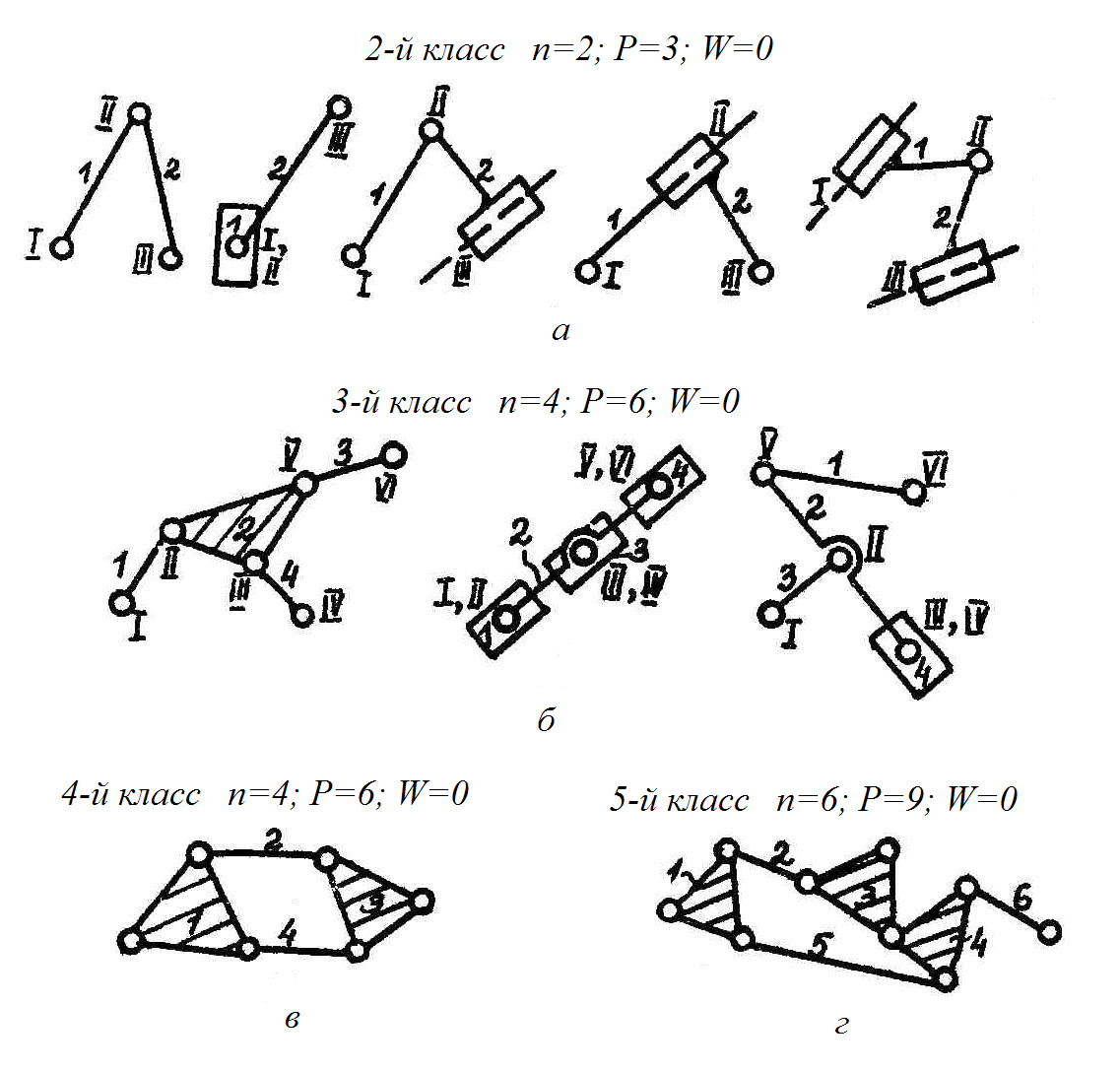
Рис. 1.5

Цифры из второго столбца табл. 1.2 позволяют определить группу третьего класса (рис. 1.5,б).

Класс группы Ассура выше третьего определяется числом внутренних кинематических пар, образующих так называемый наиболее сложный замкнутый контур (рис. 1.5,в – четвертый класс, г – пятый).

Класс механизма определяется наивысшим классом группы Ассура, которая входит в его состав.

Для правильного определения класса механизма необходимо

рассчитать подвижность механизма W;

отсоединить наиболее удаленную от ведущего звена группу Ассура II класса и проверить подвижность оставшегося механизма. Если подвижность изменилась, то отсоединение сделано неправильно: возможно, отсоединять надо группу III класса;

отделение групп производить до тех пор, пока не останется одно ведущее звено со стойкой;

на основании разложения механизма на группы Ассура написать формулу строения механизма в порядке присоединения групп к ведущему звену и стойке.

Например:

для механизма, представленного на рис. 1.2,а, – [2] → [3, 4, 5, 6]; (1.5)

б – [1] → [2, 3] → [4, 5]. (1.6)

В первых квадратных скобках указаны номера ведущих звеньев, в последующих – номера звеньев, входящих в группы Ассура соответствующего класса.