2. Электростатика

2.1. Краткие теоретические сведения

Электростатика изучает электрическое поле, которое создается неподвижными относительно данной системы отсчета электрическими зарядами. Любой электрический заряд q в природе квантуется, т. е. кратен элементарному заряду е:

q = Ne, (1)

где N = 1, 2, 3, …; е = 1,610^19 Кл.

В замкнутой системе выполняется закон сохранения заряда:

q₁ + q₂ + q₃ + … + q_n = const. (2)

Сила взаимодействия двух неподвижных точечных зарядов в вакууме определяется по закону Кулона:

F = , (3)

где 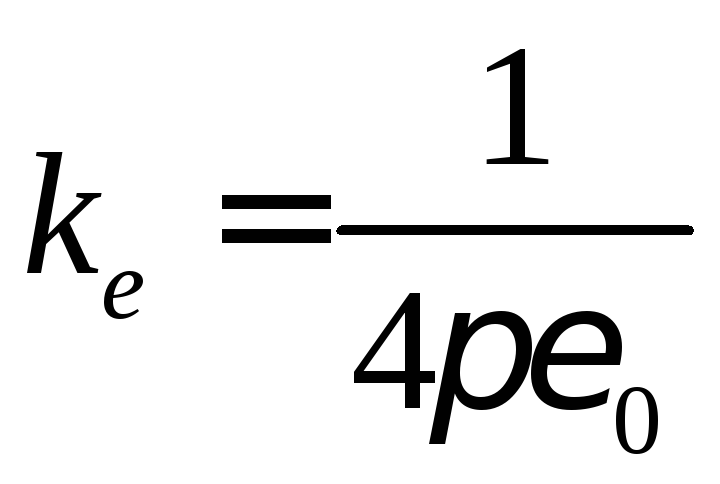= 910⁹ , здесь 8,8510^12 ;

r – расстояние между зарядами.

Закон Кулона для взаимодействия зарядов в среде имеет вид:

F = 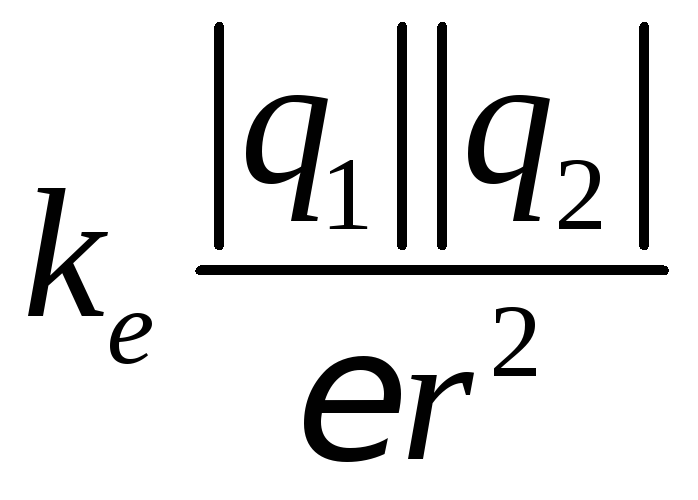, (4)

где   диэлектрическая проницаемость среды.

При взаимодействии нескольких зарядов силы взаимодействия каждой пары зарядов не зависят от наличия остальных зарядов, поэтому сила действующая на каждый заряд, равна векторной сумме сил , действующих на него со стороны всех других зарядов (принцип суперпозиции сил):

. (5)

Силовой характеристикой электростатического поля является напряженность:

= . (6)

Модуль напряженности электростатического поля точечного заряда (в вакууме 1) рассчитывается по формуле:

Е = 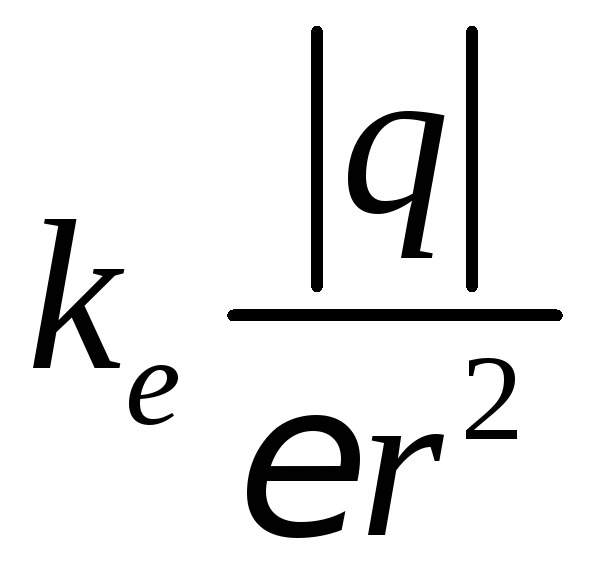, (7)

где r – расстояние от заряда до точки, в которой определяется напряженность поля.

Модуль напряженности электростатического поля заряженной сферы радиуса R определяется по уравнению:

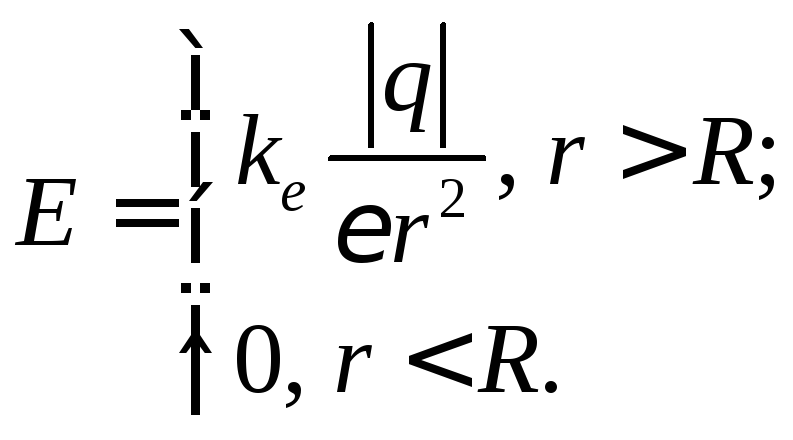(8)

Модуль напряженности бесконечной заряженной плоскости с любой стороны вычисляется по выражению:

2k_e| |, (9)

где   поверхностная плотность заряда плоскости.

Модуль напряженности двух заряженных плоскостей

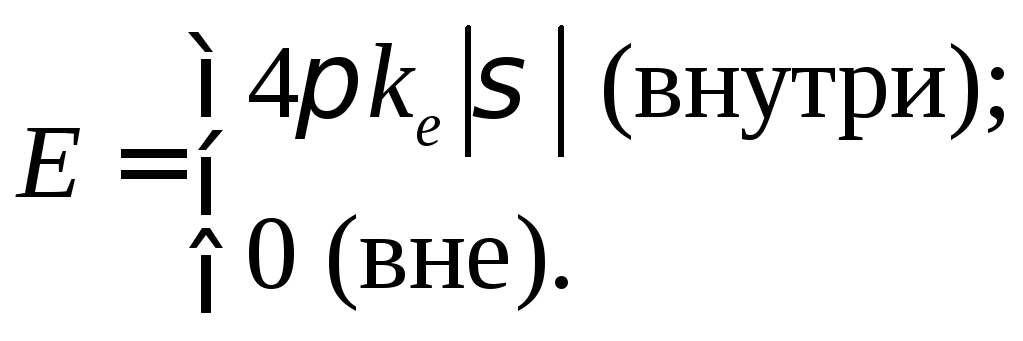(10)

Модуль напряженности электростатического поля бесконечно длинной заряженной нити (вне нити):

, (11)

где   линейная плотность заряда нити;

r – расстояние от нити до точки, в которой определяется напряженность поля.

Если поле создано несколькими точечными зарядами, то согласно принципу суперпозиции полей напряженность в каждой точке поля равна векторной сумме напряженностей полей , создаваемых каждым зарядом в отдельности:

. (12)

В случае, когда поле создано не точечными зарядами, а распределенными симметрично по сферическим, цилиндрическим и плоским поверхностям, напряженность поля рассчитывают с помощью теоремы Гаусса.

Поток вектора напряженности электрического поля _е  через заданную поверхность пропорционален алгебраической сумме зарядов q_i, находящихся внутри этой поверхности:



S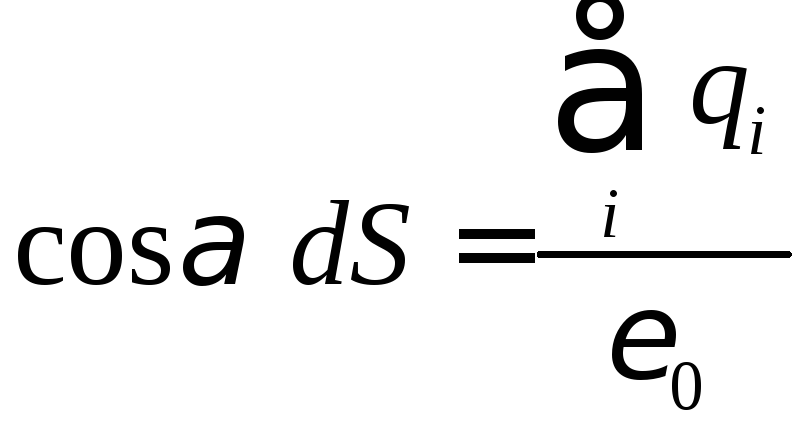

_е =∮Е. (13)

Энергетической характеристикой электростатического поля является потенциал  :

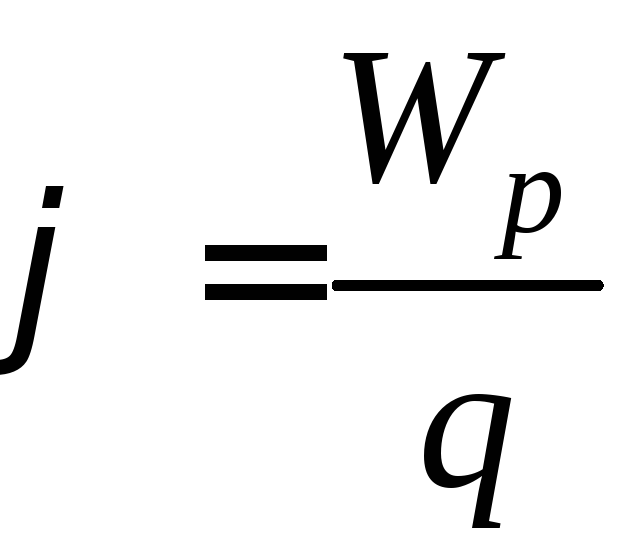, (14)

где W_p  потенциальная энергия.

Потенциал точечного заряда определяется по формуле (с точностью до константы):

, (15)

где r – расстояние от заряда до точки, в которой определяют потенциал поля.

Потенциал электростатического поля заряженной сферы радиуса R

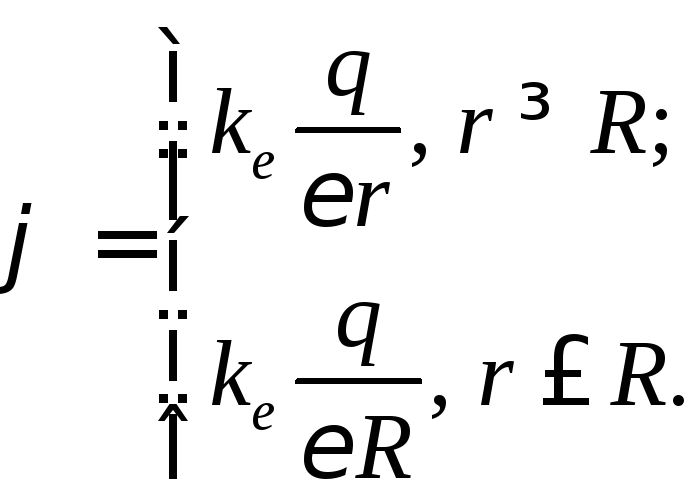(16)

При расчете потенциала полей, создаваемых системой зарядов, следует применять принцип суперпозиции: результирующий потенциал  в каждой точке поля равен алгебраической сумме потенциалов _i полей, созданных отдельными зарядами:

. (17)

Между двумя характеристиками электростатического поля – напряженностью и потенциалом – существует определенная связь: дифференциальная и интегральная:

(18)

. (19)

Следует понимать, что формула

, (20)

где d – модуль перемещения;

 – угол между вектором перемещения и вектором ,

справедлива только для однородного поля.

Перемещение заряда под действием электрического поля происходит в сторону убывания потенциальной энергии. Работа по перемещению заряда на основании закона сохранения энергии равна уменьшению потенциальной энергии W_p:

A = W_p = . (21)

Электроемкость проводника С численно равна заряду, изменяющему его потенциал на единицу, и зависит от геометрических характеристик проводника и диэлектрических свойств среды.

Для шара электроемкость определяется через его радиус R и диэлектрическую проницаемость окружающей среды  :

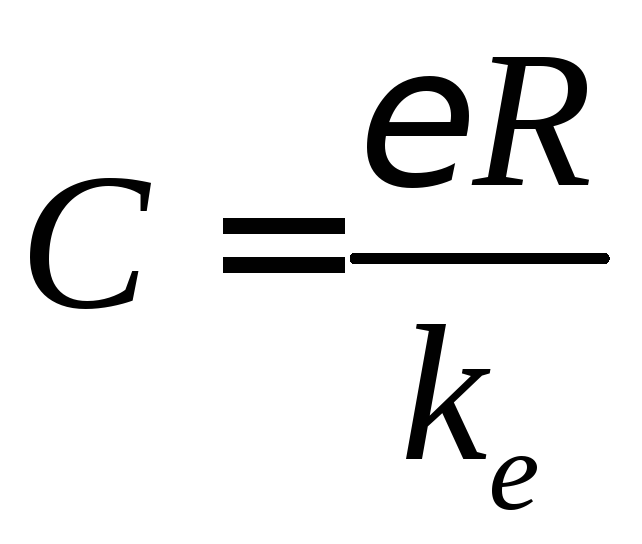. (22)

Электроемкость плоского конденсатора определяется площадью пластин S, расстоянием d между ними и диэлектрическими свойствами среды между пластинами:

(23)

При параллельном соединении конденсаторов выполняются следующие соотношения для их электроемкости С, зарядов на пластинах q и напряжения между пластинами:

;

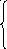; (24)

;

при последовательном соединении 

;

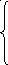; (25)

.

Диэлектрическая проницаемость вещества  показывает, во сколько раз напряженность электростатического поля в вакууме Е₀ больше напряженности электростатического поля в веществе Е:

. (26)

Электростатическую индукцию поля можно рассчитать через характе-ристики поля в вакууме или в веществе:

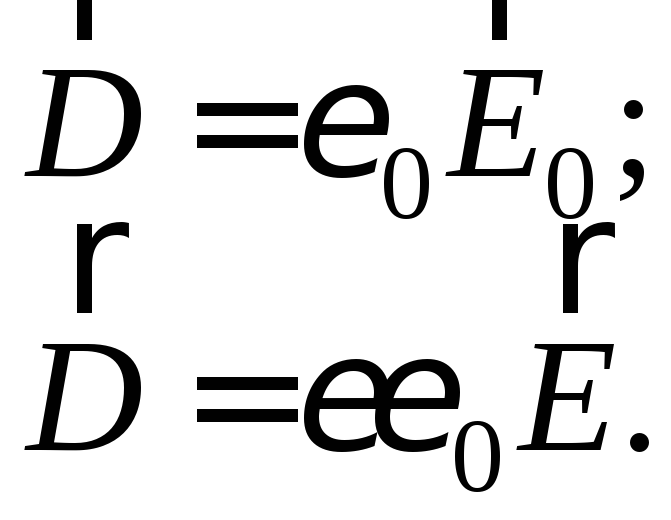(27)