
- •1. Технические требования
- •1.1. Материалы и чертежный инструмент
- •1.2. Некоторые приемы выполнения графических изображений
- •2. Уклоны и конусность
- •2.1. Уклоны
- •2.2. Конусность
- •3. Сопряжение линий
- •3.1. Общие положения
- •3.2. Построение касательных
- •3.3. Сопряжение двух прямых
- •3.4. Сопряжение прямой с окружностью (внутреннее и внешнее)
- •3.5. Сопряжение двух окружностей
- •4. Порядок построения профиля рельсов
- •4.1. Построение профиля кранового рельса
- •4.2. Построение профиля железнодорожного рельса
- •4.3. Построение профиля острякового рельса
- •Задания для выполнения контрольной графической работы
- •644046, Г. Омск, пр. Маркса, 35
2. Уклоны и конусность
2.1. Уклоны
Уклоном прямой по отношению к какой-либо другой прямой называется
величина наклона первой прямой ко второй, которая выражается отношением длины противолежащего катета прямоугольного треугольника к длине прилежащего (рис. 2.1).
Уклон
выражается в процентном и арифметическом
выражениях.
Например, требуется построить уклон 1 : 2. Для этого по горизонтальной
линии необходимо отложить два раза длину произвольного отрезка, получится отрезок общей длиной а, по вертикальной – одну длину отрезка, получится отрезок длиной b, тогда уклон в арифметическом выражении будет иметь вид:
I = b/a = tg . (2.1)
На чертеже перед размерным числом, определяющим величину уклона, ставят знак , острый угол которого направлен в сторону уклона.
2.2. Конусность
Конусность – отношение диаметра D основания конуса к его высоте l0
(рис. 2.2):
K = D/ l0. (2.2)
D: l0
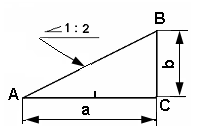
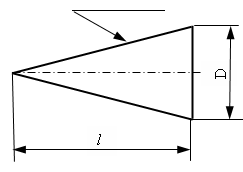
Рис. 2.1. Уклон 1: 2
Рис. 2.2. Конусность
D :
l0
Если рассматривается усеченный конус, то конусность определяется де- лением разности диаметров оснований конуса на расстояние между ними
(рис. 2.3, б):
К = (D – d)/l, (2.3)
где К – конусность;
D, d – диаметры большего и меньшего оснований конуса;
l – высота усеченного конуса.
Например, необходимо построить конусность 1: 2.
Для этого строим
конус (рис. 2.3, а), у которого высота в
два раза больше диаметра основания
(l0
= 2, D
= 1).
Рис. 2.3
.
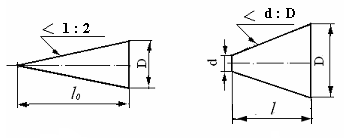
а б
Рис. 2.3. Построение
конусности
Т а б л и ц а 2.1
Значения углов конуса
-
Конусность
Угол конуса
Конусность
Угол конуса
1: 5
1 : 7
1 : 10
11 25 16
8 10 16
5 43 29
1: 15
1 : 20
1: 50
3 4906
2 51 51
1 8 45
3. Сопряжение линий
3.1. Общие положения
Сопряжением называют плавный переход из одной линии в другую. В тео-
рии сопряжения применяют следующие термины: центр сопряжения – точка О; радиус сопряжения – Rс; точки сопряже-
н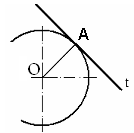 ия
– А и В. Для выполнения сопряжения
ия
– А и В. Для выполнения сопряжения
определяют три элемента: радиус сопряже-
ния; центр сопряжения; точки сопряжения.
Как правило, в заданиях предложен один из
перечисленных выше элементов, другие
находят. Построение сопряжения основано
на следующих положениях геометрии:
при сопряжении прямой линии
с дугой окружности прямая является каса-
т
Рис. 3.1. Сопряжение
прямой линии с дугой
окружности
ния лежит на перпендикуляре, опущенном
из центра окружности О на касательную
(рис. 3.1);
2) при сопряжении двух окружностей точка сопряжения принадлежит общей касательной к обеим окружностям и находится на прямой, соединяющей данные окружности (рис. 3.2);
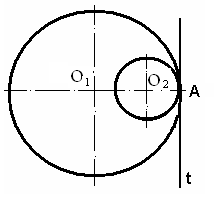
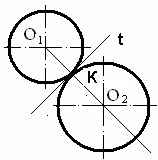
а б
Рис. 3.2. Сопряжения двух окружностей
3) при внешнем касании окружностей (центры окружностей лежат по
разные стороны от общей касательной) расстояние между центрами окруж-
ностей равно сумме радиусов, а при внутреннем (центры окружностей находятся по одну сторону от касательной) – разности их радиусов (рис. 3.2, б);
4) центр дуги сопряжения определяется пересечением линий, проведенных на расстоянии радиуса сопряжения от сопрягаемых линий;
5) через точку сопряжения проходят касательная и нормаль к сопрягаемым линиям.
