7. Интегрирование тригонометрических функций

Интегралы вида , где - рациональная функция, приводятся к интегралам от рациональных дробей с помощью следующих подстановок:

1) универсальная тригонометрическая подстановка . Она часто приводит к громоздким вычислениям. Поэтому в ряде случаев применяют более удобные подстановки:

2) , если , т.е. подынтегральная функция нечетная относительно ;

3) , если , т.е. подынтегральная функция нечетная относительно ;

4) , если , т.е. подынтегральная функция четная относительно и .

Для удобства сведем эти подстановки в табл. 2.

Таблица 2

Таблица тригонометрических подстановок

Интегралы вида при нечетных или вычисляется с помощью подстановки 2 или 3. Если и четны, то можно воспользоваться подстановкой 4. Однако, если и неотрицательны, то эта подстановка приводит к громоздким вычислениям. В этом случае применяются следующие формулы понижения степени:

; (15) ; (16) ; (17)

; (18) ; (19)

. (20)

Формулы (18)-(20) используются также для интегрирования произведений тригонометрических функций с различными аргументами.

Примеры

1) . Подынтегральная функция рационально зависит от и , поэтому

применим подстановку . Выражения для , и через возьмем из табл. 2.

.

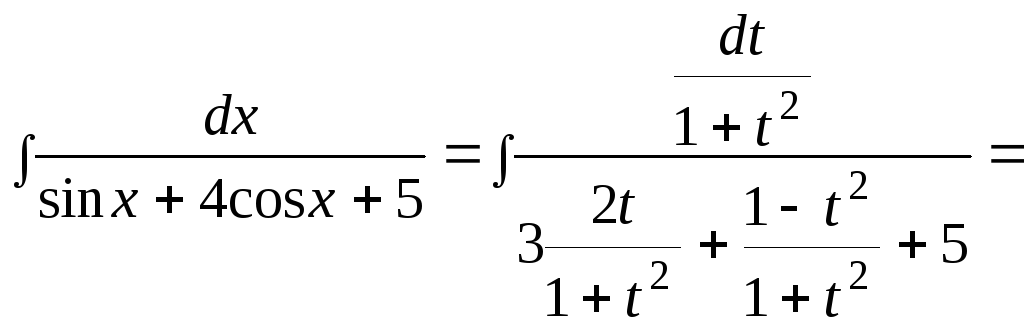
2) . Перепишем подынтегральное выражение следующим образом: 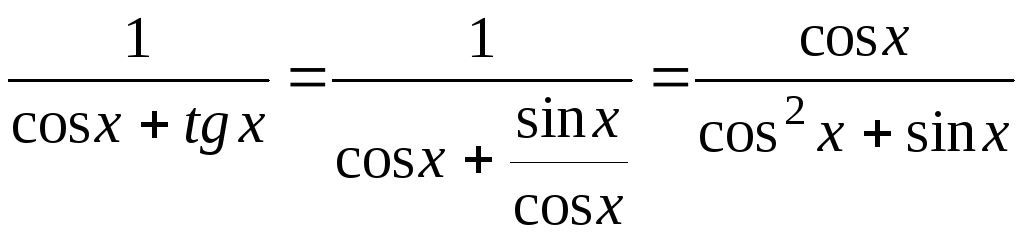. Легко увидеть, что подынтегральное выражение нечетное относительно . Поэтому применяем подстановку :

.

3) . Здесь - нечетное число, поэтому далее делаем подстановку :

.

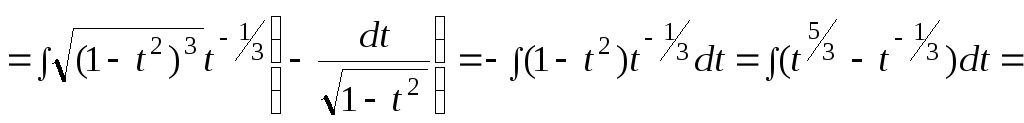
4) . Подынтегральное выражение четно как относительно , так и , поэтому применяем подстановку :

.

5) . Здесь - четные неотрицательные числа. Воспользуемся формулами понижения степени и (15)-(17) за счет удвоения угла:

.

6) . Воспользуемся формулой (4).

.

8. Интегрирование иррациональных функций

Интегралы вида , где означает рациональную функцию от двух аргументов; - натуральные числа; - постоянные. Указанный интеграл преобразуется в интеграл от рациональной функции заменой или , откуда и .

И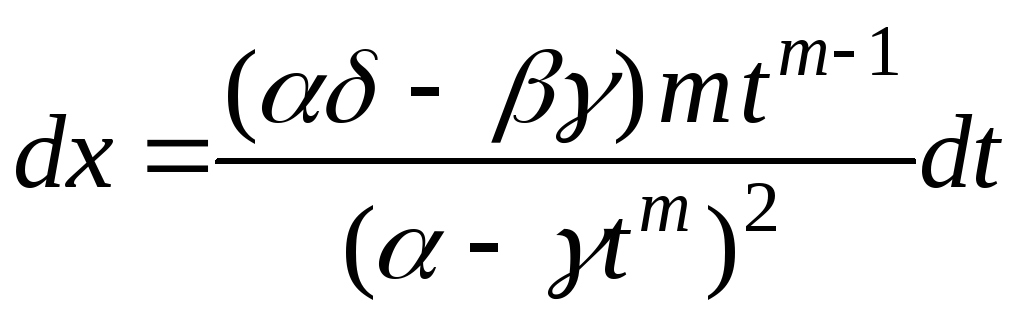нтегралы вида где - рациональная функция; - целые числа. Указанный интеграл преобразуется в интеграл от рациональной функции с помощью подстановки , где - наименьшее общее кратное чисел (общий знаменатель дробей ), отсюда .

Интегралы вида , где - рациональная функция. Подстановка преобразует интеграл к одному из следующих трех типов (см. табл.3).

Таблица 3

Таблица иррациональных подстановок

Вид подынтегрального выражения

Подстановками из табл. 3 эти интегралы соответственно приводятся к интегралам вида .

О других способах вычисления интегралов данного вида см. в [2] и [3].

Интегралы от биномиальных дифференциалов имеют вид: , где - любые постоянные, не равные нулю; - рациональные числа; - несократимые дроби. Интеграл выражается через элементарные функции только в трех случаях, сведенных в табл. 4.

Таблица 4

Таблица интегрирования биномиальных дифференциалов

Характеристика случая	Замена		t	dx
целое	, где
целое
целое

Примеры

1) . К цели приводит замена . Продифференцируем замену , отсюда . Подставляем:

.

2) . Подынтегральная функция является рациональной относительно . Здесь . Наименьшее общее кратное . Следовательно, нужно сделать подстановку :

Поделив числитель на знаменатель «уголком»

,

получаем:

.

3) . Сделаем замену: : . Произведем теперь замену: ; .

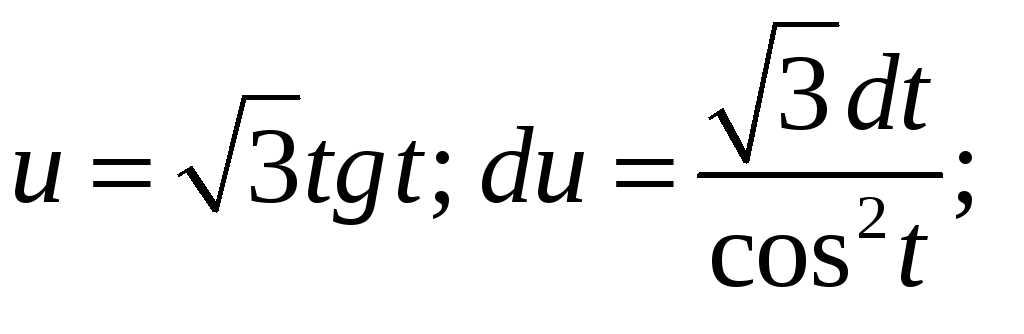
4) . Это интеграл от биномиального дифференциала. Здесь Поскольку - целое число, сделаем замену: . Таким образом, .

5) . Это интеграл от биномиального дифференциала. Здесь . Поскольку - целое число, сделаем замену: ; получим: . Интеграл

вычислим как интеграл от рациональной дроби. Разложим подынтегральное выражение на простейшие дроби, предварительно разложив на множители знаменатель:

. Имеем: , приведем правую часть к общему знаменателю и, отбросив его, получим:

. (21)

Полагая в (21) последовательно и , получим: , откуда . Приравнивая в (21) коэффициенты при , получаем: , подставив в последнее равенство найденные значения и , имеем: . Итак, получаем:

.

6) . Хотя интеграл не подпадает ни под один из п. 1-4, тем не менее, он сводится к сумме интегралов из п. 2:

. Имеем:

.

Аналогично вычисляется и второй интеграл. Просуммировав их, окончательно получим:

.