1. Неопределенный интеграл

   1. Понятие первообразной функции и неопределенного интеграла

Во многих вопросах науки и техники приходится по известной производной восстанавливать саму функцию. Например, используя ленту скоростемера, мы находим функцию скорости поезда в зависимости от времени. Но если мы хотим узнать, на каком километре пути находился поезд в тот или иной момент времени, нам нужно найти функцию зависимости пройденного пути от времени. Как известно, производной функции будет функция , поэтому наша задача свелась к нахождению по заданной функции неизвестной функции , для которой производной будет .

Определение. Функция в данном промежутке называется первообразной функцией для функции , если на всем промежутке функция является производной для функции , т.е. или, что то же самое, служит для дифференциалом, т.е. .

Теорема. Если в некотором (конечном или бесконечном) промежутке функция есть первообразная для , то и функция , где - любая постоянная, также будет первообразной. Обратно, каждая функция, первообразная для в промежутке , может быть представлена в этой форме.

В силу этой теоремы выражение , где - произвольная постоянная, представляет собой общий вид функции, которая имеет производную . Это выражение называется неопределенным интегралом и обозначается . Произведение называется подынтегральным выражением, а функция - подынтегральной функцией.

2. Таблица основных неопределенных интегралов.

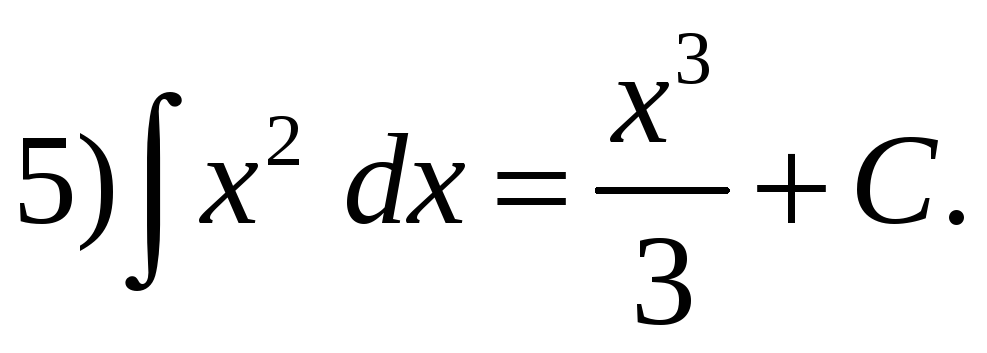
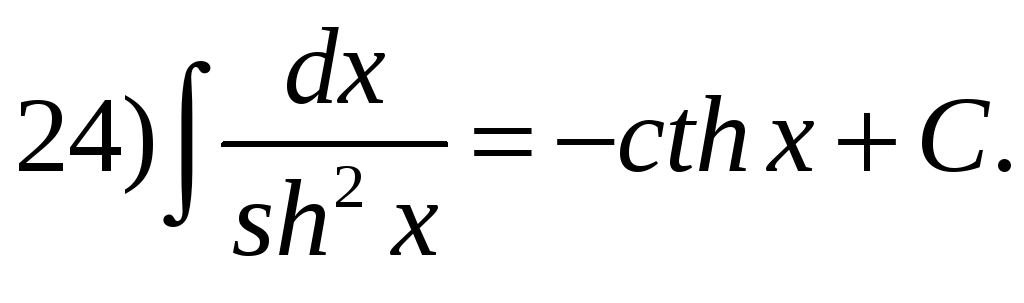
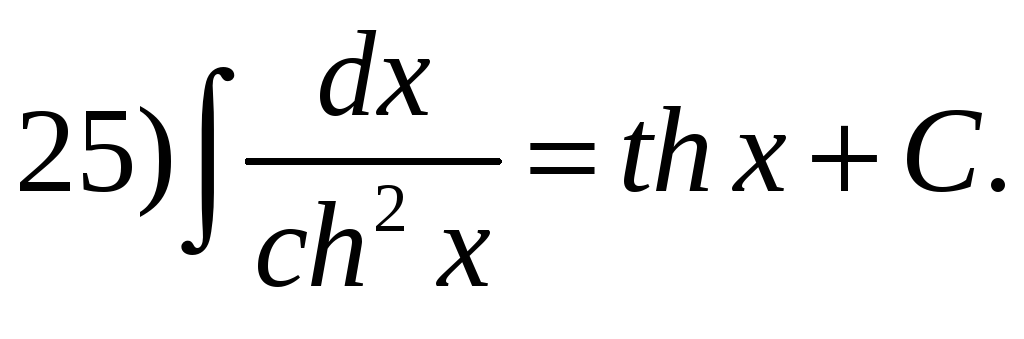
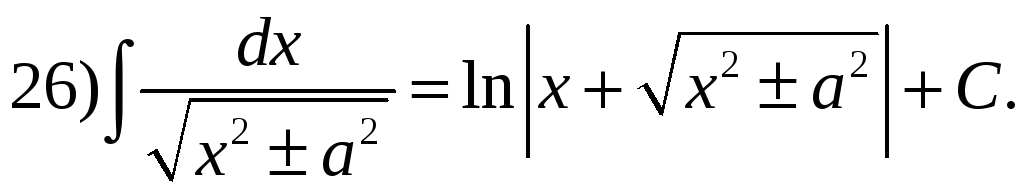
Дополнительно

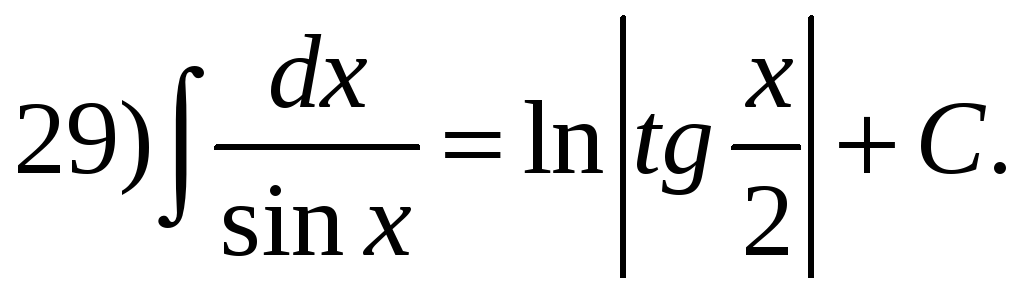
3. Простейшие правила интегрирования

1) Если - постоянная , то , т.е. постоянный множитель можно выносить из-под знака интеграла.

2) , т.е. неопределенный интеграл от суммы (разности) интегралов от каждой функции в отдельности.

Примеры

1)

2)

3)

4)

4. Интегрирование методом замены переменной

   1. Линейная замена

Если , то (1)

В самом деле, сделаем в интеграле замену , тогда по определению дифференциала откуда .

Итак,

Откуда и следует требуемое равенство.

Особенно часто встречаются случаи, когда или :

(2) (3)

Примеры

1)

2)

3) 4) 5)

6)

2. Замена с помощью подстановок

Замена переменной в неопределенном интеграле осуществляется с помощью подстановок двух видов:

1) где - новая переменная. В этом случае формула замены переменной имеет вид:

;

2) где - новая переменная. Формула замены при такой подстановке имеет вид:

Порядок замены переменной:

1. ввести новую переменную с помощью подстановки вида 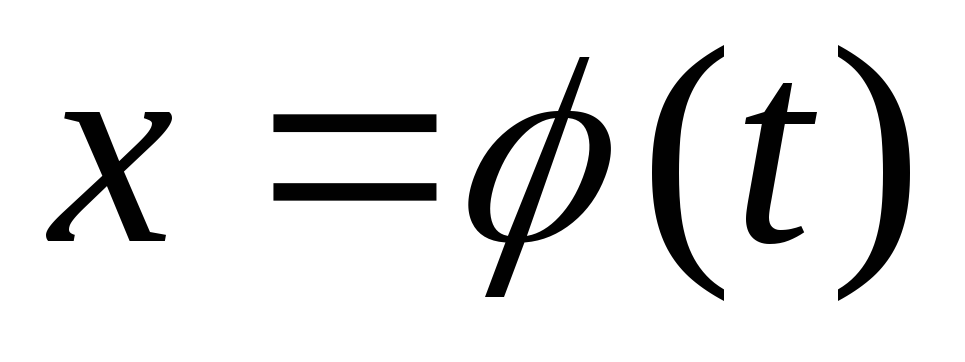или

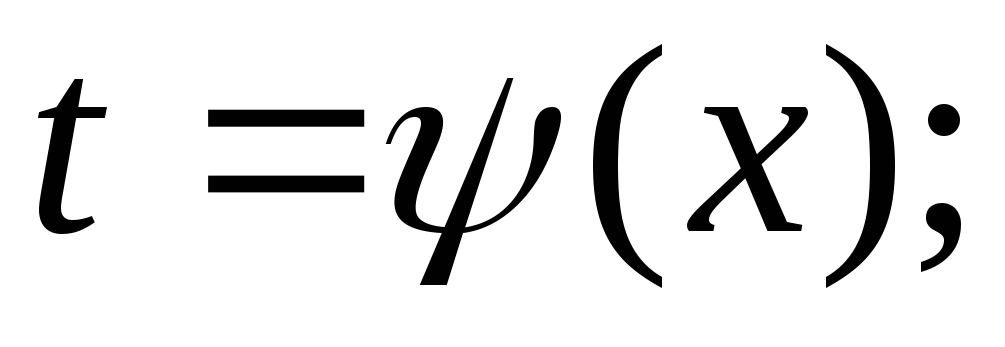
2. продифференцировать подстановку из п. 1: или ;

3. выразить все, что стоит под знаком интеграла, через новую переменную и вычислить полученный интеграл;

4. с помощью формулы из п.1 вернуться к старой переменной.

Наиболее часто встречаются подстановки, приведенные в табл. 1.

Таблица 1

Таблица основных замен

Выражение, встречающееся в интеграле	Рекомендуемая подстановка	Дифференциал
	или

Примеры

1) Сделаем замену переменной по формуле . Тогда . Выразив подынтегральное выражение через новую переменную, вычислим полученный интеграл:

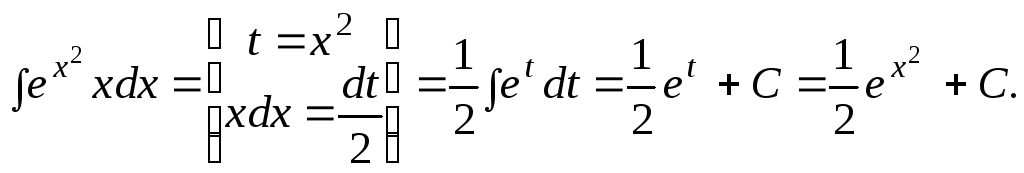
2)

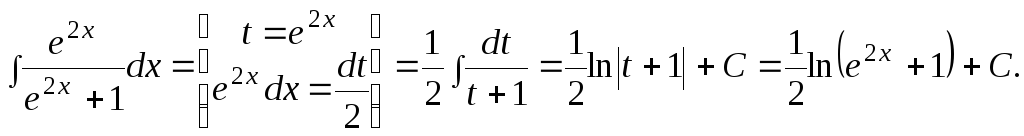
3)

4)

Найти подходящую замену – большое искусство. Иногда приходится делать последовательно две или несколько замен.

5)

В некоторых случаях из вида подынтегрального выражения ясно. Что удобнее сделать замену вида или , где - требуемая функция из второй колонки табл. 1; - постоянная. Если производите замену вида , будьте внимательны к знаку выражения .

6)

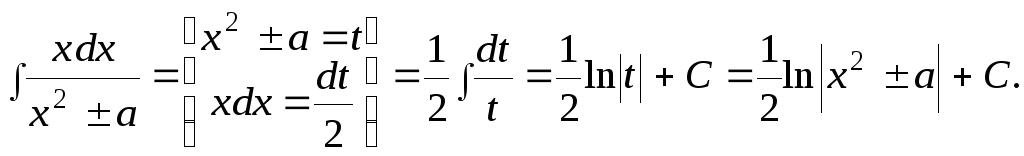
иногда соответствующее табл. 1 выражение приходится из подынтегрального выражения вычленять.

7) . Хотя выражения вида напрямую в интеграле нет, однако подстановка приводит к цели.

8) . Здесь также требуемое выражение приходится вычленять:

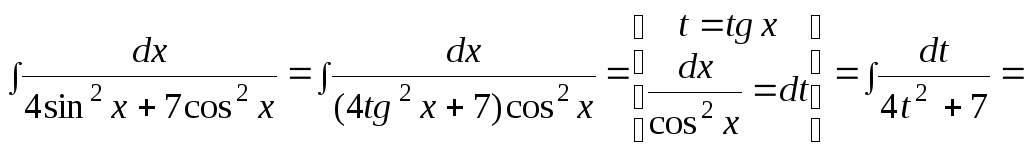
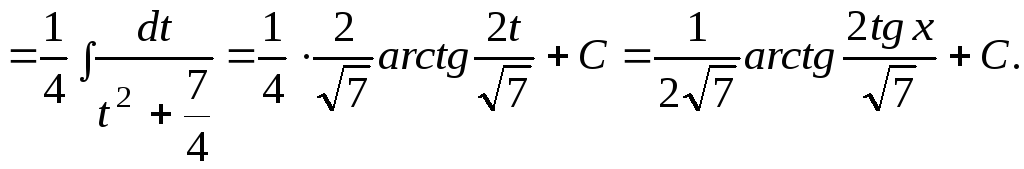
В зависимости от вида подынтегрального выражения, если в нем встречается соотношение вида , иногда удобно произвести замену или

.Тогда в первом случае, а во втором.

9)

В ряде случаев к цели приводит представление интеграла в виде суммы двух, один из которых табличный или приводится к нему линейной заменой, а второй требует замены переменной из табл. 1. Также возможен случай, когда оба интеграла требуют замены переменной, чаще всего, каждый – своей.

10) (4) Первый интеграл сводится к табличному линейной заменой:

Второй требует замены переменной по формуле :

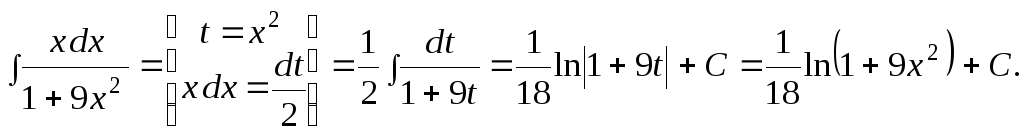
Подставив полученные результаты в (4), имеем: .

11) (5) Первый интеграл берется заменой :

второй – заменой :

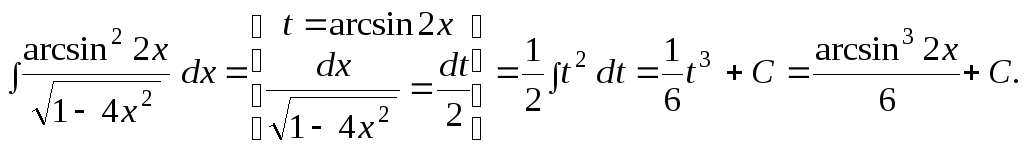
Подставив полученные результаты в (5), получаем окончательный ответ: