
- •1.1. Назначение, принцип действия и конструкция электроизмерительных приборов
- •1.2. Оценка показаний прибора
- •1.3. Шкала прибора
- •1.4. Класс точности прибора
- •1.5. Основные схемы включения приборов и их условные обозначения
- •1.6. Порядок проведения работы
- •1.7. Контрольные вопросы
- •2.1. Основные теоретические положения
- •2.2. Схема проведения испытаний
- •2.3. Порядок выполнения работы
- •2.4. Обработка результатов опыта
- •2.5. Контрольные вопросы
- •3.1. Основные теоретические положения
- •3.2. Схема проведения испытаний
- •3.3. Порядок выполнения работы
- •3.4. Обработка результатов опыта
- •3.5. Контрольные вопросы
- •1.1. Основные теоретические положения
- •1.2. Порядок выполнения работы
- •1.3. Обработка результатов опыта
- •1.4. Контрольные вопросы
- •4.1. Основные теоретические положения
- •4.2. Порядок выполнения работы
- •4.3. Обработка результатов опыта
- •4.4. Контрольные вопросы
2.5. Контрольные вопросы
1) Какая электрическая цепь называется сложной? Изобразите произвольную схему сложной электрической цепи, содержащую три источника ЭДС и несколько приемников.
2) Какие существуют методы для расчета сложных электрических цепей постоянного тока и где они применяются?
3) На чем основывается метод наложения, как производится расчет цепи по этому методу?
4) В цепи действует несколько источников питания. Некоторые из них работают в режиме генератора, а остальные – в режиме потребителя. По какому признаку определяется режим работы тех и других источников питания?
Лабораторная работа 3
ИССЛЕДОВАНИЕ ЦЕПИ ТРЕХФАЗНОГО ПЕРЕМЕННОГО ТОКА
ПРИ ВКЛЮЧЕНИИ АКТИВНЫХ НАГРУЗОК ЗВЕЗДОЙ И
ТРЕУГОЛЬНИКОМ
Цель работы: установить соотношения между линейными и фазными напряжениями и токами для нагрузок, включенных звездой, при различных режимах работы; выяснить назначение нулевого (нейтрального) провода в этих режимах; установить соотношения между напряжениями, линейными и фазными токами для нагрузок, включенных треугольником, при различных режимах работы; построить по опытным данным векторные диаграммы напряжений и токов трехфазной цепи; подсчитать мощность, потребляемую нагрузкой, при соединении звездой и треугольником 1, с. 111 – 118; 2, с. 125 – 137.
3.1. Основные теоретические положения
Трехфазная сеть, как правило, представлена симметричными, т. е. равными по абсолютному значению напряжениями со взаимным сдвигом по фазе на 120.
Для включения электроприемников (нагрузки) в сеть трехфазного тока их соединяют звездой или треугольником.
При включении нагрузки звездой (рис. 5) концы фаз, соединенные вместе, образуют нулевую точку, к которой может быть подключен провод, называемый нейтральным. В этом случае имеем четырехпроводную схему, в которой к потребителю подводятся линейные и фазные напряжения сети (если пренебречь сопротивлением соединительных проводов):
|
|
|
В общем случае
линейные напряжения
![]() ,
,![]() ,
,![]() связаны с фазными
связаны с фазными![]() ,
,![]() ,
,![]() следующими уравнениями:
следующими уравнениями:
|
|
П ри
соединении нагрузки звездой ток в
подводящих проводах будет одновременно
и током фазы:Iл
= Iф.
ри
соединении нагрузки звездой ток в
подводящих проводах будет одновременно
и током фазы:Iл
= Iф.
Если
сопротивления нагрузки отдельных
фаз равны между собой, т. е. za
=
zb
=
zc,
то такая нагрузка называется равномерной,
тогда для линейных и фазных напряжений
имеет место следующее соотношение:
![]() .
.
Векторная диаграмма напряжений и токов при равномерной активной нагрузке, соединенной звездой, представлена на рис 6, а
При равномерной нагрузке фаз сумма мгновенных значений тока всех фаз или геометрическая сумма векторов каждого тока равна нулю. Ток в нулевом проводе будет отсутствовать, следовательно, при равномерной нагрузке нет необходимости его подключать. Схема в этом случае становится трехпроводной.
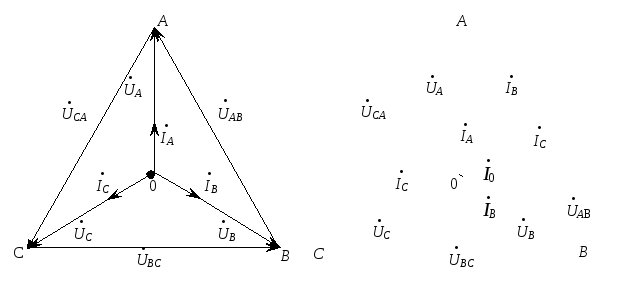
а б
Рис. 6. Векторные диаграммы напряжений и токов при равномерной (а) и
неравномерной (б) активной нагрузке фаз, соединенных звездой с
нулевым проводом
Неравномерная нагрузка, соединенная звездой, обычно подключается по четырехпроводной схеме, т. е. с нулевым проводом, так как при наличии нулевого провода, обладающего малым сопротивлением, неравномерная нагрузка не приводит к значительному изменению фазных напряжений.
Можно считать, что фазные напряжения при неравномерной нагрузке остаются такими же, как и для случая равномерной нагрузки:
![]() . (25)
. (25)
По нулевому проводу
будет протекать уравнительный ток I0,
при этом сумма всех токов
![]() .
.
Векторная диаграмма при неравномерной нагрузке фаз, соединенных звездой с нулевым проводом, представлена на рис. 6, б.
Отсутствие нулевого провода при неравномерной нагрузке нарушает нормальный режим работы установки. Фазные токи изменяются и устанавливаются так, чтобы их сумма была равна нулю. В результате этого происходит искажение симметрии фазных напряжений: фаза с меньшим сопротивлением оказывается по сравнению с нормальным под сниженным напряжением, а с большим сопротивлением – под повышенным.
Векторная диаграмма при отсутствии нулевого провода и неравномерной нагрузке представлена на рис. 7.
Мощность, потребляемая нагрузкой, для любого режима
![]() , (26)
, (26)
где
![]() ,
,![]() ,
,![]()
мощность фаз A,
B,
C.
мощность фаз A,
B,
C.
А ктивная
мощность каждой фазы
ктивная
мощность каждой фазы
![]() .
(27)
.
(27)
При включении
потребителей треугольником (рис. 8)
фазные нагрузки подключаются на линейные
напряжения, а поэтому фазные напряжения
равны линейным:
![]() .
Линейный ток каждой фазы равен разности
токов примыкающих фаз (геометрическая
разность векторов фазных токов):
.
Линейный ток каждой фазы равен разности
токов примыкающих фаз (геометрическая
разность векторов фазных токов):
![]() ; (28)
; (28)
![]() ; (29)
; (29)
![]() . (30)
. (30)
Векторная диаграмма напряжений и токов при равномерной активной нагрузке представлена на рис. 9. В этом случае линейные и фазные токи связаны между собой соотношением:

![]() .
(31)
.
(31)
При неравномерной нагрузке фаз соотношение (31) нарушается. Векторная диаграмма токов становится несимметричной (рис. 10), т. е. линейные провода загружаются неодинаково. Например, изменение нагрузки в одной из фаз влияет на изменение двух линейных токов и не влияет на величины фазных напряжений и токов двух других фаз, а также третьего линейного тока.
|
|
нагрузке |
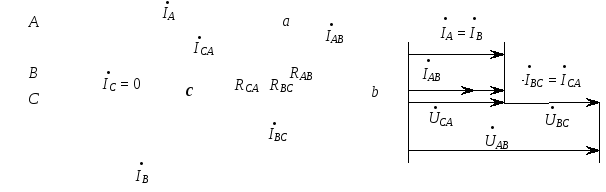
При
обрыве одного из линейных проводов,
например С
(рис. 11, а), нормальный режим работы
установки нарушается. Потребители фазы
А
будут находиться под нормальным фазным
напряжением Uф,
а потребители фаз В
и С
окажутся последовательно соединенными
и будут питаться от этого же напряжения.
В этом случае линейный ток
![]() равен току
равен току
![]() по первому закону Кирхгофа:
по первому закону Кирхгофа:
![]() ,
(32)
,
(32)
так как
![]() .
.
В данном режиме
работы трехфазной цепи соотношение
токов
![]() и
и![]() в обеих ветвях будет обратно пропорционально
сопротивлениям этих ветвей:
в обеих ветвях будет обратно пропорционально
сопротивлениям этих ветвей:
![]() ,
(33)
,
(33)
если
![]() ,
то фазный ток
,
то фазный ток![]() будет в два раза больше фазного тока
будет в два раза больше фазного тока![]() .
.
Фазное напряжение
![]() по-прежнему
будет равно линейному
по-прежнему
будет равно линейному
![]() ,
а фазные напряжения
,
а фазные напряжения![]() и
и
![]() будут
равны между собой и равны половине
линейного
будут
равны между собой и равны половине
линейного
![]() (при
(при
![]() =
=
![]() )
(рис. 11, б).
)
(рис. 11, б).
Мощность, потребляемая симметричной нагрузкой при соединении звездой и треугольником, определяется по одним и тем же формулам:
![]() (34)
(34)
или
![]() .(35)
.(35)
а б
Рис. 11. Схема (а) и векторная диаграмма напряжений и токов (б) при обрыве
линейного провода

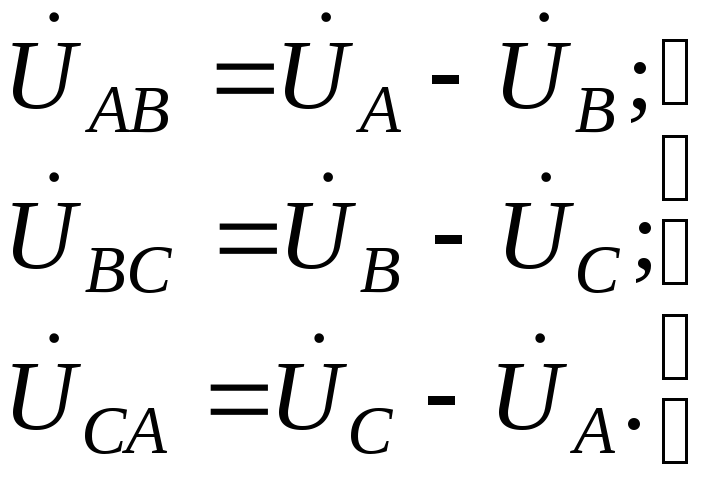 (24)
(24) Рис.
9. Векторная диаграмма напряжений и
токов при равномерной нагрузке
Рис.
9. Векторная диаграмма напряжений и
токов при равномерной нагрузке Рис. 10. Векторная
диаграмма напряжений и токов при
неравномерной
Рис. 10. Векторная
диаграмма напряжений и токов при
неравномерной