3. Анализ и синтез комбинационных устройств

3.1. Анализ комбинационных дискретных устройств

Задача анализа комбинационного дискретного устройства состоит в нахождении ФАЛ, реализованной устройством. Функция алгебры логики может быть представлена в аналитическом виде или в форме таблицы истинности. Анализ проводят для определения функциональных свойств комбинационного устройства по его схеме или для проверки правильности функционирования разработанной схемы. Такая проверка необходима, так как при разработке сложных устройств не всегда удается достаточно полно формализовать предъявляемые к схеме требования, которые в этом случае учитываются на основании эвристических соображений разработчика. Анализ может проводиться также с целью определения работоспособности схемы в режимах, отличающихся от заданных при проектировании.

Работу устройства железнодорожной автоматики необходимо анализировать при повреждении некоторых его элементов. При этом важно выполнить основное требование: любое повреждение не должно приводить к изменению алгоритма функционирования, которое может нарушить условия обеспечения безопасности движения поездов. При анализе ставят задачу определения возможности упрощения схемы устройства. Это достигается соответствующим преобразованием и минимизацией ФАЛ. Особой задачей анализа является выяснение поведения дискретного устройства в переходных режимах и. выявление возможностей нарушений работы в эти периоды.

Анализ реальных схем с точки зрения логики их работы проводят в два этапа. Сначала из имеющейся принципиальной схемы удаляют все несущественные, вспомогательные элементы, которые не влияют на логику работы схемы, а лишь обеспечивают устойчивость ее работы. Получается схема, состоящая из элементов, выполняющих только логические функции. Затем анализируют полученную схему.

Метод нахождения ФАЛ определяется прежде всего схемой. При контактных элементах ФАЛ записывают непосредственно по схеме. Для схемы, приведенной на рис. 3.1, а, функция алгебры логики

.

Рис. 3.1

По данному выражению может быть составлена таблица истинности в форме карты Карно (рис. 3.1, б). Из этого следует, что схема может быть упрощена (рис. 3.1, в) и МДНФ запишется так:

.

Анализ схем на бесконтактных логических элементах сводится к получению формул последовательной подстановкой. Для анализа схемы (рис. 3.2) введем промежуточные переменные:

; ; ;

;

.

Рис. 3.2

Полученные выражения позволяют определить значение функции алгебры логики.

3.2. Синтез комбинационных дискретных устройств

Синтез комбинационного ДУ состоит в построении принципиальной схемы по заданному словесному описанию алгоритма работы. Синтез проводят в несколько этапов. Сначала вводят входные переменные и выходные функции. Затем с использованием таблицы истинности задают БФ, отображающие соотношение между состояниями входов и выходов в каждый данный момент времени. В дальнейшем БФ представляют в базисе И, ИЛИ, НЕ и находят их минимальные формы. На заключительных этапах синтеза выбирают элементный базис и строят принципиальную схему ДУ.

Алгоритм 3.1. Синтез комбинационного дискретного устройства. 1. Обозначение входных переменных и выходных функций, отображающих состояния входов и выходов дискретного устройства. 2. Задание ФАЛ с использованием таблиц истинности. 3. Запись ФАЛ в базисе И, ИЛИ, НЕ. 4. Получение минимальных форм ФАЛ в базисе И, ИЛИ, НЕ. 5. Выбор элементного базиса. 6. Запись ФАЛ в выбранном базисе. 7. Построение принципиальной схемы.

Рассмотрим следующий пример.

Синтезировать ДУ, управляющее двигателем насоса для доливки воды в резервуар (рис. 3.3). Двигатель насоса должен включаться автоматически при уровне воды в резервуаре ниже минимального, а также при нажатии кнопки ручного управления КРУ, если верхний уровень воды не достигнут. В случае превышения нижнего и верхнего уровней размыкаются контакты соответственно датчиков Д1 и Д2. Исполнительным элементом является пускатель двигателя ПД. Вопросы удержания двигателя во включенном состоянии и его остановки не рассматриваются.

Рис. 3.3

Введем входные переменные:

В соответствии со словесным описанием алгоритма работы ДУ и принятыми выходной функцией и входными переменными заполняем таблицу истинности (табл. 3.1).

Таблица 3.1

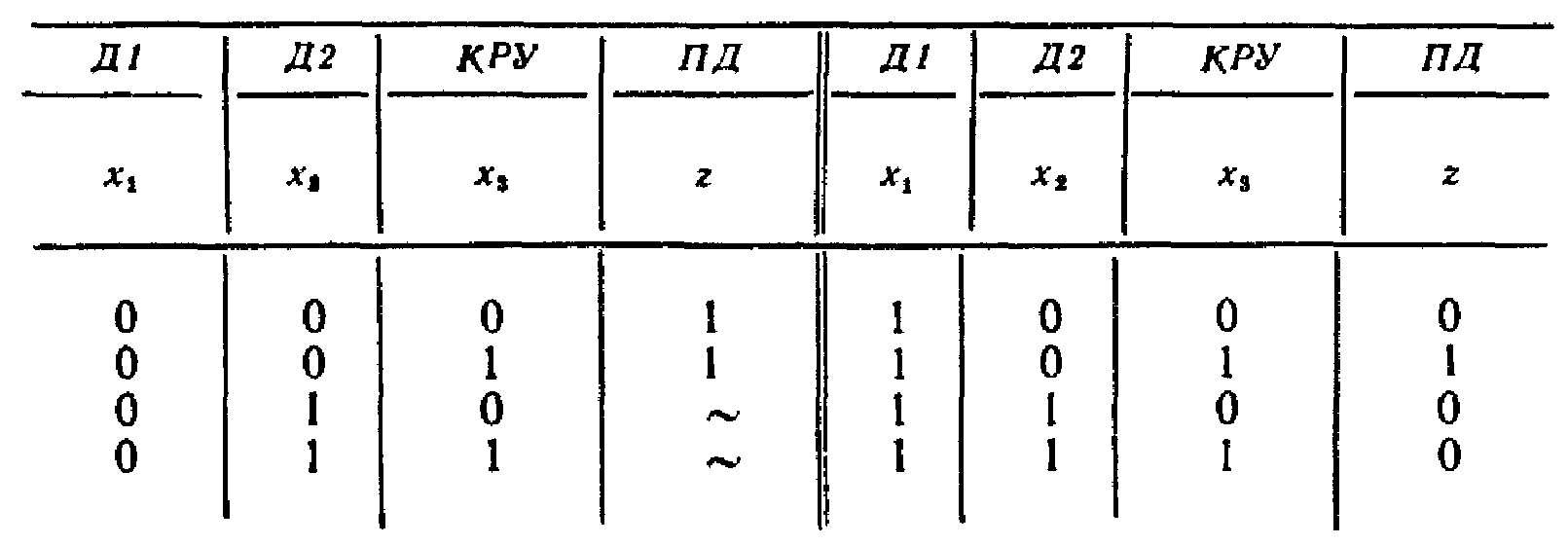
В третьей и четвертой строках таблицы значения выходной функции не определены (поставлен знак ~), так как соответствующие комбинации входных переменных х₁ и х₂ отражают состояния, которые не могут иметь место в процессе работы дискретного устройства: верхний уровень достигнут, а нижний нет.

Д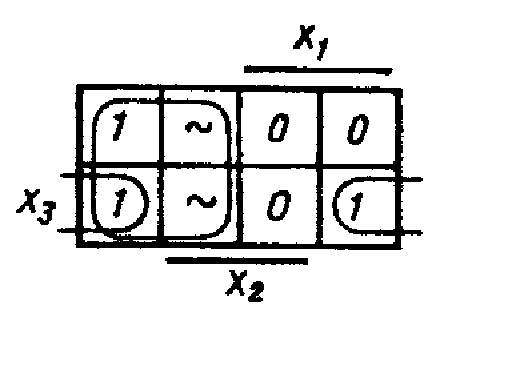ля нахождения МДНФ используем карту Карно. При неиспользуемых наборах значение БФ целесообразно принять равным единице, тогда

Для реализации БФ используем контакты датчиков Д1, Д2 и кнопки КРУ (рис. 3.4).

Рис. 3.4

Построение комбинационных схем на электромагнитных реле, на базе диодной матрицы, на логических элементах в базисах (И, ИЛИ, НЕ), (И-НЕ), (ИЛИ-НЕ) подробно рассмотрено в методических указаниях к курсовому проектированию и методических указаниях к выполнению лабораторных работ по дисциплине «Теория дискретных устройств железнодорожной автоматики и телемеханики».

Применение элементов И-ИЛИ-НЕ подробно рассмотрено в методических указаниях к курсовому проектированию.