
вариант №9
.docxЗадания для экзаменующегося по математике за 1 курс
Часть А. Решите задание и выберите правильный ответ:
А
1. Вычислите:
(3*4)-2 +
(3-1)-2
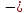 (144)-1
+ (3-2)0
(144)-1
+ (3-2)0
1) 12 2) 14 3) 144 4) 10
А 2. По графику функции, изображенному на рисунке, укажите множество значений функции
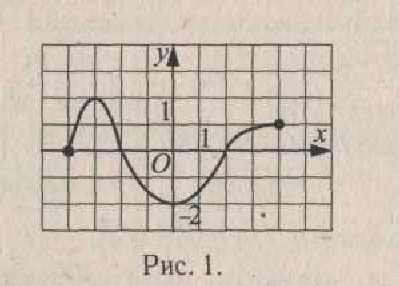
1) [–2; 2] 2) (–2; 2) 3) (–4; 4) 4) [–4; 4]
А 3. Найдите справедливое равенство:
-
arcsin
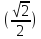 =
=
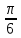 ; 2)
arcsin(
; 2)
arcsin(

 =
=
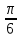 ;
3)
arcsin
;
3)
arcsin
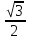 =
=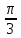 ;
4)
arcsin1=
;
4)
arcsin1=
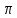
А
4.
Решите уравнение:
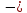 sin
sin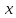 =
=
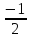
1)
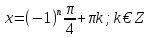 2)
2)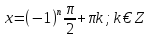
3)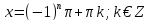 4)
4)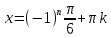 ,
k€Z
,
k€Z
А
5 .
Найдите cos
2t
, если
известно, что
cos
.
Найдите cos
2t
, если
известно, что
cos
 =
=
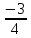 ,
,
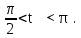
1)
−
 2)
2)
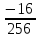 3)
3)
 4)
4)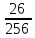
А
6 .
Упростите
выражение:
.
Упростите
выражение:
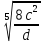 :
:
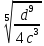
1)4cd
2) cd
3) 2cd2
4) 2c5d5
cd
3) 2cd2
4) 2c5d5
А
7 . Найдите
все целые решения неравенства: (
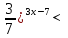 (
(
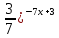
1) (- ∞; 1) 2) ( 1 ; ∞) 3) (2 ; ∞) 4) (- 4; ∞)
А
8 . Вычислить:
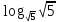 +
+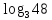 - log316
- log316
1)
 2) 3 3)
16
4) 2
2) 3 3)
16
4) 2
А 9 . Образующая конуса равна 7,5см, высота 6см. Найти объём конуса.
-
200 π с
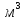 2) 40,5 π
с
2) 40,5 π
с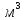 3) 120,5
π с
3) 120,5
π с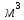 4)
20,25
π с
4)
20,25
π с
А 10 . Если сфера проходит через все вершины куба с длиной ребра 11, то радиус сферы равен:
1)
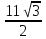 2)
2)
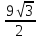 3)
3)
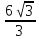 4)
4)
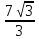
А 11. Точка А находится от плоскости на расстоянии 32 см и из нее проведена наклонная, равная 68см. Чему равна проекция.
1) 80 2) 60 3) 100 4) 120
А
12 . Упростите
выражение:
 + tgα*ctgα
+ tgα*ctgα
1) 1+tg2α 2) sinα 3) 1+ tgα 4) 1+ ctg2α
Часть В. Решите задание и запишите правильный ответ
В 1 . Найдите наибольшее и наименьшее значения функции
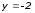
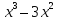 +
4 = 0 на отрезке
+
4 = 0 на отрезке
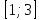
В 2 . Сколько килограмм краски потребуется для ремонта кабинета, если его длина 4м, ширина 6м, высота 2м. Расход краски 400 г на 1 м2
В
3 . Решите
иррациональное уравнение: 8 x=
x=

В 4. Найдите вероятность того, что при однократном бросании игральной кости выпадет четное число очков.
Часть С. Представьте развёрнутое решение
С 1 . Основание пирамиды равнобедренный треугольник со сторонами 120см, 68см, и 68см. Её высота проходит через вершину угла , противолежащего большей стороне и равна 36 см. Найдите боковую поверхность пирамиды.
С
2 . Для функции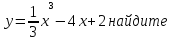 координаты точки её графика, в которых
касательные к нему параллельны оси
абсцисс.
координаты точки её графика, в которых
касательные к нему параллельны оси
абсцисс.
С 3 . Вычислите площадь фигуры, ограниченной осями координат, графиком функции
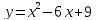 и прямой х = 2.
и прямой х = 2.
