25 Эдс катушечных групп и фазы.

Катушечная группа состоит из qодинаковых катушек (секций), расположенных в соседних пазах (рисунок 12).

Рисунок 12 – Катушечная группа

ЭДС в катушках сдвинуты по фазе на угол α_эл. Все секции катушечной группы сдвинуты последовательно. Суммарная ЭДС равна геометрической сумме отдельных (рисунок 13).

Рисунок 13 – Секции катушечной группы

Эта сумма меньше арифметической суммы Е­_q1<qE_k1. Отношение– коэффициент распределения обмотки. Его величину можно определить с помощью векторной диаграммы. Рассматривая векторы Е_Ккак часть многоугольника, вписанного в окружность радиусаR, получим

.

Суммарная ЭДС катушечной группы равна

.

Двухслойная обмотка фазы состоит из 2р катушечных групп, а однослойная – из р групп. Катушечные группы могут быть соединены последовательно, параллельно или последовательно-параллельно. Все катушечные группы состоят из qкатушек с числом витковw_k. Если обмотка фазы состоит из а параллельных ветвей, то общее число последовательно соединенных витков фазы, определяющее ее ЭДС равно:

– для двухслойной обмотки

;

– для однослойной обмотки

.

Тогда ЭДС фазы обмотки от поля первой гармоники равно

.

26 Улучшение формы кривой эдс.

В обмотке фазы кроме ЭДС первой гармоники индуцируется ЭДС от высших гармоник магнитного поля. ЭДС то высших гармоник определяется по формуле

, (13)

где f_ν=ν∙f₁– частота ν-ой гармоники;

Ф_ν– магнитный поток ν-ой гармоники;

К_νy, К_рν– соответственно коэффициенты укорочения и распределения для ν-ой гармоники.

Число полюсов для ν-ой гармоники в ν раз больше, чем для первой. Поэтому электрические углы сдвига фаз между ЭДС для высших гармоник будут в ν раз больше, чем для первой. С учетом этого имеем

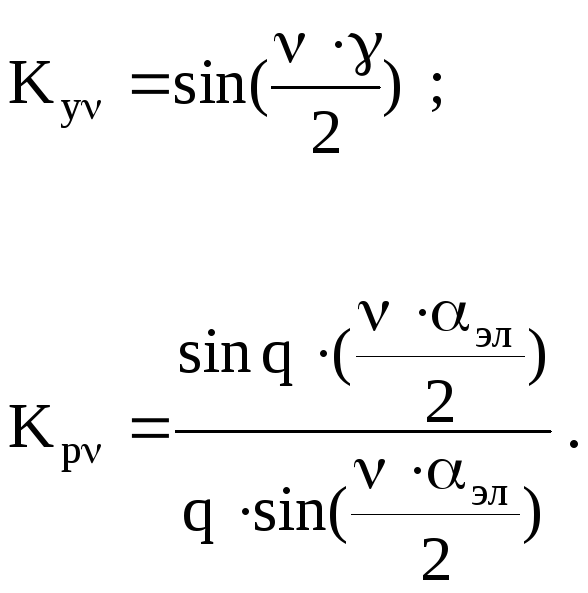
Результирующая ЭДС (действующее значение) фазы равно

.

Укорочение шага обмотки и распределение ее по пазам приводит к уменьшению ЭДС высших гармоник. При укорочении шага обмотки происходит более резкое уменьшение ЭДС высших гармоник. При укорочении шага на 1/ν часть полюсного деления в кривой ЭДС полностью исчезает ν-ая гармоника. При у=τ_nЭДС пятой гармоники в проводниках обмотки под противоположными полюсами суммируются (рисунок 14). При у=ЭДС пятой гармоники в проводниках обмотки вычитаются. Поэтому пятая гармоника будет отсутствовать. При этом также уменьшаются ЭДС других гармоник.

Рисунок 14 – ЭДС пятой гармоники

При выборе шага обмотки стремятся, чтобы были полностью исключены и значительно ослаблены ЭДС наиболее сильно проявляемых гармоник. Это третья, пятая и седьмая гармоники. Третью гармонику в линейной ЭДС обычно уничтожают соединением трехфазной обмотки в звезду. Для ослабления пятой и седьмой гармоник шаг обмотки выбирают в пределах от до. ПриПри

При увеличении числа пазов на qна полс и фазу сильно уменьшается коэффициенты распределения К_ρν. Это объясняется тем, что ЭДС катушек катушечных групп для ν-ых гармоник будут сдвинуты относительно друг друга на угол, в ν раз больший, чем для первой гармоники, вследствие чего их геометрическая сумма уменьшается.

Кривая результирующей ЭДС обмотки с большим qближе к синусоиде. Однако при этом машина становится дороже. Обычноq=2…6.

Пульсации магнитного поля возникают вследствие зубчатого строения статора и ротора. Эти гармоники называются зубчатыми. Их порядок зависит от числа зубцов (рисунок 15).

Рисунок 15 – Зубчатое строение статора

Для уменьшения зубцовых гармоник в кривой ЭДС изменяют скос пазов или скос полюсов. Если скос выполняется на статоре, то он производится на одно зубцовое деление ротора, а если на роторе, то на одно зубцовое деление статора. При скосе пазов можно полностью уничтожить зубцовые гармоники. Физически это можно объяснить тем, что у зубцевых гармоник магнитное поле под зубцом и пазом имеет противоположную полярность. Вследствие этого в отдельных участках проводника, расположенного в скошенном пазу противоположного магнитного провода, индуцируются одинаковые по величине, но противоположно направленные ЭДС. Их сумма равна нулю (рисунок 16).

Рисунок 16 – Скос пазов

При скосе пазов уменьшается ЭДС первой гармоники. Это учитывается коэффициентом скоса К_ск. Для определения К_скзаменим проводник в скошенном пазу некоторым числом прямых проводников очень малой длины. Геометрическая сумма ЭДС этих малых проводников будет равна хорде окружности радиусаR, на которую опираются стороны угла γ_с(рисунок 17)

Рисунок 17 – определение К_ск

Коэффициент скоса К_скравен отношению геометрической сумме ЭДС к арифметической

.

Для ν-ой гармоники

.

В общем случае ЭДС фазы определяется по формулам:

для общей гармоники

(14)

для ν-ой гармоники

(15)

где – обмоточные коэффициенты.