
- •Проектирование кривошипно - ползунного механизма
- •Самарская государственная академия путей сообщения, 2004
- •1. Кинематический синтез механизма
- •Рассмотрим методику синтеза механизмов по этим параметрам.
- •1.2. Синтез центрального механизма по ходу ползуна и
- •Скорость точки в
- •2. Кинематический и кинетостатический анализ кривошипно-ползунного механизма
- •2.1. Кинематический и кинетостатический анализ
- •2.1.1. Определение траекторий движения точек звеньев механизма
- •2.1.3. Кинетостатический анализ механизма
- •2.1.4. Определение уравновешивающего момента
- •2.2. Алгоритм кинематического и кинетостатического анализа с использованием эвм
2. Кинематический и кинетостатический анализ кривошипно-ползунного механизма
Построив по рассчитанным размерам план механизма, студент приступает к его кинематическому и кинетостатическому анализу. Как указывалось выше, для заданного (0) положения входного звена анализ производится графо- аналитическим методом, для остальных (n-1) положений входного звена – аналитическим методом с помощью ЭВМ.
2.1. Кинематический и кинетостатический анализ
графо- аналитическим методом
Методику выполнения кинематического и кинетостатического анализа рассмотрим на примере механизма, приведенного в приложении.
2.1.1. Определение траекторий движения точек звеньев механизма
Поскольку кривошип АВ совершает
вращательное движение, то траекторией
движения точки В является окружность.
Разделим окружность на 8-12 равных частей
(точки В1,
В2
и т.д. В12)
и построим соответствующие положения
кривошипа. Из каждой точки Вi
раствором циркуля, равным длине шатуна
(в выбранном масштабе), делаем засечки
на направляющей ползуна, т.е. определяем
положения шатуна (точки С), соответствующие
i-
му положению кривошипа. Для определения
крайних положений ползуна на его
направляющей делаем засечки из точки
А радиусами, равными сумме (![]() +r=АС)
и разности
+r=АС)
и разности
![]() )
длин шатуна и кривошипа. Расстояние
между полученными точками должно быть
равно (в принятом масштабе
)
длин шатуна и кривошипа. Расстояние
между полученными точками должно быть
равно (в принятом масштабе![]() )
заданному ходу ползунаSn.
Строим положения кривошипа, соответствующие
крайним положениям ползуна и замеряем
углы между этими положениями. Больший
угол обозначаем р
( угол поворота кривошипа за рабочий
ход ползуна), а меньший - х
( угол поворота кривошипа за холостой
ход ползуна).
)
заданному ходу ползунаSn.
Строим положения кривошипа, соответствующие
крайним положениям ползуна и замеряем
углы между этими положениями. Больший
угол обозначаем р
( угол поворота кривошипа за рабочий
ход ползуна), а меньший - х
( угол поворота кривошипа за холостой
ход ползуна).![]()
Соединяя одноименные точки Вi и Сi получаем различные положения шатуна. Находим положение центра масс шатуна (S2i) на каждом положении шатуна. Соединив плавной кривой точки S2i, получаем траекторию движения центра масс шатуна (шатунную кривую).
2.1.2. Определение скоростей и ускорений движения точек и звеньев механизма
Как известно, кинематический анализ выполняется в последовательности, предусмотренной формулой строения механизма, поэтому начинаем кинематический анализ с основного двухзвенного механизма, состоящего из кривошипа (1) и стойки (4).
Определяем скорость точки В. Поскольку точка В вращается вокруг неподвижной точки А с постоянной угловой скоростью 1, то
VB =1r ; VB= 12 c-1 0,0192 м =0,2304 м/с.
Вектор
![]() АВ
и направлен в направлении угловой
скорости1.
АВ
и направлен в направлении угловой
скорости1.
В соответствии с формулой строения механизма переходим к структурной группе шатун- ползун (группа Ассура 2-3).
Для определения скорости точки С рассмотрим ее движение со звеном 2 (шатун) и звеном 3 (ползун). Шатун совершает плоское движение, которое состоит из поступательного (переносного) движения вместе с точкой, параметры движения которой известны (точка В), и вращательного ( относительного) движения вокруг этой точки. Следовательно,
![]() ,
,
где
![]() - линейная скорость точки С во вращательном
движении относительно точки В (направлена
перпендикулярно ВС).
- линейная скорость точки С во вращательном
движении относительно точки В (направлена
перпендикулярно ВС).
Рассматривая движение точки С со звеном 3, запишем
![]() ,
,
где ![]() - скорость точки, принадлежащей
направляющей (
- скорость точки, принадлежащей
направляющей (![]() = 0);
= 0);
![]() -
скорость движения ползуна по направляющей
(
-
скорость движения ползуна по направляющей
(![]() параллельна
направляющей).
параллельна
направляющей).
Полученные уравнения решаются графически путем построения плана скоростей.
Через точку р, выбранную в качестве полюса плана скоростей, проводим линию, перпендикулярную АВ, и откладываем вектор скорости точки В. Определяем масштаб плана скоростей:
КV
 ,
,
где
![]() -
длина вектора, изображающего на плане
скоростей вектор скорости точки В;
-
длина вектора, изображающего на плане
скоростей вектор скорости точки В;
КV=![]()
![]() .
.
Через точку в проводим линию, перпендикулярную ВС (линию, по которой направлен вектор скорости относительного вращательного движения). Через полюс (точка р) проводим линию, параллельную направляющей. Пересечение этих линий определяет положение точки с на плане скоростей. По правилу сложения векторов определяем направления найденных скоростей (оба вектора направлены к точке с). Измерив длины полученных векторов, получим:
вс КV =VСВ ; VСВ=85 мм 0,0025м/с мм=0,212 м/с ;
рс КV =VС ; VС=84 мм 0,0025м/с мм=0,21м/с .
Определяем мгновенное значение угловой скорости шатуна:
 ;
;
![]() с-1.
с-1.
Для
определения направления угловой скорости
звена 2 мысленно переносим вектор
линейной скорости точки С
в относительном вращательном движении
(вектор
![]() )
с плана скоростей в точкуС
плана механизма. Угловая скорость шатуна
направлена по часовой стрелке. Показываем
направление 2
на плане
механизма.
)
с плана скоростей в точкуС
плана механизма. Угловая скорость шатуна
направлена по часовой стрелке. Показываем
направление 2
на плане
механизма.
Определяем ускорение точки В. Так как кривошип вращается с постоянной угловой скоростью 1 , то
![]() ;
;![]()
![]() (12 с-1)2
0,0192 м = 2,76 м/с2.
(12 с-1)2
0,0192 м = 2,76 м/с2.
Вектор
![]() направлен по радиусу (по кривошипу) к
центру вращения, т.е. к точке А.
направлен по радиусу (по кривошипу) к
центру вращения, т.е. к точке А.
Для определения абсолютного ускорения точки С запишем уравнения:
![]() ;
(2.1)
;
(2.1)
![]() ,
(2.2)
,
(2.2)
где ![]() -
полное относительное ускорение точки
С в ее вращательном движении относительно
точки В;
-
полное относительное ускорение точки
С в ее вращательном движении относительно
точки В;
![]() ,
,![]() - нормальное и тангенциальное ускорение
точки С в ее относительном вращательном
движении относительно точки В;
- нормальное и тангенциальное ускорение
точки С в ее относительном вращательном
движении относительно точки В;
![]() -
ускорение точкиD,
принадлежащей направляющей;
-
ускорение точкиD,
принадлежащей направляющей;
![]() -
ускорение точки С относительно
направляющей.
-
ускорение точки С относительно
направляющей.
![]() ;
;
![]() .
.
Вектор
![]() направлен
вдоль звена ВС к точке В.
направлен
вдоль звена ВС к точке В.
Вектор
![]() направлен по линии, перпендикулярной
ВС.
направлен по линии, перпендикулярной
ВС.
Вектор
![]() направлен
по линии, параллельной направляющей.
направлен
по линии, параллельной направляющей.
Полученную систему векторных уравнений решаем графически путем построения плана ускорений.
Через произвольную точку , принятую за полюс плана ускорений, проводим линию, параллельную АВ, и на ней откладываем вектор, изображающий ускорение точки В. Определяем масштаб плана ускорений:
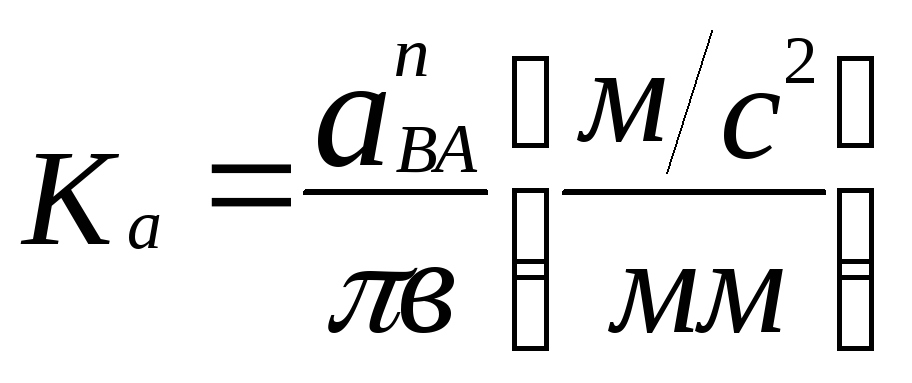 ;
;
![]() .
.
Т.к.
уравнение (2.1) представляет собой
векторную сумму, то через точку в
проводим линию, параллельную звену ВС,
и на ней в выбранном масштабе откладываем
отрезок вс,
изображающий на плане ускорений вектор
нормального ускорения точки С
при ее вращении относительно точки В
(![]() )
.
)
.
 ;
;
![]() .
.
Через точку с проводим линию, перпендикулярную звену ВС (линию, по которой направлен вектор тангенциального ускорения точки С в ее относительном вращательном движении).
Согласно уравнению (2.2) через полюс проводим линию, параллельную направляющей. Пересечение линий, перпендикулярной ВС и параллельной направляющей, определяет положение т. с на плане ускорений. Вектор сс, изображающий тангенциальное ускорение т. с, направлен
от с к с.
![]() ;
;
![]() .
.
Вектор с, изображающий абсолютное ускорение точки С, направлен от полюса к точке с.
с
Kа=ас
;
![]() .
.
Соединив на плане ускорений точки в и с найдем вектор, изображающий вектор полного относительного ускорения точки C относительно точки В. Он направлен от точки в к точке c :
![]() ;
;
![]() .
.
Определяем мгновенное значение углового ускорения шатуна:
 ;
;
![]() .
.
Методика определения направления углового ускорения аналогична методике определения угловой скорости. В рассматриваемом примере угловое ускорение шатуна направлено против часовой стрелки. Для определения ускорений центров масс звеньев воспользуемся свойством подобия планов ускорений. Ускорение центра масс кривошипа:
 .
.
Ускорение центра масс ползуна
![]() .
.
Для
нахождения ускорения центра масс шатуна
нанесем точку S2
на линию вс
плана ускорений и соединим ее с полюсом
().
Вектор
![]() изображает на плане ускорений вектор
абсолютного ускорения центра масс
шатуна.
изображает на плане ускорений вектор
абсолютного ускорения центра масс
шатуна.
![]() .
.
В соответствии с первым свойством планов ускорений этот вектор направлен от полюса.
