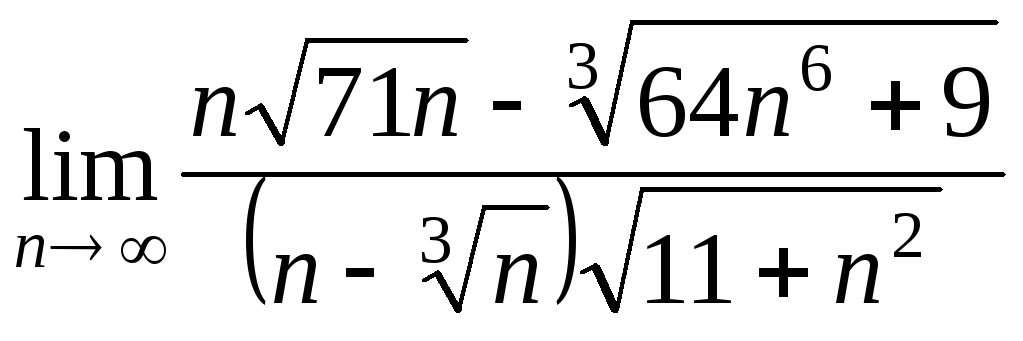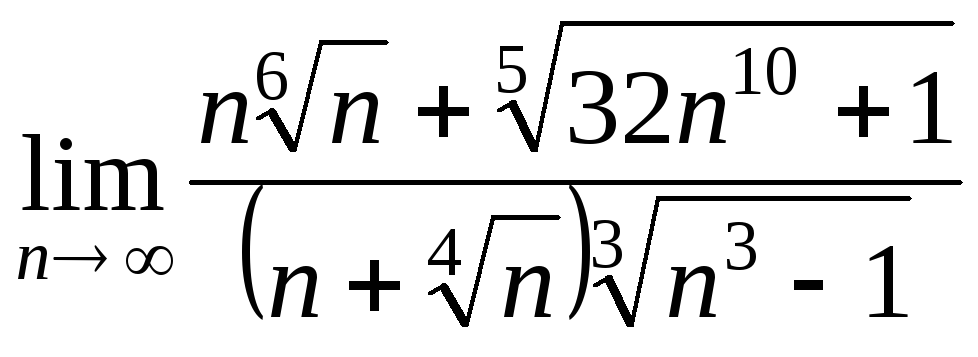Решение типового варианта
Задание
1. Найти
области определения и значений функции
.
Решение.
Логарифмическая функция определена,
если
,
,
что возможно при
.
Область
D
определения функции
Так
как в D
,
то интервал
- область значений функцииЕ.
Задание 2. Исследовать функцию на четность или нечетность
а)
.
Решение. Подставим в функцию вместо х значение –х:
Так
как выполняется равенство
,
то данная функция является четной.
б)
.
Решение.
Так
как выполняется равенство
,
то данная функция является нечетной.
в)
Исследовать функцию на четность и
нечетность
.
Решение.
,
т.е. данная функция ни четная, ни нечетная,
это функция общего вида.
Задание
3.
Найти наименьший период функции
.
Решение.
Период для функций
и
равен
.
Функция
имеет период в 3 раза меньше, т.е.
,
.
Наименьший период суммы
должен быть таким, чтобы
и
помещались в нем целое число раз. В
данном случае
.
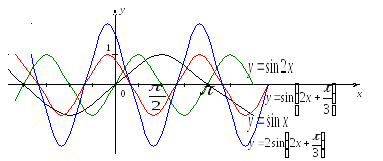
Задание 4. Построить график функции
а)
.
Решение.
Строим график
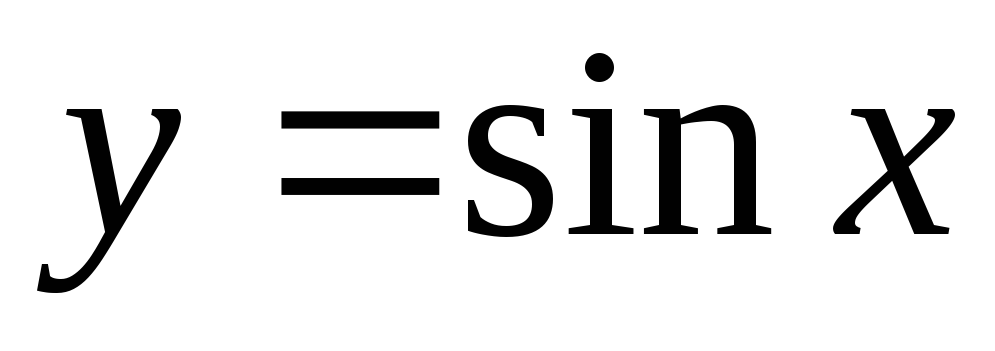;сжимаем его вдоль оси
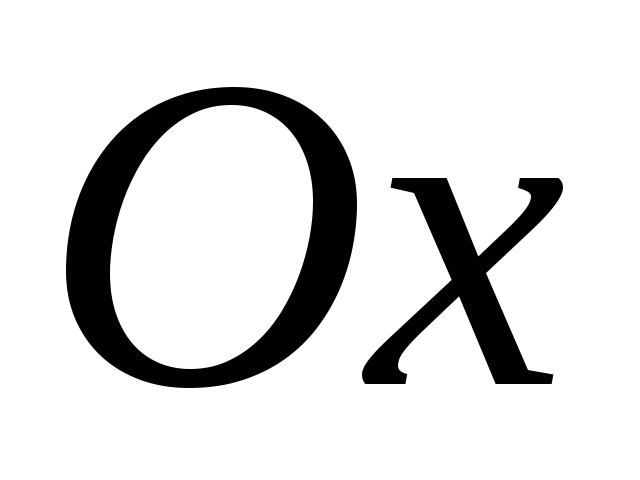в
2 раза, получаем график
;сдвигаем график
влево на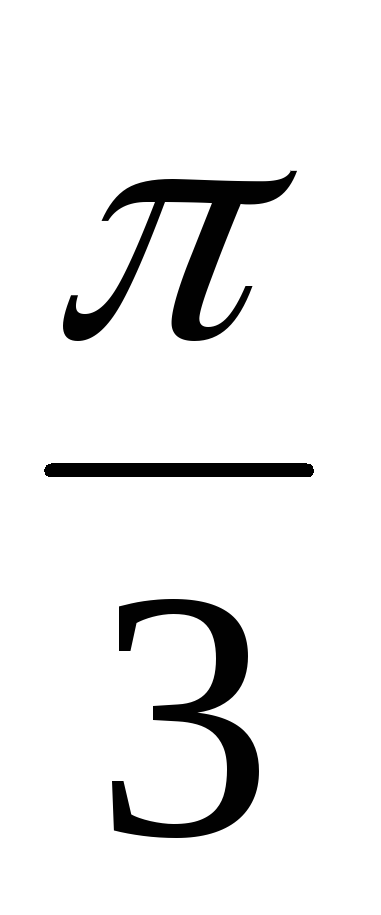
и получаем график
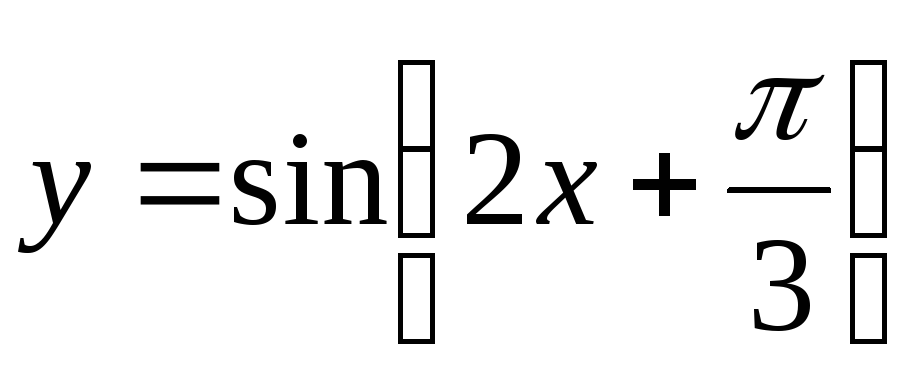;растягиваем график
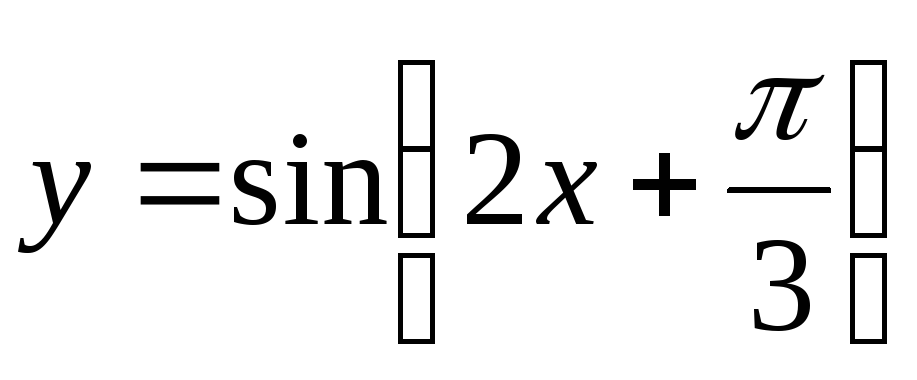вдоль оси
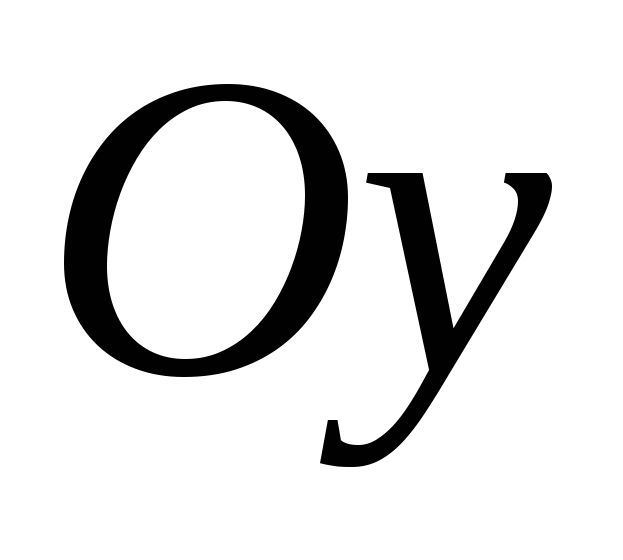в 2 раза и получаем требуемый график.
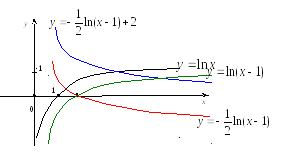
б)
Построить график функции
.
Решение.
1)
строим график
;
2)
сдвигаем его влево по оси
на 1, получаем график функции
;
3)
сжимаем график
вдоль оси
в
2 раза и строим симметричный ему
относительно оси
,
получаем график
;
4)
поднимаем график функции
по оси Оy
вверх на две единицы, получаем искомый
график.
2. Предел последовательности. Предел функции. Теоремы о пределах
Предел последовательности
Определение.
Число a
называется пределом
числовой последовательности
,
если для любого, сколь угодно малого,
наперед заданного числа
существует такой номер
,
что для всех
выполняется неравенство:
. (1)
Обозначение:
Предел функции
Число
А
называется пределом
функции
при
(
определена в некоторой окрестности т.
),
если для любого
существует такое
(
),
что как только
выполняется неравенство
. (2)
Теоремы о пределах
1.
Если существует
(
),
то
2.
Если существует
и
,
то
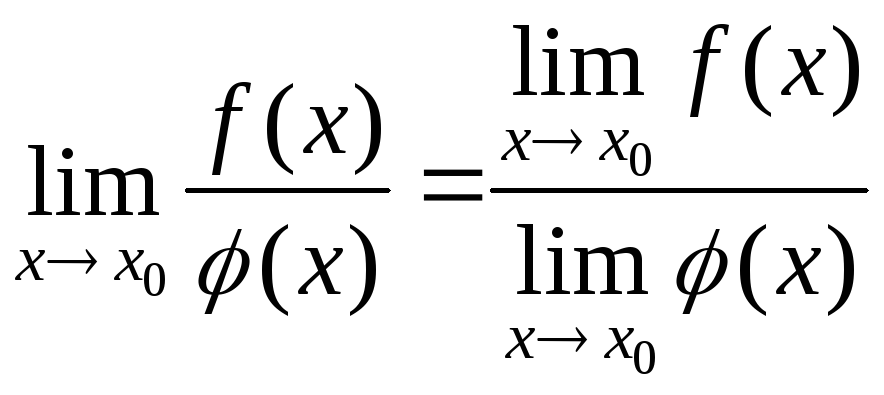
Таким
образом, для вычисления
необходимо в
подставить значение
.
Если
условия этих теорем не выполняется то
могут возникнуть неопределенности.
Простейшие из них вида
,
и
раскрываются с помощью алгебраических
преобразований
.
АЗ-2
1.
Доказать, что последовательность
имеет предел
.
(Указать
).
Ответ:
.
Найти пределы указанных функций.
|
2.
|
13.
|
|
3.
|
14.
|
|
4.
|
15.
|
|
5.
6.
|
16.
17.
|
|
7.
|
18.
|
|
8.
|
19.
|
|
9.
|
20.
|
|
10.
|
21.
|
|
11.
|
22.
|
|
12.
|
|
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
ИДЗ-2
Задание
1. Доказать,
что
(Указать
)
|
1.
|
|
16.
|
|
|
2.
|
|
17.
|
|
|
3.
|
|
18.
|
|
|
4.
|
|
19.
|
|
|
5.
|
|
20.
|
|
|
6.
|
|
21.
|
|
|
7.
|
|
22.
|
|
|
8.
|
|
23.
|
|
|
9.
|
|
24.
|
|
|
10.
|
|
25.
|
|
|
11.
|
|
26.
|
|
|
12.
|
|
27.
|
|
|
13.
|
|
28.
|
|
|
14.
|
|
29.
|
|
|
15.
|
|
30.
|
|
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.
Задание 2. Вычислить пределы указанных функций
|
Вариант 1 |
Вариант 2 |
|
1.
|
1.
|
|
2.
|
2.
|
|
3.
|
3.
|
|
4.
|
4.
|
|
5.
|
5.
|
|
6.
|
6.
|
|
7.
|
7.
|
|
8.
|
8.
|
|
9.
|
9.
|
|
10.
|
10.
|
|
11.
|
11.
|
|
Вариант 3 |
Вариант 4 |
|
1.
|
1.
|
|
2.
|
2.
|
|
3.
|
3.
|
|
4.
|
4.
|
|
5.
|
5.
|
|
6.
|
6.
|
|
7.
|
7.
|
|
8.
|
8.
|
|
9.
|
9.
|
|
10.
|
10.
|
|
11.
|
11.
|
|
Вариант 5 |
Вариант 6 |
|
1.
|
1.
|
|
2.
|
2.
|
|
3.
|
3.
|
|
4.
|
4.
|
|
5.
|
5.
|
|
6.
|
6.
|
|
7.
|
7.
|
|
8.
|
8.
|
|
9.
|
9.
|
|
10.
|
10.
|
|
11.
|
11.
|
|
Вариант 7 |
Вариант 8 |
|
1.
|
1.
|
|
2.
|
2.
|
|
3.
|
3.
|
|
4.
|
4.
|
|
5.
|
5.
|
|
6.
|
6.
|
|
7.
|
7.
|
|
8.
|
8.
|
|
9.
|
9.
|
|
10.
|
10.
|
|
11.
|
11.
|
|
Вариант 9 |
Вариант 10 |
|
1.
|
1.
|
|
2.
|
2.
|
|
3.
|
3.
|
|
4.
|
4.
|
|
5.
|
5.
|
|
6.
|
6.
|
|
7.
|
7.
|
|
8.
|
8.
|
|
9.
|
9.
|
|
10.
|
10.
|
|
11.
|
11.
|
|
Вариант 11 |
Вариант 12 |
|
1.
|
1.
|
|
2.
|
2.
|
|
3.
|
3.
|
|
4.
|
4.
|
|
5.
|
5.
|
|
6.
|
6.
|
|
7.
|
7.
|
|
8.
|
8.
|
|
9.
|
9.
|
|
10.
|
10.
|
|
11.
|
11.
|
|
Вариант 13 |
Вариант 14 |
|
1.
|
1.
|
|
2.
|
2.
|
|
3.
|
3.
|
|
4.
|
4.
|
|
5.
|
5.
|
|
6.
|
6.
|
|
7.
|
7.
|
|
8.
|
8.
|
|
9.
|
9.
|
|
10.
|
10.
|
|
11.
|
11.
|
|
Вариант 15 |
Вариант 16 |
|
1.
|
1.
|
|
2.
|
2.
|
|
3.
|
3.
|
|
4.
|
4.
|
|
5.
|
5.
|
|
6.
|
6.
|
|
7.
|
7.
|
|
8.
|
8.
|
|
9.
|
9.
|
|
10.
|
10.
|
|
11.
|
11.
|
|
Вариант 17 |
Вариант 18 |
|
1.
|
1.
|
|
2.
|
2.
|
|
3.
|
3.
|
|
4.
|
4.
|
|
5.
|
5.
|
|
6.
|
6.
|
|
7.
|
7.
|
|
8.
|
8.
|
|
9.
|
9.
|
|
10.
|
10.
|
|
11.
|
11.
|
|
Вариант 19 |
Вариант 20 |
|
1.
|
1.
|
|
2.
|
2.
|
|
3.
|
3.
|
|
4.
|
4.
|
|
5.
|
5.
|
|
6.
|
6.
|
|
7.
|
7.
|
|
8.
|
8.
|
|
9.
|
9.
|
|
10.
|
10.
|
|
11.
|
11.
|
|
Вариант 21 |
Вариант 22 |
|
1.
|
1.
|
|
2.
|
2.
|
|
3.
|
3.
|
|
4.
|
4.
|
|
5.
|
5.
|
|
6.
|
6.
|
|
7.
|
7.
|
|
8.
|
8.
|
|
9.
|
9.
|
|
10.
|
10.
|
|
11.
|
11.
|
|
Вариант 23 |
Вариант 24 |
|
1.
|
1.
|
|
2.
|
2.
|
|
3.
|
3.
|
|
4.
|
4.
|
|
5.
|
5.
|
|
6.
|
6.
|
|
7.
|
7.
|
|
8.
|
8.
|
|
9.
|
9.
|
|
10.
|
10.
|
|
11.
|
11.
|
|
Вариант 25 |
Вариант 26 |
|
1.
|
1.
|
|
2.
|
2.
|
|
3.
|
3.
|
|
4.
|
4.
|
|
5.
|
5.
|
|
6.
|
6.
|
|
7.
|
7.
|
|
8.
|
8.
|
|
9.
|
9.
|
|
10.
|
10.
|
|
11.
|
11.
|
|
Вариант 27 |
Вариант 28 |
|
1.
|
1.
|
|
2.
|
2.
|
|
3.
|
3.
|
|
4.
|
4.
|
|
5.
|
5.
|
|
6.
|
6.
|
|
7.
|
7.
|
|
8.
|
8.
|
|
9.
|
9.
|
|
10.
|
10.
|
|
11.
|
11.
|
|
Вариант 29 |
Вариант 30 |
|
1.
|
1.
|
|
2.
|
2.
|
|
3.
|
3.
|
|
4.
|
4.
|
|
5.
|
5.
|
|
6.
|
6.
|
|
7.
|
7.
|
|
8.
|
8.
|
|
9.
|
9.
|
|
10.
|
10.
|
|
11.
|
11.
|
Задание 3.* Вычислить пределы числовых последовательностей (функций)
|
Вариант 1 |
Вариант 2 |
|
|
1.
|
1.
|
|
|
2.
|
2.
|
|
|
3.
|
3.
|
|
|
4.
|
4.
|
|
|
5.
|
5.
|
|
|
Вариант 3 |
Вариант 4 |
|
|
1.
|
1.
|
|
|
2.
|
2.
|
|
|
3.
|
3.
|
|
|
4.
|
4.
|
|
|
5.
|
5.
|
|
|
Вариант 5 |
Вариант 6 |
|
|
1.
|
1.
|
|
|
2.
|
2.
|
|
|
3.
|
3.
|
|
|
4.
|
4.
|
|
|
5.
|
5.
|
|
|
Вариант 7 |
Вариант 8 |
|
|
1.
|
1.
|
|
|
2.
|
2.
|
|
|
3.
|
3.
|
|
|
4.
|
4.
|
|
|
5.
|
5.
|
|
|
Вариант 9 |
Вариант 10 |
|
|
1.
|
1.
|
|
|
2.
|
2.
|
|
|
3.
|
3.
|
|
|
4.
|
4.
|
|
|
5.
|
5.
|
|
|
Вариант 11 |
Вариант 12 |
|
|
1.
|
1.
|
|
|
2.
|
2.
|
|
|
3.
|
3.
|
|
|
4.
|
4.
|
|
|
5.
|
5.
|
|
|
Вариант 13 |
Вариант 14 |
|
|
1.
|
1.
|
|
|
2.
|
2.
|
|
|
3.
|
3.
|
|
|
4.
|
4.
|
|
|
5.
|
5.
|
|
|
Вариант 15 |
Вариант 16 |
|
|
1.
|
1.
|
|
|
2.
|
2.
|
|
|
3.
|
3.
|
|
|
4.
|
4.
|
|
|
5.
|
5.
|
|
|
Вариант 17 |
Вариант 18 |
|
|
1.
|
1.
|
|
|
2.
|
2.
|
|
|
3.
|
3.
|
|
|
4.
|
4.
|
|
|
5.
|
5.
|
|
|
Вариант 19 |
Вариант 20 |
|
|
1.
|
1.
|
|
|
2.
|
2.
|
|
|
3.
|
3.
|
|
|
4.
|
4.
|
|
|
5.
|
5.
|
|
|
Вариант 21 |
Вариант 22 |
|
|
1.
|
1.
|
|
|
2.
|
2.
|
|
|
3.
|
3.
|
|
|
4.
|
4.
|
|
|
5.
|
5.
|
|
|
Вариант 23 |
Вариант 24 |
|
|
1.
|
1.
|
|
|
2.
|
2.
|
|
|
3.
|
3.
|
|
|
4.
|
4.
|
|
|
5.
|
5.
|
|
|
Вариант 25 |
Вариант 26 |
|
|
1.
|
1.
|
|
|
2.
|
2.
|
|
|
3.
|
3.
|
|
|
4.
|
4.
|
|
|
5.
|
5.
|
|
|
Вариант 27 |
Вариант 28 |
|
|
1.
|
1.
|
|
|
2.
|
2.
|
|
|
3.
|
3.
|
|
|
4.
|
4.
|
|
|
5.
|
5.
|
|
|
Вариант 29 |
Вариант 30 |
|
|
1.
|
1.
|
|
|
2.
|
2.
|
|
|
3.
|
3.
|
|
|
4.
|
4.
|
|
|
5.
|
5.
|
|
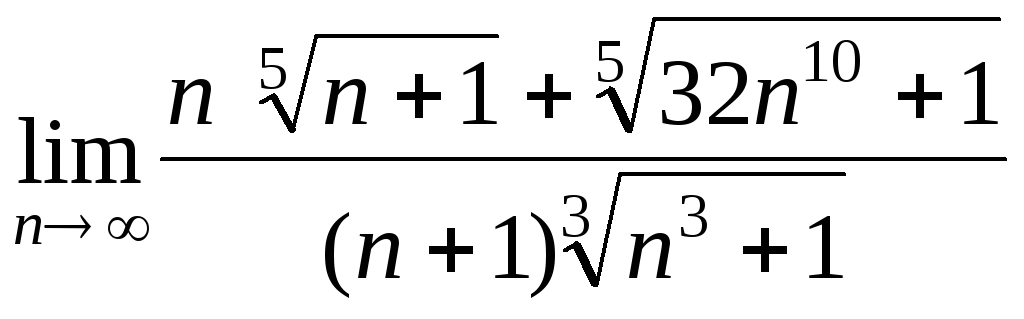